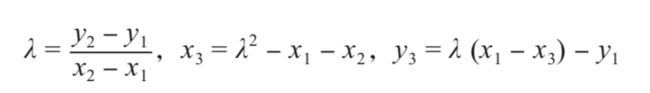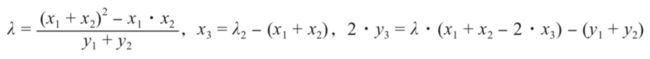比特币安全性究竟如何?

 

编辑 | kou

 

区块链安全问题，关系到每个人，当然也包括你。

 

自 the DAO 事件发生以来，区块链安全问题层出不穷，愈演愈烈，一个很简单的代码漏洞，就会威胁到你自身数字资产的安全，让你倾家荡产。

 

近期 EOS 游戏的体验感也十分差劲，这与一些黑客脱不了关系，但总体来说，终归是你写的代码自身就不安全...

 

◆ ◆ ◆  ◆ ◆

 

主流区块链安全属性分析

 

区块链安全是信息安全的一个应用领域。

 

信息安全是指保证信息系统中的数据在存取、处理、传输和服务过程中的保密性、完整性和可用性，保证信息系统本身能连续、可靠、正常地运行，并且在遭到破坏后能够迅速地恢复正常使用。

 

在世界各地都出现过信息系统被非授权用户非法入侵的事件，使得系统中存储的数据、信息的完整性、保密性受到了严重威胁。这类入侵行为可能导致信息由于被破坏而不能继续使用，或是使得系统中有价值和秘密的信息被非法窃取、篡改、伪造或删除，从而给使用者造成巨大的经济损失。

 

另外，信息系统还容易遭受各种不可抗拒的自然灾害的破坏，这同样需要我们给予足够的重视。

 

目前，区块链的应用已经得到了广泛的讨论，而对于区块链技术的安全属性分析相对较少。本文将以 3 个典型的区块链应用——比特币、以太币、Zcash 为例对此展开分析。

 

比特币

 

比特币(BitCoin)是一种 P2P 形式的数字货币。点对点的传输意味着一个去中心化的 支付系统。比特币不依靠特定货币机构发行，而是依据特定算法，通过大量的计算产生。比特币经济使用整个 P2P 网络中由众多节点构成的分布式数据库来确认并记录所有的交易行为，并使用密码学的设计来确保货币流通中各个环节的安全性。

 

比特币的核心钱包(Bitcoin Core)可以在 https://github.com/bitcoin/bitcoin.git 下载，在此分析的是 0.15.1 版本。在编译之前，需要先安装 libssl、libboost、libevent 等依赖库。如果出现问题，可在 doc 文件夹下查看 build → *.md 文件。Linux 中的安装步骤如下。

 

1)autogen.sh；

2)./conf igure；

3)make；

4)make install。

 

安装后会在 src 文件夹中生成 bitcoind、bitcoin-cli、bitcoin-tx 3 个可执行文件。

 

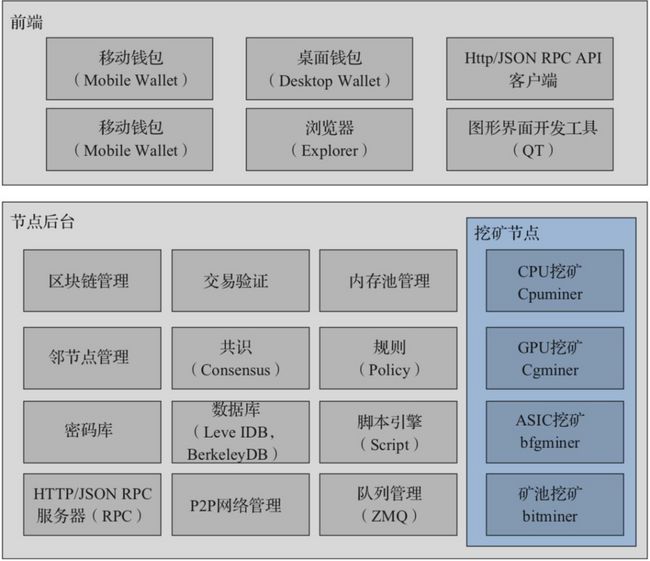
从最初的比特币源代码可以看出，比特币系统没有明确的模块划分。下图所示是根据目前的代码情况勾画的比特币架构。

 

比特币架构

 

比特币源代码 bitcoin 中含有两个与密码算法相关的文件夹:secp256k1 和 crypto。

 

secp256k1 文件夹中包含了一个椭圆曲线数字签名(Elliptic Curve Digital Signature Acgorithm，ECDSA)，选用的椭圆曲线是 E (Fp): y2 = x3 + 7，其中 p = 2256 - 232 - 29 - 28 - 27- 26 - 24 - 1。这条曲线是由专注于椭圆曲线密码技术的 Certicom 公司在 SECG 标准中推荐 的。在比特币系统中，ECDSA 主要对交易信息进行签名。如果签名后，再对交易信息修改， 就可以通过验证签名来检测出来。

 

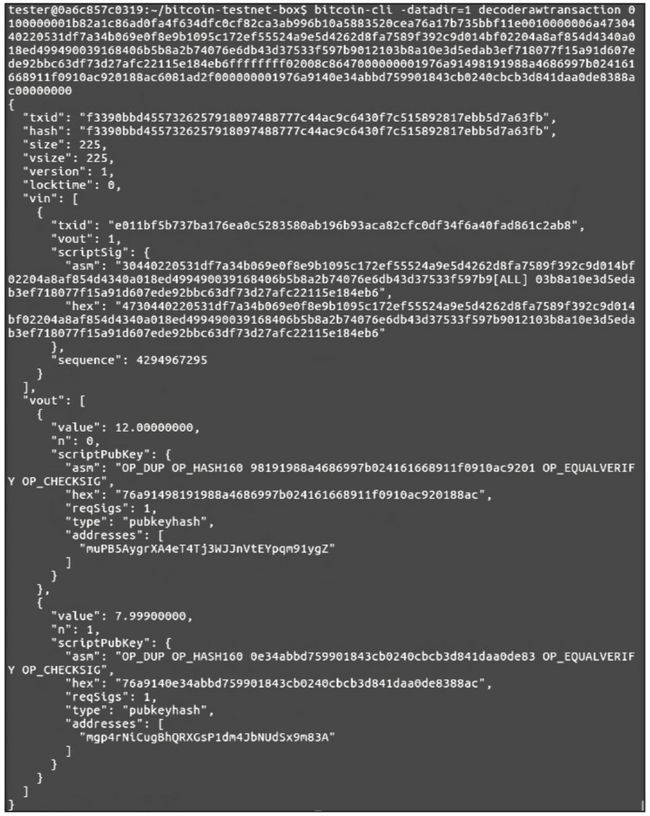
假设用户 A 和用户 B 进行交易，用户 A 支付 12 个比特币到用户 B 的地址 muPB5Aygr XA4eT4Tj3WJJnVtEYpqm91ygZ，生成的交易原始数据如下。

 

使用 ECDSA 对这段数据签名得到:

 

解析这段数据，结果如下图所示。

解析后的交易信息

 

攻击者 C 截取交易信息后，把交易的接收地址改为自己的地址：

mvXf3anW6XizkRB- AFfFMMt jwJr 2sL4ZuBd。

 

修改后的交易原始数据为:

 

 

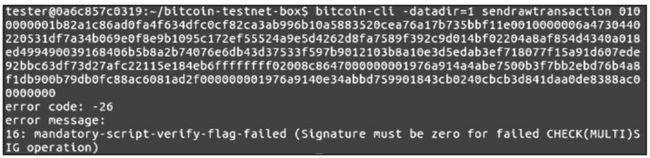
其中加粗的字符对应修改后的地址。由于 ECDSA 的签名需要用户 A 的私钥，所以攻击者 C 无法伪造数字签名。此时攻击者再转发交易，将返回验签错误，如下图所示。

验证交易

 

密码设备在运算过程中会泄漏各种物理信息，如功耗、电磁辐射、时间、声音、可见光等。利用这些物理信息也是可以破解出秘密信息的，这种攻击方法称为侧信道攻击。这类新型攻击的有效性远高于密码分析的数学方法，因此给密码设备带来了严重的威胁。

 

1996年美国科学家 Kocher 首先发现针对密码芯片的时间攻击法。该方法通过对密码芯片运算过程中执行时间信息的采集，结合密码算法的内部实现，证实了算法指令和执行时间存在相关性，从而推测出密钥信息。

 

1999 年，Kocher 等人又提出了利用功耗采集数据去分析密码电路中的秘密信息，并提出了简单功耗分析(SPA)和差分功耗分析(DPA)的方法。

 

比特币的 ECDSA 算法在实现过程中考虑了防御侧信道攻击。比如 ECDSA 会调用点乘算法，而点乘算法又会调用点加、倍点运算。通常情况下，椭圆曲线点加、倍点的计算公式 是不一样的。设点 P = (x1, y1), Q = (x2, y2)，曲线 y2 = x3 + b 的点加公式为:

 

倍点公式为:

 

为了防御旁路分析，程序员参考了相关文献中的方法，使用相同的公式计算点加和倍点:

 

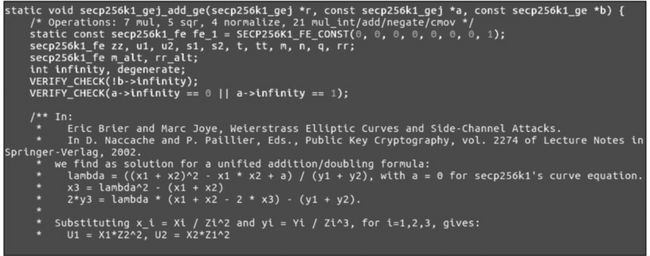
下图所示是比特币系统中的点加、倍点程序的部分截屏。

 

点加、倍点函数

 

crypto 文件夹主要处理地址，采用了 SHA-256 和 RIMEMD-160 两个 Hash 函数。

 

同时，crypto 还提供了 Hash 函数 SHA-1。强烈建议不要使用这个函数，因为它已经不再安全。

 

国家密码管理局在 2017 年 4 月 3 日发布了《关于使用 SHA-1 密码算法的风险提 示》:近期，SHA-1 杂凑密码算法碰撞攻击实例公布，对 SHA-1 算法的攻击从理论变为现实， 继续使用 SHA-1 算法存在重大安全风险。

 

比特币核心钱包(Bitcoin Core)是官方发布的用于管理比特币私钥的客户端。拥有比特 币地址的私钥代表拥有对应的比特币的控制权。为了防止非授权用户使用比特币，以及防止 比特币被盗，应该对比特币钱包进行加密。加密比特币钱包的命令为:

./bitcoin-cli encryptwallet

 

加密完成后，需要重启客户端来加载加密后的钱包。进行交易前，需要先把 passphrase存入内存，以解密钱包。

./bitcoin-cli walletpassphrase

 

timeout 是指该口令在内存中有效的时间，计时单位是秒。超过这个时间后，需要重新调用这条命令。为了安全起见，timeout 的值不要设置得很长，尽量做到每次交易都要输入 一次口令。

 

私钥一旦丢失将无法恢复，也就意味着比特币的丢失。因此，备份好钱包非常重要。 备份钱包的命令为:

./bitcoin-cli backupwallet

 

这条命令把 wallet.dat 文件复制到目标文件夹中。为了安全起见，wallet.dat 应该备份到安全的地方，比如离线的 U 盘。在多个地方安全地保管钱包文件可防止意外情况发生的时候恢复。

 

为了保证资金的安全性。还可以使用冷存储，即把私钥存储在一台永不上线的计算机 上，交易时使用离线签名。具体步骤为:

 

首先在离线计算机上生成钱包 wallet.dat，并生 成比特币地址，然后删除这个钱包中的密钥，再把这个没有密钥的钱包复制到在线计算机 上。

 

当冷存储比特币时，只需把比特币转账到该钱包中的地址;当需要使用冷存储的比特币时，需要首先用在线计算机生成未签名的原始交易 RawTransaction，然后把该原始交易放到离线计算机上进行签名，最后使用在线计算机广播签名后的交易。

 

但是，比特币官方钱包Bitcoin Core 0.14.2 版本还无法删除 wallet.dat 中的密钥，所以还不支持冷存储。可以使用其他钱包进行冷存储，比如 armory 钱包 https://www.bitcoinarmory.com/。

 

Bitcoin Core 钱包提供多重签名，可以通过 createmultisig 命令来生成带有多重签名的地 址。下面演示如何生成一个 3 取 2 的多重签名地址，即有 3 个管理员，只需任意两个完成签名，就可以进行交易。具体过程如下:

 

先生成 3 个管理员的密钥。为了达到安全级别 II，建议这 3 组密钥在不同地方生成和存储，以便防范火灾、洪水、地震等风险。

 

通过 ./bitcoin-cli getnewaddress 得到 3 个地址:

• mumwWHRHzXaS2fCYB6MrjSg2runDwxa4ZQ

• n3LoBtt2mmcTk5dchm7Ba4RbU7pVpE1q43

• mrEmwE8r9Wq9sNefGWbpyqP5uSZgscQDr4

 

利用 ./bitcoin-cli dumpprivkey 获得 3 个私钥:

• cPzefVCmScBJWA2cQ7ngHqwWpMzypwFfvxrw2ykPias19moC9Ssg

• cTuYQj2oumFLf4rWJHqJRxw9K3tsZoBH8488KaUbXWNz1jV5tPgj

• cUW3QnvoebJVSkJbvVEtJTBFYzsy6z1Pu5yQXfpF8HVTJkrqfAWk
   

再利用 ./bitcoin-cli validateaddress 获得对应的 3 个公钥:

• 039f03c79800b56825dcafbb6c85c1f84964006a337c0d47b3a1bef7a5d835d897

• 02c870602256f042039aec374a1164e9168128ada4ddad498c02a50fdbf39e375c

• 03fd9030258cdf1001335db26ef9fc7a3ae3563ff8b1356afeb81dd95b81bfdf56 

 

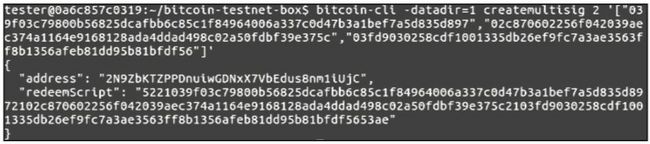
然后生成多重签名地址，如下图所示。

 

 

生成多重签名地址

 

生成的地址为：

2N9ZbKTZPPDnuiwGDNxX7VbEdus8nm1iUjC。

 

再添加多重签名地址到钱包:

 

可以通过 ./bitcoin-cli getaddressesbyaccount 来查看是否已经将地址添加到钱包。接下来，演示如何使用这个多重签名地址进行交易。

 

首先使用命令 ./bitcoin-cli sendtoaddress 给多重签名地址 2N9Z- bKTZPPDnuiwGDNxX7VbEdus8nm1iUjC 转入 1 个比特币。然后创建一笔交易，把 0.7 个比 特币从这个地址转出到 mvXf3anW6XizkRBAFfFMMtjwJr2sL4ZuBd。

 

./bitcoin-cli createrawtran- saction [{"txid":txid,"vout":n},...] {address:amount,...} 

生成的交易原始数据为:

 

 

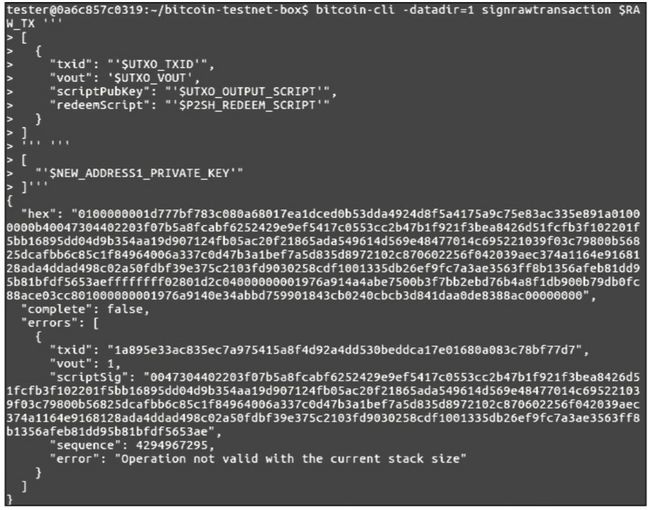
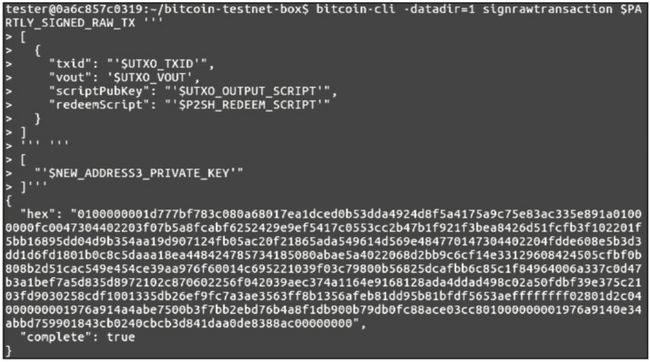
使用第一个地址对应的私钥进行签名，如下图所示。

第一次签名

 

可以发现，第一次签名后，complete 字段是 false，因为创建的地址 2N9ZbKT- ZPPDnuiwGDNxX7VbEdus8nm1iUjC 需要至少两次签名(这样可以提高钱包中资产的安全性)。使用第二个地址对应的私钥进行签名，图下所示。

 

第二次签名

 

此时，complete 字段为 true，表明交易创建完成，可以使用 ./bitcoin-cli sendrawtransaction 发送了。在真实的比特币网络中，等待 6 次确认后，就可以通过 ./bitcoin-cli- getreceivedbyaddress 来查看是否收到了转入金额。

 

比 特 币 密 钥 生 成 时 会 调 用 bitcoin/src/random.cpp 中 的 GetStrongRandBytes 函 数 来 生 成随机数。这个函数会先调用 OpenSSL 中的 GetRandBytes 函数生成 256bit 随机数;再调 用 GetOSRand 函数生成 256bit 随机数;随后如果能获取，就会调用硬件的随机数生成函 数 GetHWRand 来生成 256bit 随机数。

 

接着把这 3 部分串接在一起，使用 Hash 函数生成 一个 512bit 的随机数。最后取出前 256bit 作为密钥。为了测试比特币密钥的随机性，调用GetStrongRandBytes 函数生成了 1200 个长度为 106 的随机数比特流，然后使用 NIST STS 的 随机数测试套件对这个比特流进行了测试。

 

NIST STS 的随机数测试套件一共有 15 项测试: 单比特频数检测、块内频数检测、累加和检测、游程检测、块内最大“1”游程检测、矩阵 秩检测、离散傅里叶检测、非周期模块匹配检测、重叠模块匹配检测、通用统计检测、近似熵检测、随机游动检测、随机游动变体检测、序列检测、线性复杂性检测。

 

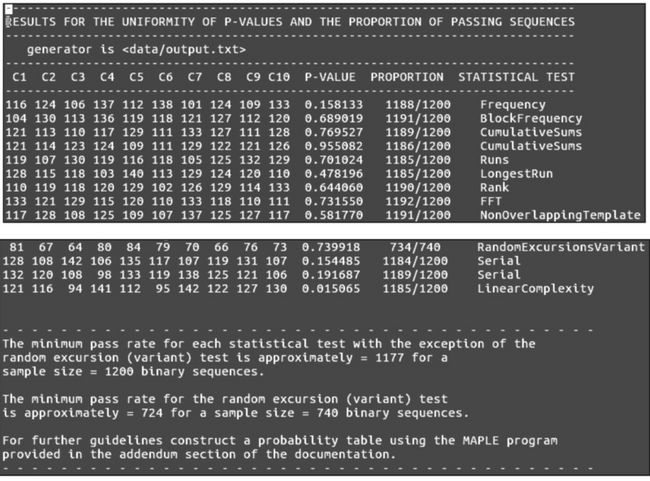
测试结果如下图所示。

GetStrongRandBytes 生成的随机数测试

 

由于测试结果很长，在此只截取了前后两部分。从中可以看出，绝大部分比特流都通 过了测试，仅有极少数比特流没有通过。

 

比如 Frequency 测试中，在 1200 个比特流中通过 了 1188 个，而底部的测试结论已经说明“在 1200 个中只要通过 1177 个就表明这一项测试通过”。只有 random excursion(variant)测试例外，只要在 740 个样本中，大于 724 个通过就行了。

从以上测试分析可知，GetStrongRandBytes 生成的随机数通过了 NIST STS 的所有

15 项测试。所以，比特币中的密钥是一个足够随机的数。

 

推荐阅读

• 还有34天18年就过完了, 收好这份2019区块链行业指南

• 这个女生说：弄懂本文前，你所知道的区块链可能都是错的

• 30k~65k, "寒冬季"人才依旧紧缺!  架构师、工程师、产品经理仍为招聘刚需, 赶紧来投吧！

• 高达 800 万次下载量的 npm 包被黑客篡改了代码，你的设备或正成为挖矿机

• 为什么面试完，总是让你回去等通知？

• “基因编辑婴儿”惹争议，你或许不知道机器学习在脱靶效应中的作用？

• 为什么宇航员要在太空用超级计算机？

• 炸了！刚写完这段代码，就被开除了…

 

长按识别二维码关注区块链大本营

内容转载请加 171075719，备注“转载”

商务合作请加 fengyan-1101