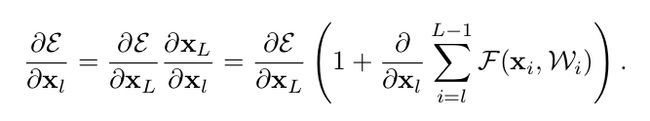【深度学习】经典神经网络 ResNet 论文解读

ResNet 是何凯明团队的作品，对应的论文 《Deep Residual Learning for Image Recognition》是 2016 CVPR 最佳论文。ResNet 的 Res 也是 Residual 的缩写，它的用意在于基于残差学习，让神经网络能够越来越深，准确率越来越高。

我们都知道，自 2012 年 AlexNet 在 ILSVRC 一战成名后，卷积神经网络便一发不可收拾，后续的各类竞赛中各种神经网络都大发异彩，除了更高的准确率之外，它们普遍的特征就是，网络的层级越来越深了。

这里会产生一个问题，那就是神经网络真的越深越好吗?

但至少有证据表明，情况不是这样的，如果神经网络越来越深，这个神经网络可能会出现退化(degradation) 的现象。这里说的退化是指网络层级加深后，训练的准确率却可能出现饱和的现象。

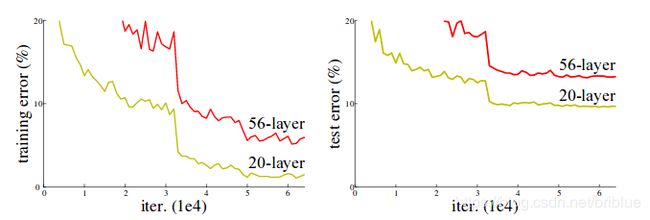
上面的图片指示的是在 CIFAR-10 这个小型的数据集上，56 层的神经网络的表现比不过 20 层的神经网络。也就是前面说的层数越深，网络却反而退化了。

如何构建更深层的网络？

前面提到的，当网络层次更深时，反而会出现退化的现象，那么有没有办法避免呢？

有一个解决方案是：

在一个的常规的比较浅的模型上添加新的层，而新的层是基于 identity mapping 的。

identity 是相同的意思，identity mapping 可以称为恒等变换，也就是输入与输出是相等的映射关系。

通俗来讲，就是在一个浅层的网络模型上进行改造，然后将新的模型与原来的浅层模型相比较，这里有个底线就是，改造后的模型至少不应该比原来的模型表现要差。因为新加的层可以让它的结果为 0，这样它就等同于原来的模型了。这个假设是 ResNet 的出发点。

那么如何做呢？

作者引入了 deep residual learning framework，也就是基于残差的深度学习框架，实际上是需要对常规的神经网络的改造。

我们都知道，目前流行的神经网络都可以看成是卷积层的堆叠，可以用栈来表示，我们就叫它卷积栈好了.

输入数据经过每个卷积层都会发生变化，产生新的 featuremap ，我们可以说数据在输入与输出间发生了映射，也就是 mapping。神经网络中的权重参数一个作用就是去拟合这种输入与输出之间的 mapping。

ResNet 准备从这一块动手，假设现在有一个栈的卷积层比如说 2 个卷积层堆叠，将当前这个栈的输入与后面的栈的输入之间的 mapping 称为 underlying mapping，现在的工作是企图替换它引入一种新的 mapping 关系，ResNet 称之为 residual mapping 去替换常规的 mapping 关系。

意思是与其让卷积栈直接拟合 underlying mapping，不如让它去拟合 residual mapping。而 residual mapping 和 underlying mapping 其实是有关联的。

将 underlyingmapping 标记为 $H(x)$

将经过堆叠的非线性层产生的 mapping 标记为 $F(x):=H(x)-x$

所以，最原始的 mapping 就被强制转换成 $F(x)+x$

然后，作者假设对 residual mapping 的优化要比常规的 underlying mapping 要简单和容易

而$F(x)+x$ 在实际的编码过程中，可以被一种叫做快捷连接的结构件来实现。

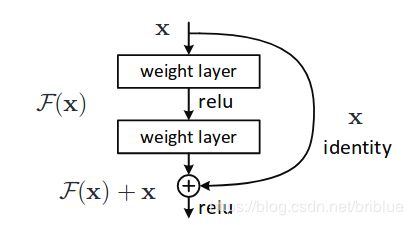
快捷连接通常会跳过 1 个或者多个层，在 ResNet 中快捷连接直接运用了 identity mapping，意思就是将一个卷积栈的输入直接与这个卷积栈的输出相加。

这样有什么好处呢？

1. 并没有增加新的参数
2. 整个网络也仍然可以由 SGD 进行训练。
3. 容易被通用的神经网络框架实现。

并且，$F(x)$ 表示残差，最理想的情况是 identity mapping 是最优的输出，那么让$F(x)$ 为 0 就好了，现实是$F(x)$不可能全为 0，那么这些多出来的东西就可以增强网络的表达能力。

而 ResNet 依靠成绩说话，它是 ILSVRC 2015 年图像分类冠军。而且 ResNet 的泛化变现也很卓越，在 ImageNet 目标检测、ImageNet 目标定位、COCO 目标检测、COCO 图像分割等竞赛中都取得了当年（2015）的冠军。

并且，ResNet 是当年 ImageNet 参赛模型中层级最深的模型，达到了 152层。

这些证据证明了 ResNet 加深网络后，性能比其他的模型更突出。

Deep Residual Learning

Residual Learning 的理论依据

我们可以将焦点放在 $H(x)$ 上。

理论上有一种假设，多层卷积的参数可以近似地估计很复杂的函数表达公式的值，那么多层卷积也肯定可以近似地估计 $H(x)-x$ 这种残差公式。

所以与其让卷积栈去近似的估计 $H(x)$,还不如让它去近似地估计 $F(x):=H(x)-x$, 而 $F(x)$就是残差。

作者假设的是，残差比原始的 mapping 更容易学习。

作者在他的另外一篇论文《Identity Mappings in Deep Residual Networks》中给出了详细的讨论。

一个残差单元，它的输入与输出的关系可以用下面的公式表达：
$$Yl=h(xl)+F(xl)$$
$$xl+1=f(Yl)$$

$l$ 代表层的意思，$xl$ 代表当前这个残差单元的信号输入，$xl+1$代表输出，同时也是神经网络下一层的输入。
$h(x)$代表的 identity mapping，$F(xl)$ 是这个单元的残差，$f(yl)$ 是 ReLU 激活函数。

我们先整理一下思路，神经网络训练过程中反向传播的梯度非常重要，如果梯度接近于 0 ，那么信号就无法反向传播了。

XL 代表任意的一个更深层次的输入，而 Xl 可以代表相对的比较浅的层次的输入,结合之前的公式，可以很容易递推得到上面的公司。

引用链式求导法则。

$\epsilon$ 代表的是 loss 方程

最激动人心的地方在于上面公式的括号部分，它是 1 加上某个值，只要这个值不恰好为 -1，那么梯度就不会为 0，也就是说从 XL 到 Xl 的梯度就可以一直传递下去，梯度能够有效传递，神经网络的训练过程才会更加高效。

网络结构

ResNet 的起始是从一个常规的比较浅的网络上探求加层的过程。

这个常规的比较浅的网络是大名鼎鼎的 VGG-19。

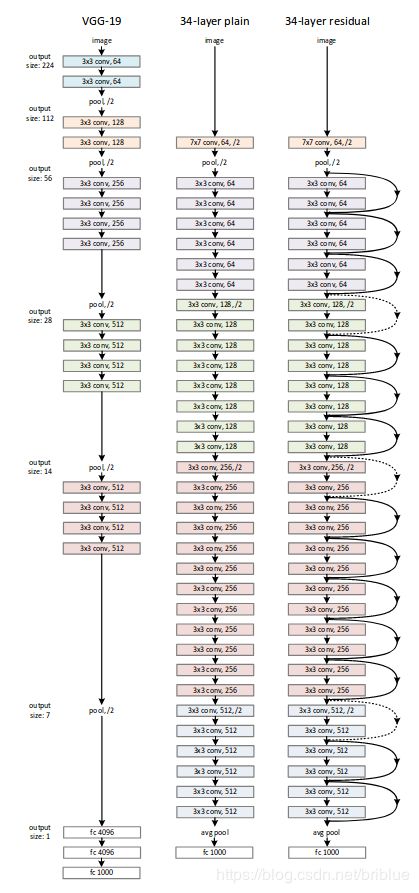
作者对 VGG-19 进行仿制与改造，得到了一个 34 层的 plain network，然后又在这个 34 层的 plain network 中插入快捷连接，最终形成了一个 34 层的 residual network。

我们回到这张图上面，$F(x)$ 要与 x 相加，那么它们的维度就需要一样。

而 ResNet 采用的是用 1x1 的卷积核去应对维度的变化，通过 1x1 的卷积核去对输入进行升维和降维。

1x1卷积核的意义可以参考

ResNet 作者做了大量的模型评估工作，网络的层数从 18 到 152 都有试验。

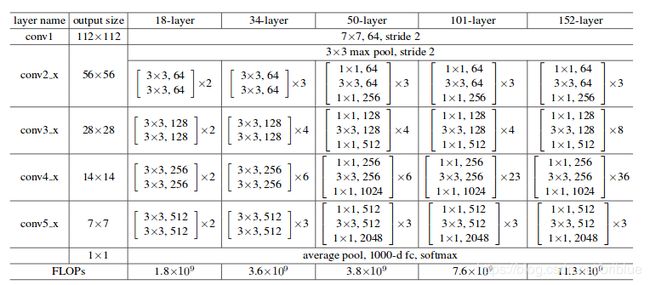
值得注意的是，从 50-layer 起，ResNet 采用了一种 bottleneck design 的手段。

1x1 的卷积核让整个残差单元变得更加细长，这也是 bottleneck 的含义，更重要的是参数减少了。

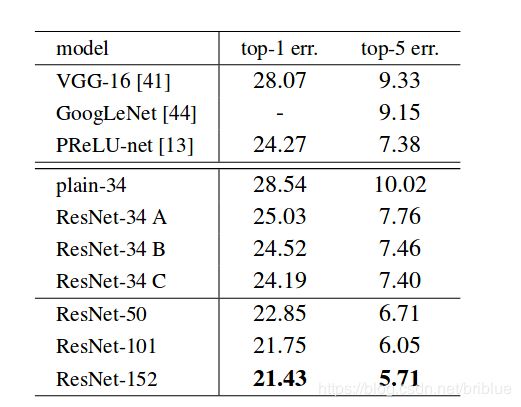
最终在 ImageNet 验证集上的表现也证明了 ResNet 比当时其他网络要强，并且 ResNet 本身层级越多准确率越高。

最后，为了证明 ResNet 的泛化能力，作者也在 CIFAR-10 数据集上做了测试和分析，ResNet 甚至做到了 1000 层以上。

这证明了基于残差学习可以让网络更深。

总结

1、ResNet 在当年大放异彩靠的是它优异的表现。
2、论文更多讲述的是经验，这些经验靠实验结果表现出了 ResNet 的高效，但后来的补充材料给出了理论依据，自此它才变得更加让人信服。
3、ResNet 并非横空出世，它是基于浅层网络的探索性的结果，就如 VGG 是在 AlexNet 的基础上探索得到的。
4、ResNet 验证了大量的结构，并且进行了大量的横向和纵向对比才得到的最理想的结果，这份细致和耐心值得我们每个人学习。