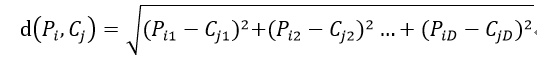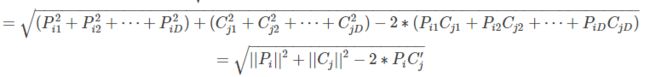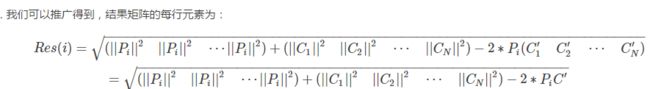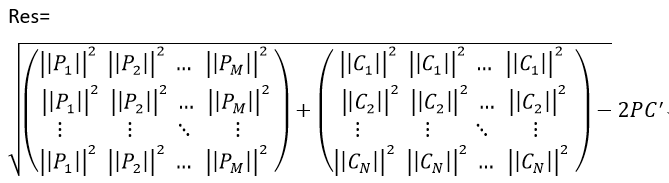运行cs231n课程中Assignment1中的示例代码

cs231n上的课程作业1，传送门：斯坦福大学深度学习与计算机视觉公开课作业1

因为我用的版本是python3.6.0，而示例代码似乎是python2版本的，于是遇到一些问题。

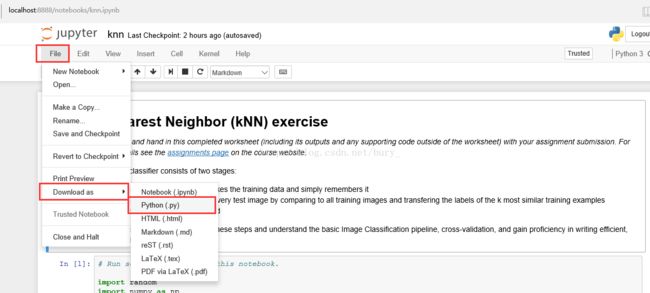
示例代码是ipynb格式的，打开方式：cmd下运行ipython notebook, 在浏览器中打开网页（如下），可以点击Upload按钮选择要打开的文件。

但是代码是一行一行的，怎么在spyder里面直接运行呢？

如图2点击保存为python格式的就可以在spyder里面打开了。

一运行发现报错了，原来数据集没有下载：

回头看作业页面的说明，原来说了要怎么下载的：

但是这个是Shell命令。（windows10上可以启用linux子系统）打开bash，输入命令，开始下载CIFAR-10 dataset：

运行代码的时候报了许多错，其中之一是pickle.load反序列化，

  File "E:\assignment1\cs231n\data_utils.py", line 9, in load_CIFAR_batch
    datadict = pickle.load(f)

UnicodeDecodeError: 'ascii' codec can't decode byte 0x8b in position 6: ordinal not in range(128)

查到别人的解答， 点击打开链接

with open(filename, 'rb') as f:
    datadict = pickle.load(f,encoding='iso-8859-1')

我们需要告诉pickle：how to convert python bytestring data to Python 3 strings，The default is to try and decode all string data as ASCII

填补代码说明：

1. 交叉验证选择最佳的K值

# In[ ]:


num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]

X_train_folds = []
y_train_folds = []
################################################################################
# TODO:                                                                        #
# Split up the training data into folds. After splitting, X_train_folds and    #
# y_train_folds should each be lists of length num_folds, where                #
# y_train_folds[i] is the label vector for the points in X_train_folds[i].     #
# Hint: Look up the numpy array_split function.                                #
################################################################################
X_train_folds=np.array_split(X_train,num_folds)
y_train_folds=np.array_split(y_train,num_folds)
################################################################################
#                                 END OF YOUR CODE                             #
################################################################################

# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}


################################################################################
# TODO:                                                                        #
# Perform k-fold cross validation to find the best value of k. For each        #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times,   #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all     #
# values of k in the k_to_accuracies dictionary.                               #
################################################################################
for k in k_choices:
    k_to_accuracies[k] = np.zeros(num_folds)
    for i in range(num_folds):
        Xtr = np.array(X_train_folds[:i] + X_train_folds[i+1:])#把训练集中的一块划为验证集
        ytr = np.array(y_train_folds[:i] + y_train_folds[i+1:])
        Xte = np.array(X_train_folds[i])
        yte = np.array(y_train_folds[i])     

        Xtr = np.reshape(Xtr, (X_train.shape[0]/ 5*4, -1))
        ytr = np.reshape(ytr, (y_train.shape[0]/ 5*4, -1))
        Xte = np.reshape(Xte, (X_train.shape[0] / 5, -1))
        yte = np.reshape(yte, (y_train.shape[0] / 5, -1))

        classifier.train(Xtr, ytr)
        yte_pred = classifier.predict(Xte, k)
        yte_pred = np.reshape(yte_pred, (yte_pred.shape[0], -1))
        num_correct = np.sum(yte_pred == yte)
        accuracy = float(num_correct) / len(yte)
        k_to_accuracies[k][i] = accuracy

        
################################################################################
#                                 END OF YOUR CODE                             #
################################################################################

# Print out the computed accuracies
for k in sorted(k_to_accuracies):
    for accuracy in k_to_accuracies[k]:
        print ('k = %d, accuracy = %f' % (k, accuracy))

这里使用的是交叉验证(cross-validation)去获取knn中的超参数K的最佳值，其基本思想是，将训练集划分为num_folds个块，循环地把其中的一块作为验证集，计算不同K值下载所有遍历的验证集上的准确率(num_folds个结果)的平均值作为该K值在训练集上的准确率，然后选择这个准确率最高的K值作为KNN中的K。

在这个试验中，num_folds的值为5，也就是把训练集分作了5块，这个操作是使用

np.array_split(X_train,num_folds)

然后再使用一个循环，其次数为num_folds次，每一次循环里选择其中一块作为验证集，然后把剩下的作为训练集，调用train函数训练（KNN并不训练，只是保存了训练数据），然后使用predict得到验证集的预测标签，判断预测标签和实际标签对应的正确率，作为该K值下该块验证集对应的准确率，运行结果如下：

k = 1, accuracy = 0.263000
k = 1, accuracy = 0.257000
k = 1, accuracy = 0.264000
k = 1, accuracy = 0.278000
k = 1, accuracy = 0.266000
k = 3, accuracy = 0.257000
k = 3, accuracy = 0.263000
k = 3, accuracy = 0.273000
k = 3, accuracy = 0.282000
k = 3, accuracy = 0.270000
k = 5, accuracy = 0.265000
k = 5, accuracy = 0.275000
k = 5, accuracy = 0.295000
k = 5, accuracy = 0.298000
k = 5, accuracy = 0.284000
k = 8, accuracy = 0.272000
k = 8, accuracy = 0.295000
k = 8, accuracy = 0.284000
k = 8, accuracy = 0.298000
k = 8, accuracy = 0.290000
k = 10, accuracy = 0.272000
k = 10, accuracy = 0.303000
k = 10, accuracy = 0.289000
k = 10, accuracy = 0.292000
k = 10, accuracy = 0.285000
k = 12, accuracy = 0.271000
k = 12, accuracy = 0.305000
k = 12, accuracy = 0.285000
k = 12, accuracy = 0.289000
k = 12, accuracy = 0.281000
k = 15, accuracy = 0.260000
k = 15, accuracy = 0.302000
k = 15, accuracy = 0.292000
k = 15, accuracy = 0.292000
k = 15, accuracy = 0.285000
k = 20, accuracy = 0.268000
k = 20, accuracy = 0.293000
k = 20, accuracy = 0.291000
k = 20, accuracy = 0.287000
k = 20, accuracy = 0.286000
k = 50, accuracy = 0.273000
k = 50, accuracy = 0.291000
k = 50, accuracy = 0.274000
k = 50, accuracy = 0.267000
k = 50, accuracy = 0.273000
k = 100, accuracy = 0.261000
k = 100, accuracy = 0.272000
k = 100, accuracy = 0.267000
k = 100, accuracy = 0.260000
k = 100, accuracy = 0.267000

准确率也都不算高，28%左右。

将每个K值对应的5个验证集上的准确率取平均值，绘制折线图如下：

可以看到，第5条竖线对应的均值达到了折线的顶峰，在K_choice里面第五个K值对应的是K=10，因此best_k的值应该改为10

# Based on the cross-validation results above, choose the best value for k,   
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = 10

classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)

# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print ('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

提示说最后的准确率应该比28%大，如果best_k取1时候，运行结果的准确率是27%左右，当把K改为10以后，准确率是：

Got 144 / 500 correct => accuracy: 0.288000

而没有使用交叉验证时候，指定K=1和K=5时候的准确率分别为27%和29%（ 这里没弄明白为什么交叉验证选出的K=10在测试集上的表现不如动手指定的k=5，可能因为选用的训练集并不是全部训练集）

Got 137 / 500 correct => accuracy: 0.274000 #k=1
Got 145 / 500 correct => accuracy: 0.290000 #k=5

2.使用欧式距离计算测试数据和训练数据的距离矩阵，三种方法，一种使用两层循环，二种使用一层循环，最后一种需要用到更多的数学知识和向量化处理，不使用循环进行计算：

def compute_distances_two_loops(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using a nested loop over both the training data and the 
    test data.

    Inputs:
    - X: A numpy array of shape (num_test, D) containing test data.

    Returns:
    - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
      is the Euclidean distance between the ith test point and the jth training
      point.
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in range(num_test):
      for j in range(num_train):
        #####################################################################
        # TODO:                                                             #
        # Compute the l2 distance between the ith test point and the jth    #
        # training point, and store the result in dists[i, j]. You should   #
        # not use a loop over dimension.                                    #
        #####################################################################
        dists[i,j]=np.sqrt(np.sum(np.square(self.X_train[j,:]-X[i,:])))
        #####################################################################
        #                       END OF YOUR CODE                            #
        #####################################################################
    return dists

  def compute_distances_one_loop(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using a single loop over the test data.

    Input / Output: Same as compute_distances_two_loops
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in range(num_test):
      #######################################################################
      # TODO:                                                               #
      # Compute the l2 distance between the ith test point and all training #
      # points, and store the result in dists[i, :].                        #
      #######################################################################
      dists[i,:] = np.sqrt(np.sum(np.square(self.X_train-X[i,:]),axis = 1))
      #np.square是针对每个元素的平方方法
      #######################################################################
      #                         END OF YOUR CODE                            #
      #######################################################################
    return dists

  def compute_distances_no_loops(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using no explicit loops.

    Input / Output: Same as compute_distances_two_loops
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train)) 
    #########################################################################
    # TODO:                                                                 #
    # Compute the l2 distance between all test points and all training      #
    # points without using any explicit loops, and store the result in      #
    # dists.                                                                #
    #                                                                       #
    # You should implement this function using only basic array operations; #
    # in particular you should not use functions from scipy.                #
    #                                                                       #
    # HINT: Try to formulate the l2 distance using matrix multiplication    #
    #       and two broadcast sums.                                         #
    #########################################################################
    dists = np.multiply(np.dot(X,self.X_train.T),-2) 
    sq1 = np.sum(np.square(X),axis=1,keepdims = True) 
    sq2 = np.sum(np.square(self.X_train),axis=1) 
    dists = np.add(dists,sq1) 
    dists = np.add(dists,sq2) 
    dists = np.sqrt(dists)
    #########################################################################
    #                         END OF YOUR CODE                              #
    #########################################################################
    return dists

第一种执行的时间效率最低的是使用两层循环，计算每个测试向量和每个训练向量的向量差，然后使用np.square()计算求得每个元素的平方（也可以使用点乘的方式： np.dot(X[i] - self.X_train[j], X[i] - self.X_train[j])），使用np.sum()计算元素平方的和，最后开方求得的就是该测试向量和训练向量的欧式距离，所有遍历下来需要计算500*5000次，也就是测试数据集的行数乘以训练数据集的行数。

5000行的3072维训练数据，500行的3072维测试数据，计算的时间花销是57秒左右：

Two loop version took 57.858908 seconds

第二种方法，使用一层循环，遍历每个测试向量，直接计算每个测试向量(1*3072)和所有训练向量(5000*3072)的差，得到一个5000*3072的矩阵，然后使用np.square(X)计算每个元素的平方，再使用np.sum(np.square(self.X_train-X[i,:]),axis = 1)计算每行所有列的元素平方的和，再开方得到一个5000*1的向量，以横向量形式保存在结果数组的一行 中，表示的是该测试向量和所有训练向量的欧式距离，最后得到的就是500*5000的一个结果，也就是测试数据集的行数乘以训练数据集的行数。

使用一层循环的时间开销是使用两层循环的两倍，大约106秒：

 One loop version took 106.198080 seconds

最后一种方式不使用循环，但是需要用到一点推理归纳：

我们先来计算一下 Pi 和 Cj 之间的距离 

因此，结果矩阵的表示形式为：

换成python代码就是:

      dists = np.multiply(np.dot(X,self.X_train.T),-2)  #维度是(500,5000)
    sq1 = np.sum(np.square(X),axis=1,keepdims = True)  #维度是(500,1)
    sq2 = np.sum(np.square(self.X_train),axis=1)     #维度是(5000,)没有保持维度，也不能保持维度
    dists = np.add(dists,sq1)                  #维度是(500,5000)
    dists = np.add(dists,sq2) 
    dists = np.sqrt(dists)

值得注意的是代码中先计算了最后一部分2PC'，此时数据维度是500*5000，然后计算测试数据和训练数据的元素平方，但是训练数据不能保持维度，最后使用np.add函数对两个向量和前面的矩阵进行加法，维度不变，依然是500*5000.