图像处理中的旋转、平移、缩放——仿射变换的原理和优化

仿射变换的原理

在条形码识别软件中有图像预览的功能。有时预览的图像需要进行转置（旋转180度或者90度）、缩放、镜像（左右反转）等操作。OpenCV提供了相应的函数进行以上操作。例如：
转置：cv::WarpAffine()
缩放：cv::resize()
镜像：cv::remap()
如果同时要转置，缩放和镜像，就需要进行三次图像运算。其实以上三个操作都是同一类型的变化，称作放射变化。可以把这3次图像运算合并成一次，从而优化运算时间。如何合并这三次运算，需要从仿射变换的原理说起。

举个例子，我们需要对以下图像（蓝色）顺时针旋转90度（橙色），可以这么做：假设原来的图像宽w高h

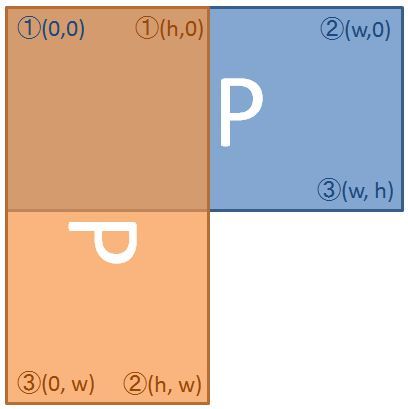
(1) 创建宽h高w内存区域存放新图像；
(2) 逐一把原图像中的像素(x0,y0)搬到新图像的对应像素(x1,y1)
例如原图像的左上角点①(0,0)被搬到新图像的右上角(h,0)；
右上角点②(w,0)被搬到新图像的右下角(h,w)；
右下角③(w, h)被搬到新图像的左下角(0,w)
以此类推，可以发现(x0, y0)和(x1, y1)之间存在以下规律：
x1=y0;y1=−x0+w
对于其他各种几何变换，平移、缩放、镜像等，我们都可以用类似的方法进行运算。因此可以把上式写成通用的形式：

x1=axx0+bxy0+cx

y1=ayx0+byy0+cy

在顺时针旋转90度的例子中，
ax=0,bx=1,cx=0;ay=−1,by=0,cy=w
更一般的，我们可以把上面写成矩阵形式：

(x1y1)=(axaybxbycxcy)×⎛⎝⎜x0y01⎞⎠⎟

或者齐次形式。齐次矩阵的作用后面介绍。

⎛⎝⎜x1y11⎞⎠⎟=⎛⎝⎜axay0bxby0cxcy1⎞⎠⎟×⎛⎝⎜x0y01⎞⎠⎟

我们把矩阵 MT=⎛⎝⎜axay0bxby0cxcy1⎞⎠⎟ 称作放射矩阵。

各种典型变换的仿射矩阵

w为原图像的宽度，h为原图像的高度。
顺时针旋转90度
MT=⎛⎝⎜0−101000w1⎞⎠⎟
旋转180度
MT=⎛⎝⎜−1000−10wh1⎞⎠⎟
逆时针旋转270度
MT=⎛⎝⎜010−100h01⎞⎠⎟
严格讲以上的转置操作是以(0,0)为中心的旋转和平移的合成。因为以(0,0)为中心旋转的结果在负的区域（2，3或者4象限）。不能显示在目标图像中。

平移（x方向平移p, y方向平移q)
MT=⎛⎝⎜100010pq1⎞⎠⎟
水平镜像
MT=⎛⎝⎜−100010w01⎞⎠⎟
缩放s倍
MT=⎛⎝⎜s000s000s⎞⎠⎟

OpenCV中仿射变换的实现

OpenCV中提供了一个函数对图像进行仿射变换。

void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int
flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar&
borderValue=Scalar())

其中src为原始图像，dst为变换后的图像，M就是上面提到的仿射矩阵（2x3，非齐次）。dsize是新图像的大小。其他参数后面介绍。

函数是如何工作的

（1）为dst申请一个内存空间，大小为dsize。(宽度x高度的二维矩阵）
（2）计算仿射矩阵 M 的逆矩阵 M−1
（3）扫描目标图像dst中的每个点 (x1,y1),x1=0...w1,y1=0...h1 . w1,h1 为新图像的宽度和高度。
（4）通过以下式子计算目标图像的点 (x1,y1) 对应源图像点 (x0,y0) .

(x0y0)=M−1×⎛⎝⎜x1y11⎞⎠⎟

（5）填充目标图像 dst(x1,y1)=src(x0,y0)

但是这个计算过程可能遇到一些问题
（1）通过 (x1,y1) 计算得到的 (x0,y0) 可能是小数，而原图像中的像素只存在于与整数。
这时就要通过差值的方法求得两个像素中间点的亮度。差值算法可以在warpAffine()函数的参数flag中指定。
（2）计算得到的 (x0,y0) 可能超出原图像范围。
这时用什么值来填充可以通过参数boarderMode和boarderValue来指定。比如填充一个固定的颜色，或者使用源图像边缘的颜色等。具体参考OpenCv手册。
（3）如果warpAffine()函数被用于视频处理中，每帧画面用的都是相同的仿射矩阵M。每次调用warpAffine()函数都会计算一次M的逆矩阵。可以在flag参数中指定WARP_INVERSE_MAP，并且直接传递 M−1 给函数。可以避免重复计算逆矩阵。

仿射变换优化

仿射变换的合成（级联）

如果需要对图像同时进行旋转，平移，缩放等多重仿射变换。可以把各个变换的仿射矩阵相乘得到总的仿射矩阵，做一次调仿射变换运算即可。仿射矩阵大小为3x3，对仿射矩阵的运算量远少于一次仿射变换运算。
证明：
假设原图像为 src(x0,y0) , 第一次变换（例如旋转）后的图像为 dst1(x1,y1) ，第二次变化（平移）后的图像为 dst2(x2,y2) ，则有
⎛⎝⎜x1y11⎞⎠⎟=M1×⎛⎝⎜x0y01⎞⎠⎟ , ⎛⎝⎜x2y21⎞⎠⎟=M2×⎛⎝⎜x1y11⎞⎠⎟
因此
⎛⎝⎜x2y21⎞⎠⎟=M2×M1×⎛⎝⎜x0y01⎞⎠⎟
MT=M2×M1
其中 M1 为第一次变换（旋转）的仿射矩阵， M2 为第二次变换（平移）的仿射矩阵， MT 为合成的仿射矩阵。所有的仿射矩阵都为3x3，这也是使用齐次矩阵的作用。

计算的优化

可以将 MT 的逆矩阵 M−1 传给warpAffine()，可以节省每次计算逆矩阵的时间。（有待测试）