Cascade R-CNN论文学习

原文链接： https://blog.csdn.net/qq_21949357/article/details/80046867

论文链接：https://arxiv.org/abs/1712.00726
代码链接：https://github.com/zhaoweicai/cascade-rcnn

这篇论文是2018年CVPR的文章，大致读了下是非常有趣且有启发性的工作。这篇文章中，作者对目标检测问题中的两个核心，分类和定位做出了细致的分析和观察，并从这样的观察中得到启发，提出了一个非常简单易行，但是效果十分显著的方法。

这篇文章的基础是双阶段的检测器，如R-CNN和RFCN等，这些双阶段检测器中都会有一个header的结构来对每个候选框同时做两件事情：分类和边框回归。在分类中，每个候选框会根据一个IoU阈值来判断正样本还是负样本。在边框回归中，每个被标记为正样本的边框会根据它所对应的ground truth边框的位置来更新它自己的位置。

本文主要针对的是检测问题中的IoU阈值选取问题。IoU阈值选取越高就越容易得到高质量的样本，但是一味地选取高阈值会引发两个问题：

• 样本减少引发的过拟合问题；
• 在训练和推理时，使用不一样的阈值很容易导致mismatch（下面会有介绍）。

作者为了解决上述问题就提出了一种多阶段的网络结构，核心就是利用不断提高的阈值，在保证样本数不减少的情况下训练出高质量的检测器。

1. Key Ideas

检测问题和分类问题有很大不同，检测问题通过IoU来判断样本是否为正样本，因此IoU的选取对训练和推理的影响都很大，来看作者做的一组实验：

先看左图，横轴是候选框的IoU，纵轴是经过边框回归后得到的新的IoU，不同的线条表示不同阈值训练出来的检测器，显然新的IoU越高，说明检测器进行回归的性能越好。可以看到在[0.55, 0.6]范围内，阈值为0.5的检测器表现最好。在[0.6, 0.75]范围内，阈值为0.6的检测器性能最佳。而到了0.75之后，阈值为0.7的检测器就最好了。

这说明，只有候选框自身的阈值与训练器训练用的阈值较为接近时，训练器的性能才最好。如果两个阈值相距比较远，就是我们前面提到的mismatch的问题了。

从图中我们可以意识到，单一阈值训练出来的检测器效果非常有限，以现在最常见的阈值0.5为例，由于$IoU>0.5$的所有的候选框都会被选中，那么对于$IoU\in [0.6,0.95]$的候选框来说，检测器的表现就差许多了。那么我们能否直接使用0.7这个高阈值呢？毕竟这样子$[0.5,0.7]$的候选框都被排除了，在横轴$[0.7,0.95]$之间，红色线条的表现似乎不差。但是看到右图就会发现，实际上该检测器的性能反而是最低的。原因是这样子训练样本大大减少，过拟合问题非常严重。

如何保证候选框的高质量而又不减少训练样本呢？作者提出了**Cascade R-CNN，用一个阶段检测器的输出去训练下一个阶段的检测器。**留意到左图大部分线条都是在$y=x$的灰色线条之上，说明一个候选框在经过检测器后，它的IoU几乎必然是增加的。那么再经过一个更大阈值训练的检测器，它的IoU会更好。

比如，有三个串联起来的用$0.5,0.6,0.7$阈值训练出来的检测器，有一个IoU为0.55的候选框，经过0.5的候选框后，IoU变为0.75；再经过0.6的检测器后，IoU变为了0.82；再经过0.7的检测器后，最终IoU变为了0.87。比任何一个单独的检测器的结果都要好。除了IoU得到改善的好处，我们也可以有效地避免过拟合问题。因为每经过一个检测器，候选框的IoU都更高，样本质量更好了，那么即使我下一个检测器阈值设置得比较高，也不会有太多的样本被刷掉，这样就可以保证样本数量避免过拟合问题。

2. Related Works

作者还把他的工作和类似的几种工作做了实验比较。在论文中是分开的，这里统一列出来方便大家对比，先看一张图：

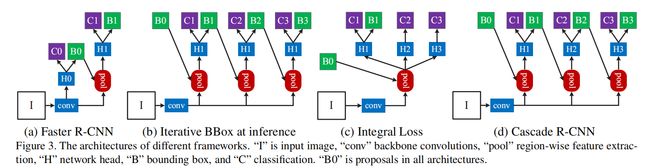
Iterative Bounding Box 及对比

这是目前几个非常典型的工作。图(b)的Iterative Bounding Box为了定位准确，采用了级联结构来对边框进行回归，使用的是完全一样的级联结构。但是这样一来，就有几个问题。

• 单一阈值0.5无法对所有的候选框都得到良好的效果，如第一部分的图所示，候选框经过0.5阈值的检测器之后，其IoU都在0.75以上了，再使用这一阈值并不明智；
• 检测器会改变样本的分布，这时候再使用同一个结构效果也不好，如下图所示：

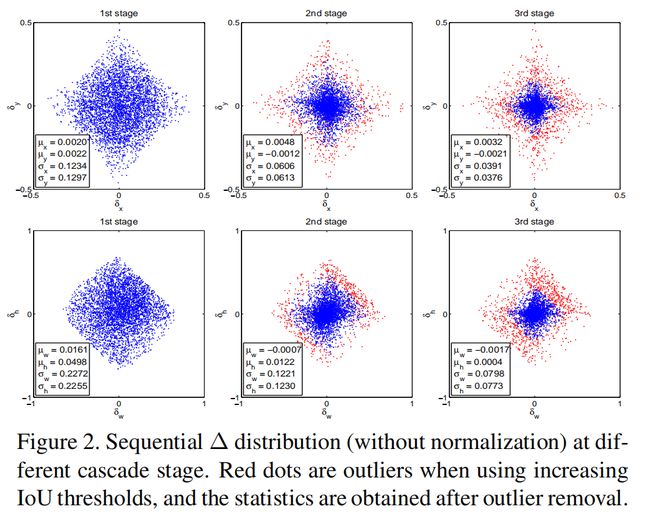
第一行横纵轴分别是回归目标中的边框的$x$和$y$方向的偏移量；第二行横纵轴分别是回归目标中的边框的宽和高的偏移量。我们可以发现，从第一阶段到第二阶段，候选框的分布其实已经发生了很大的变化，因为很多噪声经过边框回归也提高了其IoU，第二阶段和第三阶段中的那些红点已经属于outliers，如果不提高阈值来去除它们，就会引入大量的噪声干扰，对结果不利。从这里可以看出，阈值的选取本质上就是一个重采样的过程，保证了样本的质量。

当然，这里会有另一个问题，我们这样子做会减少样本数量么？虽然第一部分给了比较直观感性的解释，但是似乎还不够。作者给出了更加详细的实验证明：

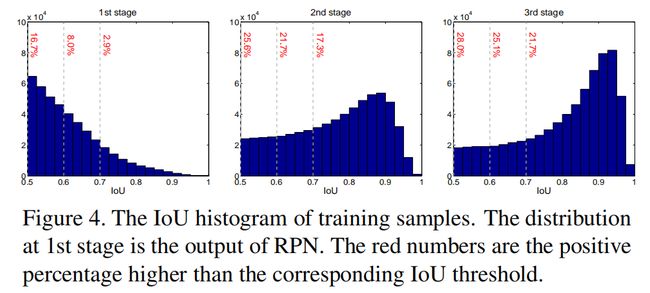
从这张图，我们可以看到，第一阶段中大于0.5的，第二阶段大于0.6的，第三阶段大于0.7的候选框，在这一过程中候选框的样本数量确实没有特别大的改变，甚至还有些许的提升，和上图结合起来看证明非常有说服力了。总结起来就是：

• 级联回归不断改变候选框的分布，并且通过调整阈值的方式重采样；
• 在训练和推理时都会使用级联的方式，并没有偏差问题；
• 级联重采样后的每个检测器，都对重采样后的样本是最优的，没有mismatch问题；

Integral Loss

Integral loss 实际上没有使用级联结构，从上图3©可以看出来，它只是使用了不同的阈值来进行分类，然后融合它们的结果来进行分类推理，并没有同时进行边框回归。作者认为，从图4中第一个图可以看出，当IoU提高的时候，候选框的比重下降的非常迅速，这种方法并没有从根本上解决过拟合的问题。另外，这种结构使用了多个高阈值的分类器，训练阈值却只有一个，必然导致mismatch的问题，影响性能。

3. Experiments and Results

Cascade R-CNN的结构可以参见图3(d)。

最后总结一下，作者最终确定的结构一共是4个阶段：1个RPN+3个检测器（阈值分别为$0.5,0.6,0.7$）。后面三个检测器按照之前的介绍，每个检测器的输入都是上一个检测器进行了边框回归后的结果，实现思路应该类似于Faster R-CNN等双阶段检测器的第二个阶段。

这个提升还是相当惊艳的。特别需要说明的一点是，对于目前流行的检测结构来说，特征提取是耗时最多的，因此尽管Cascade R-CNN增加了比较多的参数，但是速度的影响并没有想象中的大，具体可以参考下表：

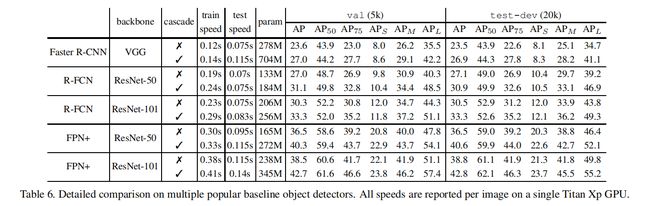
实际上，论文中还有相当多的部分没有提及。这篇文章还做了大量的对比实验，例如通过添加ground truth来提高proposal的质量从而验证mismatch问题；通过添加stages来分析适合的级联阶段数等等；包括一些和第2部分中提到的两种思路的对比等等，可以说是有理有据……再加上不俗的效果和晓畅通俗的语言，还是非常值得阅读的，另外作者的code也已经发布，有兴趣的同学可以前去观摩~

4. Conclusion

引用Naiyan Wang大神的评论吧：Detection其实并不是一个很合适的分类问题，没有一个明确的离散的正负样本的定义，而是通过IoU来连续定义的。但是IoU这个指标很难通过gradient descent来优化，虽然之前也有一些IoU loss的工作，但是效果并不理想。Cascade R-CNN 便是一个在这个方向上很好的尝试。