瀑布流排序中的position偏置消除的实验

前言

瀑布流排序中，用户首先看到的是前面的商品，排在前面的商品有天然的优势，用户的点击率会偏高，

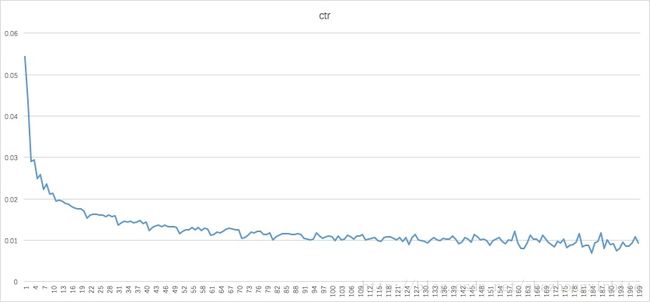
我们观察cpc广告的某个场景的ctr随位置的统计衰减图：



图1: 图中横坐标是排序位置，纵坐标为该位置一天的ctr

大家都有个共识，实际商品表现出来的ctr和商品实际的点击质量是有偏差的，这里的偏差有很大的因素是有展现的位置引起的

如何消除位置偏置

不同的场景要求不一样，实验分两个场景进行

bid* ctr 排序场景

对于同一个位置不同的商品消除的偏置幅度是一样的：

ctr1beforctr1after=ctr2beforctr2after=...=ctrnbeforctrnafter

加权和类似的rank场景

ctr1befor−ctr1after=ctr2befor−ctr2after=...=ctrnbefor−ctrnafter

结论

1. 利用固定position=n来 predict广告的ctr方式部分达到消除position偏置的作用，不过不同的模型和场景必须谨慎选择n值
2. 利用独立position建模，可以起到消除上面n的选择问题
3. 加权平均类似的rank场景，bid *ctr 排序，这两个场景在处理position的时候差别很大

下面我们来看下3个实验的对比

一.普通的线性模型

ctr=σ(w0pi+w∗xi+b)

其中 wo,w 是线性模型的参数， pi,xi 分别是position和其他的特征的样本

假设我们在predict的过程中是使用position=1来消除偏置

那么

ctri=11+e−wxi+b+δ

其中 δ=w0p1 ，然后对于所有predict的样本 b+δ 是常量偏置

对于 f(x)=σ(x)
Δy=f‘(x)Δx
当 f(x)<0.5 时，倒数 是递增的，x越大，单位x变化带来的y变化倍数更大
所以这里的 δ 在ctr的绝对值上面是有放大作用的

看下放大的倍数：

f‘(x)=y(1−y) 

当真实ctr在0附近时，导数值最大，y=0.03 是y=0.02 导数的1.5倍

实验：
采用线上app search一天的数据，实验选取线上十几个点击反馈类型的特征， train/validation 的auc 大概在 0.653左右

横轴：ctr区间，纵轴：商品使用不同的position来predict的个数占比


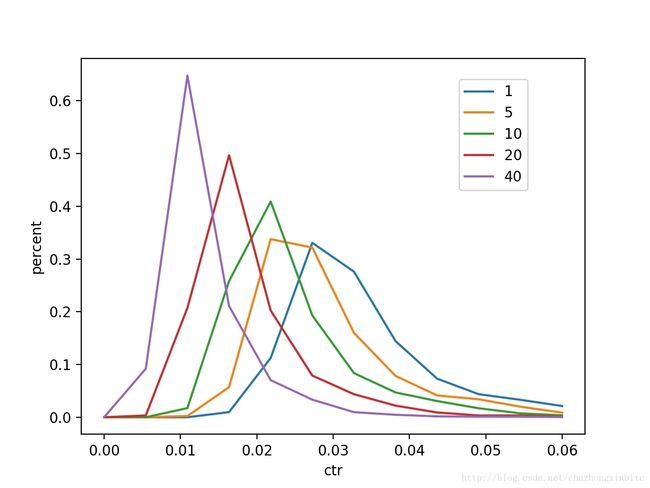
可以很清晰的看到，position越前面，预测的整体ctr越高

我们在两个实际的场景来分析它增加的绝对值和倍数：

1. 线性加权和

score=a∗scoreother+ctr

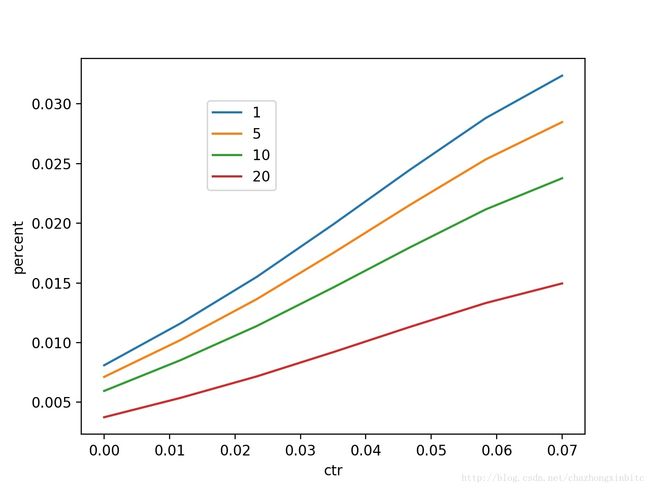
那么整体score对 ctr波动的绝对值比较敏感：

横轴：ctr区间，纵轴：不同position做predict后相对position=40 增加的幅度


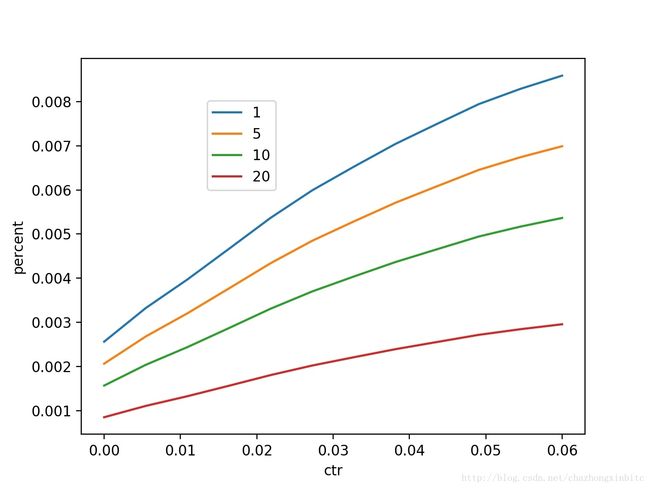
我们可以看到，高ctr 在postion的bais里面有正向的收益

2. bid*ctr

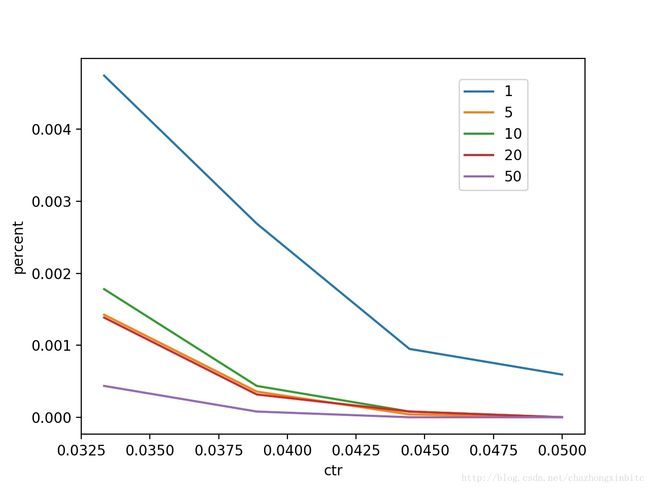
这里考虑的是ctr比例波动的倍数

横轴：ctr区间，纵轴：不同position做predict后相对position=40 增加的倍数


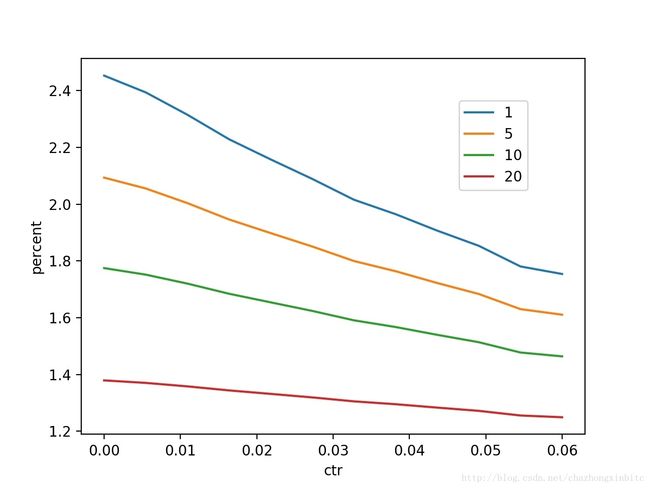
注意, 模型效果：
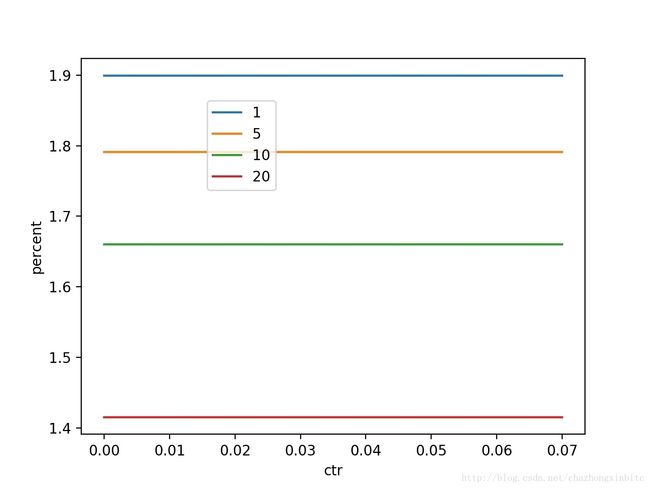
假设我们不对postion的参数进行正则，让模型自己学习合适的参数，

position= 1:

所有参数的线性和：
w0pi+w∗xi+b=−1.66156
w∗xi+b=−3.55709219

position的权重和：
w0pi=1.8955

其中 w0pi 带来的效果过大，以至于和其他所有特征相加可以抗衡

如果稍微对 w0pi 加一个正则，可以看到，波动的幅度明显降低，效果如下图


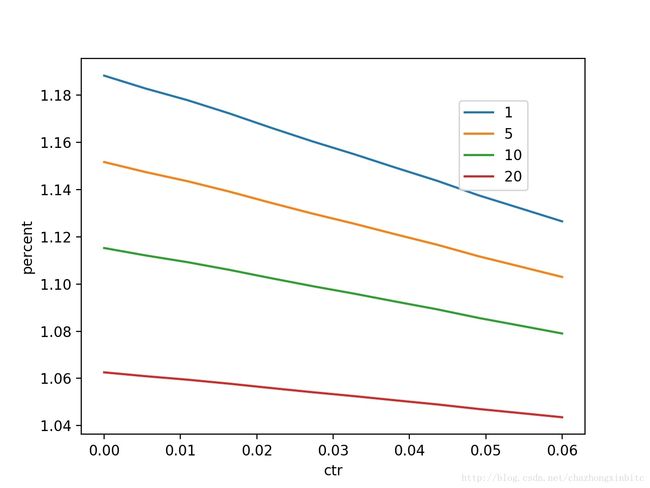
position 的处理在不同的场景，n的选择造成的结果完全是相反的

二. xgboost

线上经验可以知道，position在ctr预估中重要性排第一，但是模型其实不是独立学习position单独的特征，他们是有交叉的作用

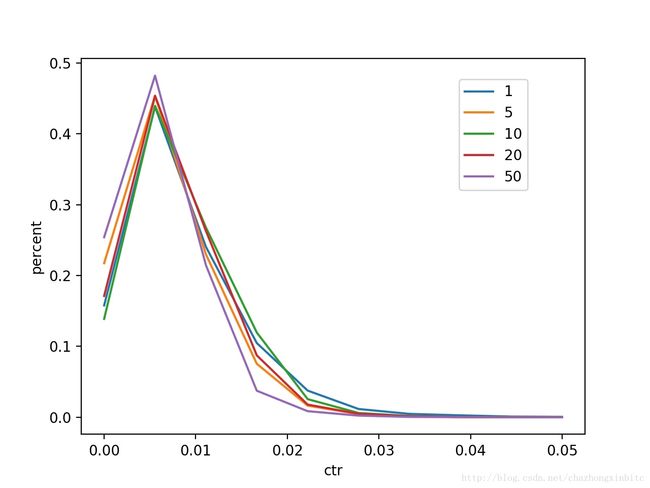
下面看下利用不同position做predict的时候商品ctr下面的分布

大致的情况是：position=1 比 psotion=20，50的商品整体ctr要高

整体图：横轴-ctr, 纵轴-商品占比，不同的曲线代表利用不同的position 出来的占比图


头部ctr的商品图


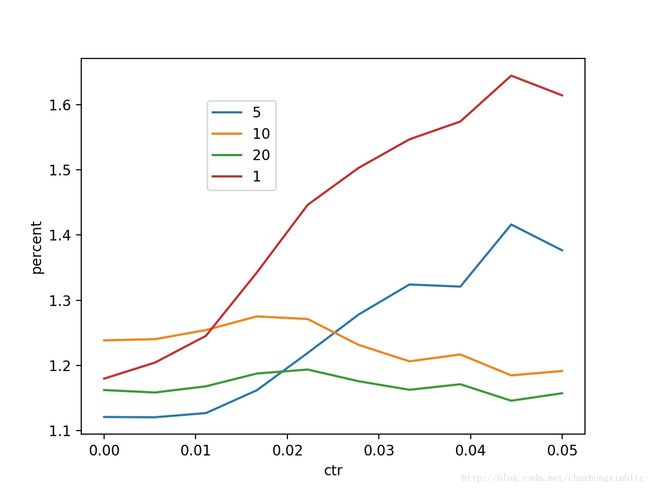
1. 线性加权和

使用position=1来predict 商品的ctr的时候，对ctr绝对值的增加主要是1和其他位置有区别


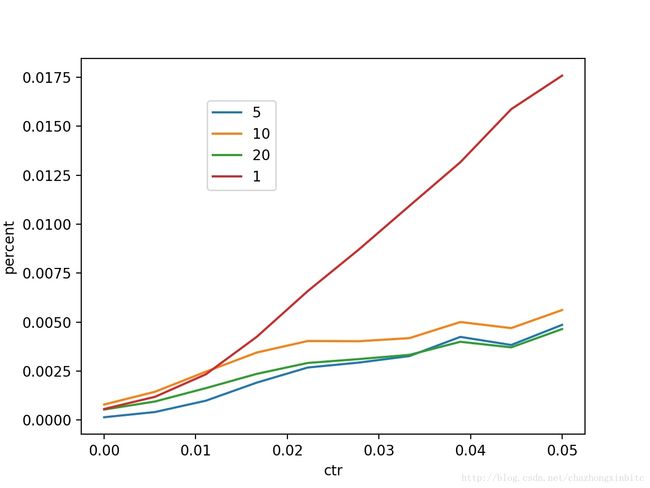
2. bid*ctr

倍数方面，position=1，5 都是在高ctr区间有优势的


xgboost是一致的，就是对ctr高的商品有优势

三. position bais 独立建模

position bais 独立建模也和我们最终需要怎么使用这个ctr score有关，假设我们是bid*ctr 排序，我们更倾向于：
score=score(position)∗ctr
score=sigma(f(pi))∗σ(wxi+b)

假设ctr 还要和其他的分数进行加权和的处理: a*score1 + ctr
我们倾向于
score=score(position)+ctr
score=sigma(f(pi))+σ(wxi+b)

这里我们以第一个来做实验

因为根据上面的ctr随位置的指数衰减的图，我们认为
f(x)=eax+be

这样
score(position)=σ(f(pi))
是一个固定的函数，和具体的样本无关，只是和整体的样本分布有关

实验：
采用线上app search一天的数据，实验选取线上十几个点击反馈类型的特征， train/validation 的auc 大概在 0.653左右, 两个auc是持平的

下面是 score(position) 的分布：
注意，虽然在迭代十几轮之后，auc和loss基本没有变化不大，但是 bais score的参数一直都是在更新的


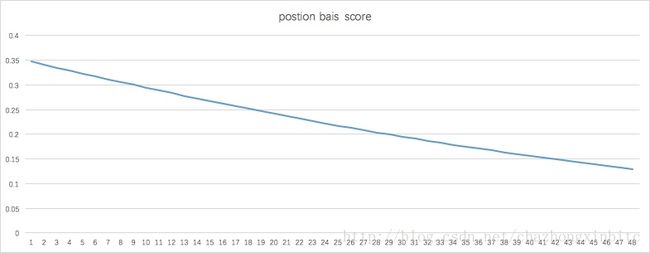
可以看到这里得到的postion bais score 随位置的下拉，衰减的不是很快，图1中很快的指数级别衰减，很各个位置的商品本身质量有关，毕竟排在前面的广告ctr一般不低

1. 线性加权和

下图可以看到，这种建模在这种场景下选择不同的n是有偏置的



2. bid*ctr

这个对于选择n 进行predict来说，是没有偏置的，随便选择哪个都行