VAE(Variational Autoencoder)简单推导及理解

概述

  变分自编码器（Variational auto-encoder，VAE） 是一类重要的生成模型（generative model），它于2013年由Diederik P.Kingma和Max Welling提出¹。2016年Carl Doersch写了一篇VAEs的tutorial²，对VAEs做了更详细的介绍，比文献¹更易懂（墙裂推荐）。
  vae是什么：vae就是通过Encoder对输入（我们这里以图片为输入）进行高效编码，然后由Decoder使用编码还原出图片，在理想情况下，还原输出的图片应该与原图片极相近。
  vae网络结构组成：可以大致分成Encoder和Decoder两部分（如下图）。对于输入图片，Encoder将提取得到编码：一个mean vector和一个deviation vector，然后将这个编码（两个vector）作为Decoder的输入，最终输出一张和原图相近的图片。

VAE公式推算

  定义函数： 由上面可知，vae想要还原输出的图片与原图片尽量相似。对于这个目标，我们也可以换一个角度想：只看decode，其输入是从一个固定分布中抽取的编码，只要decode最后输出的图片与我们训练的数据库中的图片尽量相似就好。那么如何衡量这个相似程度呢，如果还原输出的图片集中出现训练集中的原图的概率越大，那么我们也可以认为输出与原图片越相似了，即：相似度=原图出现的概率。也即通过训练使得下式最大化。
$$\begin{gathered} \max L=\sum _x\log P(x) \\ whileP(x)={\int }_{z}P(z)P(x|z)dz \end{gathered}$$
  上式中假设整个系统产生某张图片$x$的概率是$P(x)$；编码器Encoder使用$q(z|x)$来表示，表示当输入图片$x$时，Encoder输出编码$z$的概率；$P(z)$表示从某一固定分布（常用标准正态分布）中随机采样得到编码z的概率；解码器Decoder使用$P(x|z)$来表示，表示当输入编码$z$时，输出图片$x$的概率。
  公式推导： 对于上述公式，并没有出现编码器Encoder，所以下面通过将$q(z|x)$加入式子中，然后通过推导，以解释训练的过程及损失函数的定义。
$$\{\begin{array}{ll}\log P(x)& ={\int }_{z}q(z|x)\log P(x)dz\\ & \\ & ={\int }_{z}q(z|x)\log (\frac{P(z,x)}{P(z|x)})dz={\int }_{z}q(z|x)\log (\frac{P(z,x)}{q(z|x)}\frac{q(z|x)}{P(z|x)})dz\\ & \\ & =\underset{lowerbound{L}_b}{{\int }_{z}q(z|x)\log (\frac{P(z,x)}{q(z|x)})dz}+\underset{KL(q(z|x)||P(z|x)\ge 0}{{\int }_{z}q(z|x)\log (\frac{q(z|x)}{P(z|x)})dz}\\ & \\ & \ge \underset{lowerbound{L}_b}{{\int }_{z}q(z|x)\log (\frac{P(x|z)P(z)}{q(z|x)})dz}\end{array}$$
  于是得到下面的式子：
$$\{\begin{array}{l}\log P(x)=\{L_b+KL(q(z|x)||P(z|x))\}\le 0\\ \\ KL(q(z|x)||P(z|x))\ge 0\\ \\ L_b={\int }_{z}q(z|x)\log (\frac{P(x|z)P(z)}{q(z|x)})dz\le 0\end{array}$$
  对于$L_b$，可以再次进行分解如下：
$$\{\begin{array}{ll}{L}_b& =\int q(z|x)\log (\frac{P(z,x)}{q(z|x)})dz=\int q(z|x)\log (\frac{P(x|z)P(z)}{q(z|x)})dz\\ & \\ & =\underset{-KL(q(z|x)||P(z))}{\int q(z|x)\log (\frac{P(z)}{q(z|x)})dz}+\int q(z|x)\log P(x|z)dz\end{array}$$

VAE训练过程

训练的最终目标

$$\max L=\sum _x\log P(x)=\sum _x\log {\int }_{z}P(z)P(x|z)dz$$
  其中$x$表示从真实图片数据中随机抽取的图片。实际上，要最大化上式，也就是最大化每张真实图片$x$出现的概率，也就是说对于某一张图片$x$，上式等同于：
$$\max L=\sum _x\log P(x)⟹\underset{eachx}{\max }\log P(x)$$
  下面的过程中，仅仅是以一张图片$x$作为讨论对象，通过训练达到：
$$\max \log P(x)$$

训练步骤，两步走

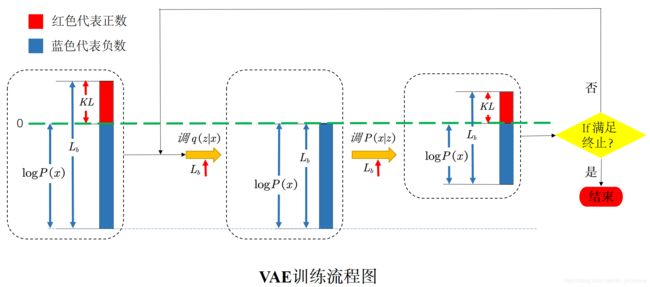
  VAE的训练过程中，我认为实际上就是如同EM 算法，实际也是分为两步，然后两个步骤不断迭代进行（你拍一我拍一），最终使得目标函数不断变大，迭代步骤大致如上面的流程图所示（图中对于$\ge 0$的数使用红色表示，对于$<0$的数使用蓝色表示)。下面便是两个步骤的具体介绍。

1、调整Encoder（ 即$q(z|x)$ ）增大 $L_b$ :

  由上面的推算易知，调整 $q(z|x)$ 不会影响到 $\log P(x)$ 值，但是能改变 $L_b$，又因为$\log P(x)=L_b+KL(q(z|x)||P(z|x))$， 所以可以调整 $q(z|x)$ 使得 $L_b$ 不断增大，在理想情况下，最终使得：$L_b=\log P(x)$，$KL=0$，如上图流程图中的第一个黄色箭头所示（注意：因为$L_b\le 0$，所以$L_b\uparrow$ 时其在图中的长度会变短）。
  至于如何调整 $q(z|x)$ 使得 $L_b\uparrow$ ，我们不妨看公式 $L_b=\underset{-KL(q(z|x)||P(z))}{\int q(z|x)\log (\frac{P(z)}{q(z|x)})dz}+\int q(z|x)\log P(x|z)dz$，公式中右边一共有两项，那么我们如果能调整 $q(z|x)$ 使得两项都增大，那便能达到目标。但是可能因为第二项不好量化训练（我是这样理解的），所以在VAE的训练中，都只是使得第一项（即$-KL(q(z|x)||P(z))$）不断增大，也即是不断减小$KL(q(z|x)||P(z))$，实际也是让$q(z|x)$接近于$P(z)$（一般将$P(z)$设置为标准正态分布）。

  上图（图来自李宏毅老师的课件）说明了如何设置损失函数进行训练，以使得$q(z|x)$接近于$P(z)$（其中$P(z)$设置为标准正态分布）。其中损失函数为（原因可参考这里）：
$$\min los{s}_1=\sum _{i=1}^3(exp({\sigma }_i)-(1+{\sigma }_i)+(m_i{)}^2)$$
  显然可以推算，当损失函数达到最小值的时候，会有${\sigma }_i=0，m_i=0$，实际上这个时候也就会有$z_i=exp({\sigma }_i)\times e_i+m_i$服从标准的正态分布，因此有$q(z|x)=P(z)$。

2、调整Decoder（ 即$P(x|z)$ ）增大 $L_b$ ：

  由推导可知，调整 $P(x|z)$ 不仅能改变 $\log P(x)$，也能改变$L_b$。在理想情况下，经过上面一步后，会出现$KL=0$，这时我们再调整$P(x|z)$使得$L_b$增大，同时一定会有$KL\ge 0$也随之变大，这样便会$\log P(x)\uparrow =L_b\uparrow +KL(q(z|x)||P(z|x))\uparrow$，于是$\log P(x)$也在变大，如前面流程图中的第二个黄色箭头所示（注意：因为$L_b\le 0$，所以$L_b\uparrow$ 时其在图中的长度会变短）。
  至于如何调整 $P(x|z)$ 使得 $L_b\uparrow$ ，我们不妨看公式 $L_b=\underset{-KL(q(z|x)||P(z))}{\int q(z|x)\log (\frac{P(z)}{q(z|x)})dz}+\int q(z|x)\log P(x|z)dz$。显然，调整 $P(x|z)$ 对右边第一项是没有影响的，只会影响到第二项 $\int q(z|x)\log P(x|z)dz$，由蒙特卡罗方法可以得到损失函数为：
$$\max los{s}_2=\int q(z|x)\log P(x|z)dz=E_{q(z|x)}[\log P(x|z)]\simeq \frac{1}{L}\sum _{l=1}^L\log P(x^{(i)}|z^{(i,l)})$$
  其中$x^{(i)}$是从真实数据中采样得到的第$i$个数据；以$x^{(i)}$作为Encoder的输入，随后从编码器$q(z|x^{(i)})$中抽取$L$个数据$z^{(i,l)}$。实际上就是调整Decoder（ 即$P(x|z)$ ），使得以$x^{(i)}$作为Encoder的输入，编码采样得到多个$z^{(i,l)}$，最后能用Decoder最大概率地从$z^{(i,l)}$中恢复出$x^{(i)}$。

实际训练的损失函数

  在实际训练中，通常不是将上面两步分开迭代进行，而是将两步结合起来同时训练，所以最终的损失函数为:
$$\{\begin{array}{ll}\max loss& =-los{s}_1+los{s}_2=-KL(q(z|x)||P(z))+\int q(z|x)\log P(x|z)dz\\ & \\ & \simeq {\sum }_{i=1}^3(exp({\sigma }_i)-(1+{\sigma }_i)+(m_i{)}^2)+\frac{1}{L}{\sum }_{l=1}^L\log P(x^{(i)}|z^{(i,l)})\end{array}$$

训练结果

  

  上图² 显示了使用MNIST数据集进行训练，最后从训练好的VAE中采样得到的图片。

---

1. Kingma D P, Welling M. Auto-encoding variational bayes[J]. arXiv preprint arXiv:1312.6114, 2013. ↩︎ ↩︎

2. Doersch C. Tutorial on variational autoencoders[J]. arXiv preprint arXiv:1606.05908, 2016. ↩︎ ↩︎