算法 | 盖尔-沙普利(Gale-Shapley)婚姻稳定匹配算法
盖尔-沙普利[Gale-Shapley]婚姻稳定匹配算法
- 1 背景说明
- 2 原理及思路
- 2.1 问题的描述
- 2.2 盖尔-沙普利算法的思路
- 3 程序实现
- 4 结果分析
- 5 后记
概要: 本文将要介绍的盖尔-沙普利稳定匹配算法是一个有趣的算法,可以用来解决某些方面的问题或至少也能提供一些思路:比如男女双方互相挑选对象,或用人单位和毕业生互相选择,或者是在学生选课时等等。本文将仔细说明该算法的原理,并用MATLAB编程演示如何实现这一算法,最后得出若干结论。
关键字: MATLAB;稳定匹配算法
1 背景说明
盖尔-沙普利(Gale-Shapley)稳定匹配算法是美国数学家 David Gale 和 Lloyd Shapley在1962年提出的一种寻找稳定婚姻的策略。这种匹配方式的特点在于:不管需要匹配的总人数有多少、不管他们各自的偏好如何,只要男女人数相等,并且男女双方每个人都能在心中给对方打分,那么应用这种策略后总能得到一个稳定的婚姻搭配。换句话说,他们证明了稳定的婚姻搭配总是存在的。并且这种策略反映了现实生活中的很多真实情况,也不仅仅局限于婚姻匹配。
2 原理及思路
2.1 问题的描述
现在,让我们来更加仔细地描述这个问题。
有N男N女需要寻找结婚对象,并假设他们的性取向全部正常——即婚姻的搭配方式只有男&女这一种。要求是帮助这N男N女中的每个人都成功匹配一个婚姻的对象,并且这个对象必须是稳定的。
什么是稳定呢?举个例子说明:
假设有两对夫妻M1&F2、M2&F1。M1心中更喜欢F1,但是他和F2结婚了,M2心目中更喜欢F2,但是他和F1结婚了,显然这样的婚姻是不稳定的,因为随时都可能发生M1和F1私奔或者M2和F2私奔的情况(当然,在这里我们需要假设情感因素是婚姻绝对的主导,虽然这在生活中基本不存在,但是在数学世界中我们不妨就这么假设)。所以在男女双方做匹配时(也就是结婚的时候)需要做出稳定的选择,以防这种情况的发生。
(PS:博主还很年轻,为了方面我的描述,我下面还是把所有“结婚”描述为“恋爱”好了,勿怪,勿怪~。)
2.2 盖尔-沙普利算法的思路
盖尔-沙普利(Gale-Shapley)稳定匹配算法解决了这一问题,它的思路如下。
首先,男生需要按照希望与之交往的顺序给所有女生排序,即最理想的女友排在最前、最不理想的放在最后。同样,每个女生也需要给男生排序。接着,男生将按照自己的名单一轮一轮地去追求喜欢的女生,女生也将按照自己的名单接受或拒绝对方的追求。
第一轮,每个男生都向自己名单上排在首位的女生表白。此时,一个女生可能面对的情况有三种:没有人跟她表白、只有一人跟她表白、有不止一人跟她表白。在第一种情况下,这个女生什么都不做,继续等待即可;在第二种情况下,女生接受那个人的表白,答应暂时和他做男女朋友;在第三种情况下,女生从所有追求者中选择自己最喜欢的那一位,答应和他暂时做男女朋友,并拒绝其他所有的追求者。
第一轮结束后,有些男生已经有女朋友了而有些男生仍然是单身狗。在第二轮表白行动中,每个单身男都会从所有还没拒绝过自己的女生中选出自己最喜欢的那一个,并向她表白,不管她现在是否是单身。和第一轮一样,每个被表白的女生需要从表白者中选择最喜欢的男生,并拒绝其他追求者。注意,如果这个女生当前已经有男朋友了,当她遇到了更好的追求者时,她将毫不犹豫地和现男友分手,投向新追求者的怀抱。这样以来,一些单身狗将脱单,而一些倒霉的恩爱狗(男)也会被分手,重新进入单身狗的行列。
在以后的每一轮中,单身狗们将发扬愈挫愈勇的顽强精神,继续追求列表中的下一个女生;女生则从包括现男友在内的所有追求者中选择最好的一个,并给其他所有追求者发好人卡。这样一轮一轮地进行下去,直到某个时刻所有人都不再单身,那么下一轮将不会有任何新的表白,每个人的对象也都将固定下来,整个过程自动结束——此时的搭配就一定是稳定的了。
3 程序实现
在弄明白了原理后,写代码其实是最简单的一步。我是用MATLAB写的,不过对于这样一个简单的算法来说用MATLAB写还是用C或者一些其他什么语言写基本没多少差距,可能唯一的不同就是自己的熟练度了。
我的核心代码是一个while循环,内部分为2个部分:男生追求(M:courtship)和女生回复(F:response)。其中男生追求的代码是长这个样子的:
% M: courtship
for i=1:Num % 对于每个男生
if M_sg(i)==1 % 如果他当前是单身
for j=1:Num % 就按喜欢程度从高到低给每位女生排序(不管女生是否单身)
if M(i,j)~=0 % 选择没有拒绝过自己的女生中最喜欢的那一个
for k=1: Num % 发出情书
if F(M(i,j),k)==i
F_mark(M(i,j),k)=1;
break;
end
end
break;
end
end
end
end
而女生回复的代码是长这个样子的:
% F: response
for i=1:Num
if sum(F_mark(i,:)~=0) % 每个收到情书的女生(不论是否单身)
for j=1:Num
if F_mark(i,j)==1 % 只接受其中最喜欢的男生的情书
F_cp(i)=F(i,j); % 于是这个女生有了CP
M_cp(F(i,j))=i; % 对应的男生也有了CP
M_sg(F(i,j))=0; % 同时,那个男生摘掉了单身狗的帽子
if j上面这两段代码是这个算法的核心内容,看上去是不是so easy?读者如果想试一试,只要把它们连在一起套在一个while里就好了,当然别忘了定义一些代码里出现过的变量之类的准备工作。这里比较绕人的是于二维数组的应用,需要仔细对照数组的下标,什么i、j、k、s可千万别弄错了。至于其他的部分,我也利用了MATLAB的便利绘制了一些图片作比较和分析,下面我会讲到的。
4 结果分析
在付出了一个下午的辛勤劳动后,代码终于写出来并调通了。下面将简单介绍程序运行的结果并作简要分析。
首先展示的是100对男生女生的匹配结果,如图1所示:
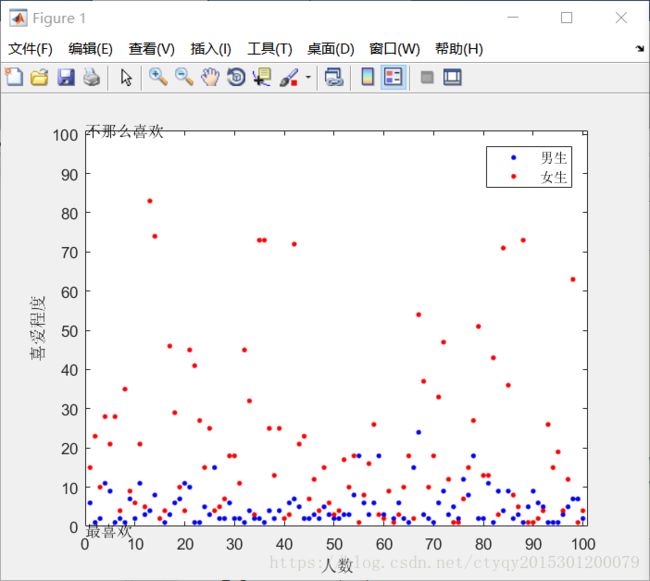
图中蓝色小点的纵坐标表示男生最终追到的女生在自己列表上的排名,排名数字越小,表示该男生对现女友越喜爱,即当前的女友越接近自己的最爱。红点代表女生,所代表的意义和蓝点是一样的,即红色小点的纵坐标表示女生最终接受的男友在自己列表上的排名。横坐标的人数实际上是“男女生对数”,因此每个横坐标上有2个数据点,红、蓝各一。
再仔细地看这张图我们会发现在发多数情况下蓝色小点处于其相对应的红色小点的下方。很明显:男生找到的伴侣离自己的最爱比女生更近——而且还不止一点点!也就是说,在这种策略下,男生更容易收获自己的女神而女神则非常难获得自己的男神。
为了更清晰地表现这一结论,我制作了下方的图2。其中横坐标表示男女匹配的轮数,纵坐标表示在该轮匹配结束后,100名男生女生的对象在自己列表中排名的平均值(注:当前为单身的男生女生不计)。
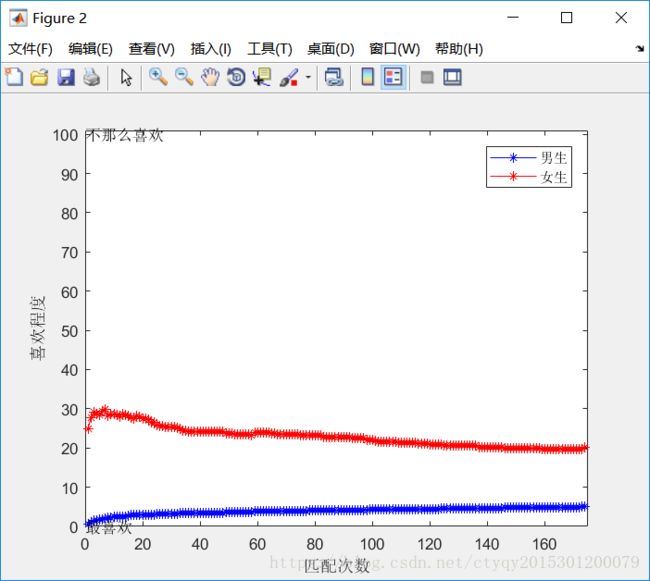
图中蓝色表示男生,红色表示女生,横坐标为匹配轮数,纵坐标为该轮数完成后对当前对象的平均喜爱程度:纵坐标为排名,数值越小喜爱程度越高。
从图中明显可以看出:男生对自己的女友的平均喜爱程度大大高于女生对自己男友的平均喜爱程度。随着匹配轮数的增加,男生对女友的喜爱程度逐渐下降至平稳,女生对自己男友喜爱程度逐渐上升至平稳;而且在第一轮时非单身的男生总的找到自己的“女神”,即最喜爱的女生作为女友。这是由于每次总是男生主动追求,所以在第一轮时,对所有男生来说,只要能匹配到女友,那么该女友就一定是自己的最爱。当然了,在后续的匹配轮中男生也很可能失去自己的女神——除非女神最爱的男生恰好也是自己——然而这种概率并不大。而在后续匹配中,由于仍然是男生主动追求,女生只能在追求自己的人中挑选,所以女生对男友的满意程度总是比不上男生对女友的满意程度——毕竟每个男生都有机会追求自己的女神,而对很多女生来说,直到匹配结束也等不到自己男神的表白。
为了使模拟更加贴近现实,我们不妨设置有1000对男女参与匹配。结果如图3和图4所示。
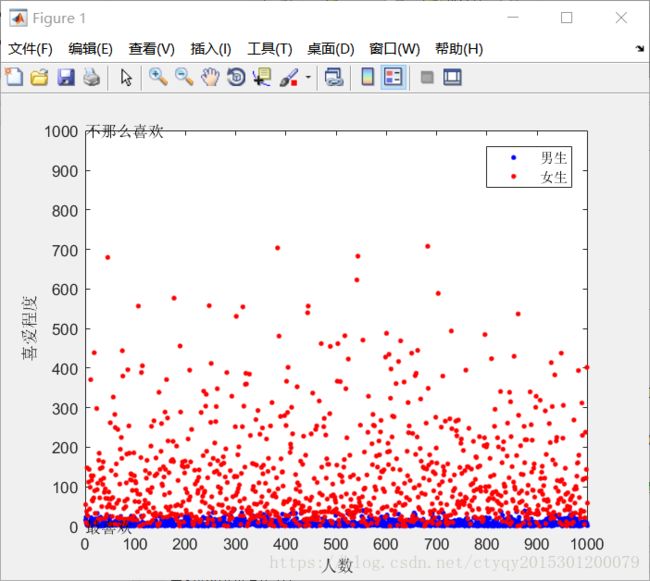
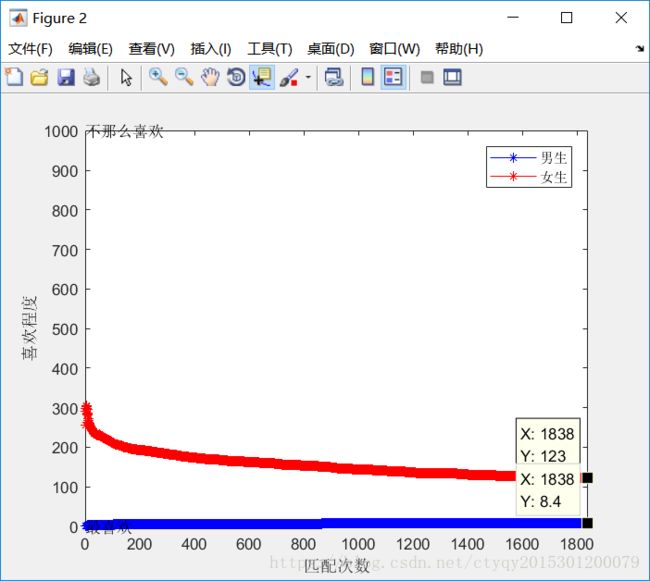
这次一共为1000对男女匹配了1838轮,最终得到了稳定的匹配结果。结果更加直观了,图3蓝色几乎排成一条直线,并且大部分都处在[0,20]区间内,而代表女生的红点则分布得很分散,虽然总地来说呈现“下密上疏”的状态但是远远无法和男生相比。
同样地,喜爱程度随轮数而变化的规律也更加明显。在得到稳定匹配后,男生对女友的平均喜爱程度得分为8.4,而女生的得分为123。因此我们不妨这么认为,在得到稳定匹配后,男生最终获得的女友是男生的喜爱列表上的第8或第9位女生,而女生最终获得的男友则是女生的喜爱列表上的第123位男生(男生女生的喜爱列表上各自有1000名异性的名字),这样看来说是天壤之别也不为过了。
同样的策略也可以用来分析其他类似的互选过程,比如校园招聘。在校招时,经过对所有提交简历的学生的考察和排序,招聘方给列表上的前若干名学生发出邀请;而每个学生也都会得到一份或多份邀请(请自行忽略没有收到邀请的学生和没有收到简历的招聘方,或假设这种情况不存在),学生选择最好的一个并拒绝其他的offer,招聘方在得到第一轮反馈后划掉拒绝自己的学生,并从wait list 中增补所缺名额。这样一轮轮地互选直到双方都满意,那么也就达成了最稳定匹配。在这种情况下,招聘方扮演了男生的角色,而学生则扮演了女生的角色。因此我们可以看到,每年校招时,招聘公司总能招到尽可能优秀的学生,而学生却往往比较难获得最心仪的offer。
还有个比较相似的例子就是高考填志愿。填志愿是考生和学校的互选,不妨就把考生的志愿表看作是上文中男生的“女友列表”,学校在收到考生的“表白”后,会给最好的那一部分发录取通知,相当于上文中的女孩接受了男生的“表白”。而对于没有被录取的学生,系统会将他志愿表上稍次一点的选项发送给对应的学校(男生被当前女生拒绝,向下一位女生表白),而稍次一点的学校也会进行同样的选择。这样反复匹配直至完成。而当学生给志愿表上所有学校都发了入学申请却都遭遇拒绝时,这名学生就会被“退档”,如本一直接转为本二。这在现实生活中是存在的,每个高校的每个专业都会设置一定的退档率,如1:1.05等,设置这样一个规则的原因是学校希望能找到尽可能优秀的学生,也是为了在某种程度上弥补学校因作为上文中的“女生”一方而天然受到的限制。
5 后记
最后需要说明的是,现实生活中的匹配当然不会如本文所描述得那样一丝不苟,但即使如此,这种策略所反映的结果却和生活经验高度吻合。如果说还能有什么启示,那就是:
爱要大胆一点。不论是男生还是女生,主动追求永远比被动等待更有希望获得幸福。
转载时务必注明来源及作者。尊重知识产权从我做起。
代码已上传至网络,欢迎下载,密码是spn2。