手撕代码之其他类型
文章目录
- 一、根据rand7生成rand10(leetcode 470)
- 二、快速幂(leetcode 50)
- 三、数字二进制表示后1的个数(leetcode 191)
- 四、判断点是否在三角形内
- 五、下一个全排列(leetcode 31)
- 六、带精度的开根号(leetcode 69)
- 七、实现strcpy和memcpy
- 八、路径简化(leetcode 71)
- 九、字母异位词分组(leetcode 49)
- 十、lisp语句解析(leetcode 736)
一、根据rand7生成rand10(leetcode 470)
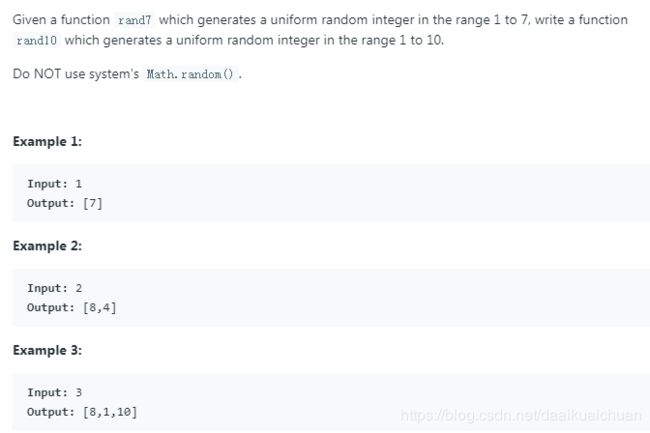
思路:先根据rand7等概率生成rand49【(rand7() - 1) * 7 + (rand7() - 1)】,再生出rand40,最后生成rand10。
class Solution {
public:
// 先生成rand49
int rand49() {
return (rand7() - 1) * 7 + (rand7() - 1);
}
// 再生出rand40
int rand40() {
int r = rand49();
while (r >= 40) {
r = rand49();
}
return r;
}
// 最后生成rand10
int rand10() {
return rand40() % 10 + 1;
}
};
二、快速幂(leetcode 50)

思路:使用递归分治算法,分为偶数、奇数和负数的情况,每次把n缩小一半,这样n最终会缩小到0,任何数的0次方都为1,这时候我们再往回乘。

class Solution {
public:
double myPow(double x, int n) {
if (n == 0)
return 1;
double half = myPow(x, n / 2);
// n为正数或者负数,且为偶数
if (n % 2 == 0)
return half * half;
// n为正数,且为奇数
if (n > 0)
return half * half * x;
// n为负数,且为奇数
return half * half / x;
}
};
三、数字二进制表示后1的个数(leetcode 191)
class Solution {
public:
int hammingWeight(uint32_t n) {
int res = 0;
while (n > 0) {
// 除2取余,看余数有多少个1
if (n % 2 == 1)
res++;
n /= 2;
}
return res;
}
};
四、判断点是否在三角形内
思路:若点P在三角形ABC内,则三角形ABP+三角形ACP+三角形BCP的面积等于三角形ABC。已知三角形三点坐标ABC,如何求三角形面积呢?根据叉乘公式,向量A=(x1,y1) ,向量B=(x2,y2),A x B = x1y2 - x2y1。此时求得的是向量A和向量B的形成的平行四边形的面积,除以2就是三角形的面积了。
#include 五、下一个全排列(leetcode 31)

思路:找到第一个递减的数nums[i],然后找到第一个大于nums[i]的数nums[j],并将两个数交换,最后翻转nums[i]后面的部分。

class Solution {
public:
void nextPermutation(vector<int>& nums) {
int n = nums.size(), i = n - 2, j = n - 1;
// 找到第一个递减的数nums[i]
while (i >= 0 && nums[i] >= nums[i+1])
--i;
// 然后找到第一个大于nums[i]的数nums[j],并将两个数交换
if (i >= 0) {
while (nums[j] <= nums[i])
--j;
swap(nums[i], nums[j]);
}
// 最后翻转nums[i]后面的部分
reverse(nums.begin() + i + 1, nums.end());
}
};
六、带精度的开根号(leetcode 69)
// detal表示精度
double my_sq(double num, double detal)
{
double low = 0, high = num;
double mid = (low + high) / 2;
while (abs(mid * mid - num) > detal)
{
if (mid * mid > num)
high = mid;
else if (mid * mid < num)
low = mid;
mid = (low + high) / 2;
}
return mid;
}
七、实现strcpy和memcpy
char *MyStrcpy(char *pdes, const char *psrc) {
if (pdes == NULL || psrc == NULL)
return NULL;
char *res = pdes;
int len = strlen(psrc), i = len;
if (pdes >= psrc) {
while (i >= 0) {
*(pdes + i) = *(psrc + i);
--i;
}
}
else {
while (*psrc != '\0') {
*pdes = *psrc;
++pdes;
++psrc;
}
*pdes = '\0';
}
return res;
}
void *MyMemcpy(void *dst, const void *src, size_t size) {
char *psrc, *pdst;
if (NULL == dst || NULL == src) {
return NULL;
}
// 自后向前拷贝
if ((src < dst) && (char *)src + size > (char *)dst) {
psrc = (char *)src + size - 1;
pdst = (char *)dst + size - 1;
while (size--) {
*pdst-- = *psrc--;
}
}
else{
psrc = (char *)src;
pdst = (char *)dst;
while (size--) {
*pdst++ = *psrc++;
}
}
return dst;
}
char buf[100] = "abcdefghijk";
MyMemcpy(buf + 2, buf, 5);
printf("%s\n", buf + 2);
char pdes[5], psrc[5] = "1234";
MyStrcpy(psrc + 1, psrc);
cout << psrc << endl;
八、路径简化(leetcode 71)
class Solution {
public:
string simplifyPath(string path) {
vector<string> v;
int i = 0;
while (i < path.size()) {
while (path[i] == '/' && i < path.size()) ++i;
if (i == path.size()) break;
int start = i;
while (path[i] != '/' && i < path.size()) ++i;
int end = i - 1;
string s = path.substr(start, end - start + 1);
if (s == "..") {
if (!v.empty()) v.pop_back();
} else if (s != ".") {
v.push_back(s);
}
}
if (v.empty()) return "/";
string res;
for (int i = 0; i < v.size(); ++i) {
res += '/' + v[i];
}
return res;
}
};
九、字母异位词分组(leetcode 49)

思路:用临时变量保存每一个字符串,对拷贝的字符串排序(如果字符串互为错位词则排序后都是相同的),最后将其存放到map中。
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
vector<vector<string>> res;
map<string, vector<string>> mp;
for (auto str : strs){
string str_tmp = str;
sort(str_tmp.begin(), str_tmp.end());
mp[str_tmp].push_back(str);
}
for (auto m : mp){
res.push_back(m.second);
}
return res;
}
};
十、lisp语句解析(leetcode 736)

对于这种长度不定且每个可能包含子表达式的题,递归是一个很好的选择,由于需要给变量赋值,所以需要建立一个变量和其值之间的映射.
class Solution {
public:
int evaluate(string expression) {
unordered_map<string, int> m;
return helper(expression, m);
}
int helper(string str, unordered_map<string, int> m) {
// 先处理首尾括号
if (str[0] == '-' || (str[0] >= '0' && str[0] <= '9')) return stoi(str);
else if (str[0] != '(') return m[str];
string s = str.substr(1, str.size() - 2);
int cur = 0;
string cmd = parse(s, cur);
if (cmd == "let") {
while (true) {
string var = parse(s, cur);
if (cur > s.size()) return helper(var, m);
string t = parse(s, cur);
m[var] = helper(t, m);
}
} else if (cmd == "add") {
return helper(parse(s, cur), m) + helper(parse(s, cur), m);
} else if (cmd == "mult") {
return helper(parse(s, cur), m) * helper(parse(s, cur), m);
}
}
// 解析
string parse(string& s, int& cur) {
int end = cur + 1, t = cur, cnt = 1;
if (s[cur] == '(') {
while (cnt != 0) {
if (s[end] == '(') ++cnt;
else if (s[end] == ')') --cnt;
++end;
}
} else {
while (end < s.size() && s[end] != ' ') ++end;
}
cur = end + 1;
return s.substr(t, end - t);
}
};


