Classification: Precision/Recall ,ROC, AUC等分类模型评估方法,Multilabel and Multioutput Classification
Classification
-
一.数据集获取及预处理
-
1 数据集导入
-
2数据集划分
-
-
二、binary classification 二元分类器
- 自己实现交叉验证函数
- confusion matrix
- precision/recall tradeoff
- Precision/Recall曲线
- ROC 曲线
- AUC
-
三、Multiclass Classification
- Error Analysis
- numpy broadcast
-
四、 Multilabel Classification 多标签分类
-
五、Multioutput Classification
最常见的监督学习问题是分类和回归问题,此章我们利用mnist数据集完成分类问题的探讨
一.数据集获取及预处理
1. 数据集导入
注意: 数据集导入需要连外网,我将数据集保存在这里
# 引入数据集
from sklearn.datasets import fetch_mldata
import os
import pickle
# 若文件中没存在mnist数据集,则将数据集从网站导入后存入到文件中,
# 若存在直接从文件中获取
if not os.path.exists('mnist.pickle'):
mnist = fetch_mldata('MNIST original')
with open('mnist.pickle', 'wb') as wf:
pickle.dump(mnist, wf)
else:
with open('mnist.pickle', 'rb') as rf:
mnist = pickle.load(rf)
mnist
out:
{‘DESCR’: ‘mldata.org dataset: mnist-original’,
‘COL_NAMES’: [‘label’, ‘data’],
‘target’: array([0., 0., 0., …, 9., 9., 9.]),
‘data’: array([[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0],
…,
[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0]], dtype=uint8)}
X,y = mnist['data'], mnist['target']
print(X.shape)
print(y.shape)
out:
(70000, 784)
(70000,)
显示一张图片 每张图片为 28×2828×28 的灰度图,利用matplotlib imshow()函数随机画一张图
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import matplotlib
number = np.random.choice(len(X))
some_digits = X[number]
some_digits_image = some_digits.reshape(28, 28)
plt.imshow(some_digits_image, cmap=matplotlib.cm.binary, interpolation='nearest')
plt.axis('off')
y[number]
out:
2.数据集划分
将数据集分为测试集和训练集, 并将训练集中的数据顺序打乱(shuffle the training set).这将保证所有的交叉验证子集相似,不至于某些子集缺少了某些数字。
注意:某些学习算法对训练数据个体的顺序十分敏感,如果连续输入很多相似的数据,算法的表现性能很糟糕;但是对于某些时间序列数据而言比如股票票价和天气状况等,打乱顺序并非好事
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
# print(np.unique(y_train))
shuffle_index = np.random.permutation(60000)
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]
二、binary classification 二元分类器
1.创建分类器
简单点,先训练一个二元分类器(Binary classifier),比如判断一个数字是否为5.
np.unique解释 https://docs.scipy.org/doc/numpy/reference/generated/numpy.unique.html
# 重新更改标签
y_train_5 = (y_train == 5.0 )
y_test_5 = (y_test == 5.0 )
# 检查标签的种类
np.unique(y_train_5)
# print(y_test)
# y_test_5
out:
array([False, True])
选择基于随机梯度下降( SGD, stochastic gradient descent)的分类器,该梯度下降算法一次只使用一个样本训练算法,更容易处理大量训练数据,所以SGD也适合于在线学习(online learning).创建一个SGDClassifier
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
out: 训练的SGDClassifier
SGDClassifier(alpha=0.0001, average=False, class_weight=None, epsilon=0.1,
eta0=0.0, fit_intercept=True, l1_ratio=0.15,
learning_rate=‘optimal’, loss=‘hinge’, max_iter=None, n_iter=None,
n_jobs=1, penalty=‘l2’, power_t=0.5, random_state=42, shuffle=True,
tol=None, verbose=0, warm_start=False)
预测图像 上文中some_digits
sgd_clf.predict([some_digits])
out:
array([False])
2. 模型评价
评估一个分类器通常要比评估回归模型更困难,更具有技巧性,所以本章大多数讨论的主题都是评估问题
使用交叉验证测量准确率
关于交叉验证详解 https://blog.csdn.net/dss_dssssd/article/details/82860175
自己实现交叉验证函数:
- StratifiedKFold完成分层抽样,即将数据分成k个folds.然后StratifiedKFold.split返回k个元组的生成器,每个元组的第一个值为训练索引,第二个值为验证索引值
- clone(estimator) : Constructs a new estimator with the same parameters. 使用与estimator相同的参数新创建一个新的estimator
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
# 分为3个folds
skfolds = StratifiedKFold(n_splits=3, random_state=42)
# print(list(skfolds.split(X_train, y_train_5)))
for train_index, test_index in skfolds.split(X_train, y_train_5):
# print(train_index.shape,test_index)
#先创建一个新的estimator
clone_clf = clone(sgd_clf)
X_train_folds = X_train[train_index]
y_train_folds = (y_train_5[train_index])
X_test_fold = X_train[test_index]
y_test_fold = (y_train_5[test_index])
clone_clf.fit(X_train_folds, y_train_folds)
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold)
print(n_correct / len(y_pred))
out:
0.92935
0.96545
0.9593
使用sklearn提供的cross_val_score函数
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring='accuracy')
out:
array([0.92935, 0.96545, 0.9593 ])
confusion matrix
将类A分类为B的次数,比如你想查看将5识别为3的次数,你可以查看矩阵的第5行第3列。
在计算混淆矩阵(confusion matrix)之前,先需要预测值,以便于与真实值比较,当然可以在测试集(test set)上预测,但是现在先不在测试集上预测(切记,只有在项目的最后再能使用测试集),可以使用cross_val_predict()在训练集上预测代替。
和cross_val_score()函数相似,cross_val_predict()也在k个子集上做交叉验证,但返回的不是评估分数,而是在每个测试集上的预测值。简单的就是,每次在k-1个子集上训练,而在余下的1个子集上预测。
以下就是利用cross_val_predict()和confusion_matrix()函数获得混淆矩阵的例子
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
out:
array([[52660, 1919],
[ 999, 4422]], dtype=int64)
在混淆矩阵中,每一行为真实的类别(actual class),每一列为预测的类别(predict class),比如第一行的类别为不是5(被称为 the negative class)的图片,有52660被正确的分类(true negativse),而有1919的图片被分为5(false positives),第二行的类别为5(the positive class),有999的图片分类为不是5(false negatives),有4422的图片分类为 true positives)。注意: positive或negative依据的是预测的类别
几个描述分类结果的度量标准(metric):
- precision:
预测为真的分类中,真正为真的类别所占的比列
p r e c i s i o n = T P T P + F P precision = \frac{TP}{TP +FP} precision=TP+FPTP
- recall (sensitivity true positive rate(TPR)):
真正为真的分类中,预测为真的类别所占的比列
r e c a l l = T P T P + F N recall = \frac{TP}{TP+FN} recall=TP+FNTP
计算precision和recall
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)
out:
0.6973663460022078
4422 / (1919 +4422)
out:
0.6973663460022078
recall_score(y_train_5, y_train_pred)
out:
0.8157166574432761
4422 / (4422 +999)
out:
0.8157166574432761
预测为5的类别只有大约为70%预测正确,而真正为5的类别只有约81%预测出来。
F1
F1的定义,将precision和recall结合起来,如果precision和recall很高,(这是我们对一个优秀的算法所期待的),那么F1将很高
F 1 = 2 1 p r e c i s i o n + 1 r e c a l l F1 = \frac{2}{\frac{1}{precision} + \frac{1}{recall}} F1=precision1+recall12
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
out:
0.7519129399761946
在一些场合下我们关注precision,而在另一些场合下,我们更关注recall,比如,如果你想训练一个分类器来检测出对孩子而言安全的视频,你更想可以拒绝很多安全的视频(low recall),但是保留的视频最好是全是安全的(high precision),而在另一个场合下,你训练另一个通过商店监控视频分类小偷的分类器,你希望宁可只有30%的precision却必须要有99%的recall
但是却不能同时使两者都很高,增加precision必然伴随着降低recall,反之亦然,被称为precision/recall tradeoff
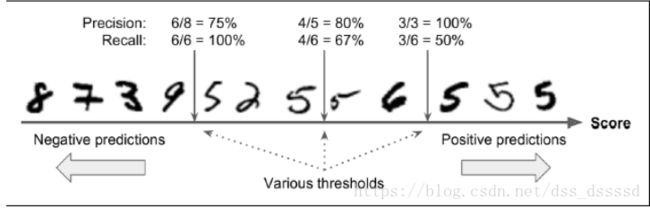
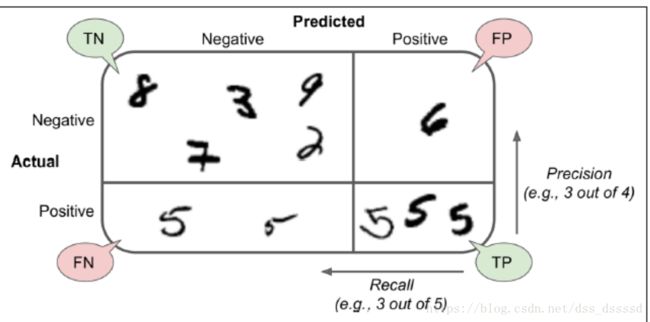
让我们通过上图来了解一下,precision/recall tradeoff:
对于每一个图片,SGDClassifier首先会根据decision function计算一个
分数(score),如果该分数大于某一个阈值(threshold),则分为positive 类,否则分为negative类,首先假设threshold是上图中间的箭头,则此时precision为5个识别为5的手写字体中有4个为5,即4/5=0.8,而真正为5的6个手写字体中识别出来4个,即4/6=0.67,而此时若提高阈值到右边的箭头则,precision=3/3=1,reall=3/6=0.5,同样降低阈值,则提高了recall而降低了precision
设定threshold来分类
sklearn不允许你直接设定阈值(threshold),却允许你通过使用决策分数(decision score)来做预测。
不再调用分类器的predict()函数,调用decision_function()函数,该函数返回的是每一幅图片(每一个实例个体)的分数,接下来基于得到的分数,使用你想设定的阈值来判断
y_scores = sgd_clf.decision_function([some_digits])
y_scores
out:
array([-413834.30335973])
threshold = -600000
y_some_dogit_perd = (y_scores > threshold)
y_some_dogit_perd
out:
array([ True])
SGDClassfier使用的阈值threshold为0,所以返回结果为假
那么,如何确定使用什么阈值呢?仍然使用cross_val_predict()函数,指定method参数为decision_function,获得验证集上所有实例的得分。
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,method="decision_function")
PR曲线
使用得到的分数,对于所有可能的阈值,可以使用precision_recall_curve函数来计算precision和recall
precision_recall_curve 官方文档
使用matplotlib画图片时, 注意precisions和recalls的长度与threshold不一致,大1
from sklearn.metrics import precision_recall_curve
precisions, recalls , threshold = precision_recall_curve(y_train_5, y_scores)
def plot_precision_recall_vs_threshold(precisions, recalls, threshold):
plt.plot(threshold, precisions[:-1 ], "b--", label="Precisions")
plt.plot(threshold, recalls[:-1], "g--", label="Recall")
plt.xlabel("Threshold")
plt.legend(loc="upper left")
plt.ylim([0, 1])
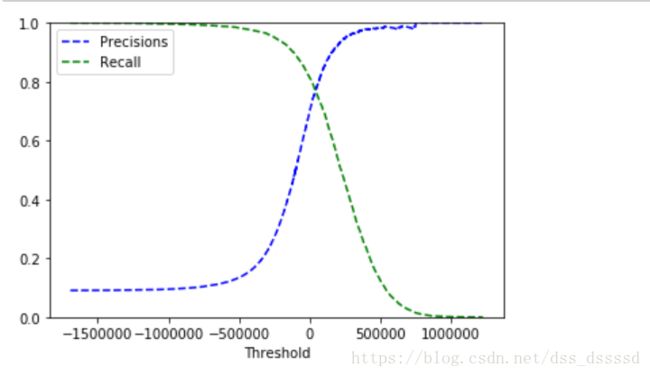
plot_precision_recall_vs_threshold(precisions, recalls, threshold)
plt.show()
注意: 上图中,Precisions的曲线要比Recalls更加不平滑,那是因为当提高阈值时,precision可能会降低,而recall则一定会降低,看一下之前讲述precision和recall的例子,可得,当提高阈值时, 原来识别为5的图片未识别出来导致,precision从4/5=0.8讲到了3/4=0.75.
也可以直接画出precision和recall的变化曲线
def plot_precision_vs_recall(precisions, recalls):
plt.plot(recalls, precisions, "g--")
plt.ylabel("Precision")
plt.xlabel("Recall")
plt.ylim([0, 1])
plt.xlim([0, 1])
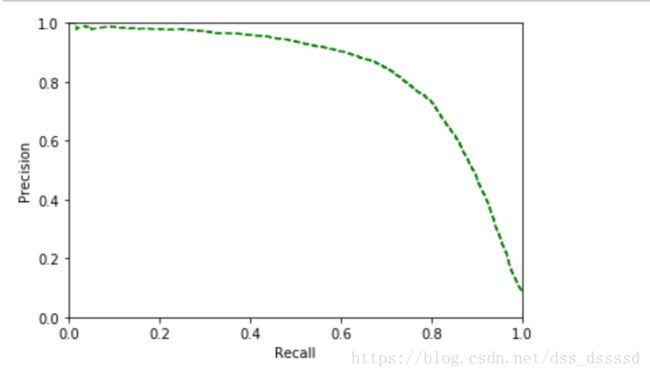
plot_precision_vs_recall(precisions, recalls)
从图中可以看出,recall从60%出开始快速下降,假设选择90%的precision,看第一个图,发现大概threshold大约为65000,此时再预测新的数据时, 不再调用predict()函数,而是先调用decision_function(),获得y_scores,然后使用设定的阈值预测。
y_train_pred_90 = (y_scores > 70000)
# 判断此时的precision和recall
#不幸的是,precision达不到要求
precision_score(y_train_5, y_train_pred_90)
out:
0.8066599394550958
recall_score(y_train_5, y_train_pred_90)
out:
0.7373178380372625
ROC 曲线
ROC曲线(receiever operating characteristic)与precision/recall曲线相似,但刻画的是true positive rate[TPR](recall的另一个名字)和false positive rate[FPR]之间的关系。FPR是错误的被分为正样本的负样本的个数与负样本个数的比值,等于 1 − T N R 1 - TNR 1−TNR;
TNR(true negative rate):负样本中被正确分为负样本的个数与负样本个数的比值,TNR也被称为specificity,因此ROC曲线刻画的是sensitivity(recall)和 1 - specificity之间的关系。
先计算TPR和FPR,使用roc_curve()函数
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
画 ROC 曲线
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0,1], [0,1], 'k--')
plt.axis([0, 1, 0, 1])
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plot_roc_curve(fpr, tpr)
在图中仍然看出tradeoff, 随着recall(TPR)的升高,分类器产生更多的false positive(FPR),虚线代表的是纯随机分类器(purely random classifier),一个好的分类器永远尽可能的远离虚线,尽可能的靠近左上角
AUC
一种类比较分类器好坏的方法是测量AUC(area under the curve),一个完美的分类器AUC = 1,一个纯随机分类的AUC=0.5,可以使用roc_auc_score来计算AUC的值
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
out:
0.956021054307335
既然ROC和PR曲线类似,那使用哪一个呢?
经验法则是,当正样本很少,或者更关心false positives(预测结果将多少负样本预测为正样本) 而非false negatives(预测结果将多少正样本预测为负样本)使用PR, 否则使用ROC。
比如从ROC曲线可以看出分类器表现已经很好,那是因为5的种类要远少于non-5 ,而从PR曲线却可以看出,分类器还可以提升,更加靠近右上角
RandomFroestClassifier
接下来训练一个随机森林的分类器(RandomFroestClassifier),与SGDClassifier比较一下
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
method="predict_proba")
RandonForestClassifier 并没有decision_function()函数,有一个predict_proba()函数,返回的是二维数组,每一个样本为一行,预测的类别为列,每一列中数值为该样本预测属于该类别的概率
前5个样本的概率, 第一列为non-5, 第二列为5
y_probas_forest[:5]
out:
array([[1. , 0. ],
[0.9, 0.1],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ]])
画ROC曲线
要画曲线,需要分数,而非概率,简单的,可以是使用每个实例为5的概率作为分数
y_scores_forest = y_probas_forest[:, 1]
fpr_forest, tpr_forest, threshold_fprest = roc_curve(y_train_5, y_scores_forest)
# 画
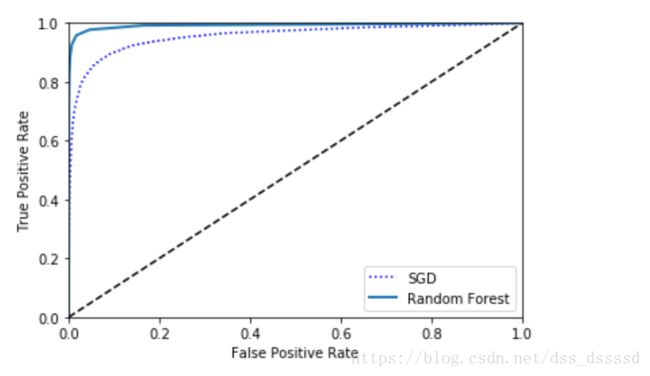
plt.plot(fpr, tpr, "b:", label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.legend(loc="lower right")
从图中看出,随机森林分类器的表现性能更好一点。
AUC得分
roc_auc_score(y_train_5, y_scores_forest)
out:
0.9924050155627879
计算precision和recall
#大于0.5为True, 否则为False
# import numpy as np
# a = np.array([0, 1, 0.7, 0.2])
# a = a > 0.5
# a
y_scores_forest_pred = y_scores_forest > 0.5
precision_score(y_train_5, y_scores_forest_pred)
recall_score(y_train_5, y_scores_forest_pred)
out:
0.9856891237340378
0.8258623870134661
可以看出大约98.5%的precision, 82.8%的recall,模型的表现不算错
三、 Multiclass Classification
至于多类分类器,可以使用Random Forest classifier或者naive Bayes classifier直接进行多类分类,而至于svm和linear classifier则是二元分类器(binary classifier),当然可以使用多个二元分类器来实现多元分类,以上是一些常用的方法。
-
比如要分类0~9,,可以训练10个二元分类器,每一个分类器负责分类一个数字,(0-detector, 1-dector, 2-dector),当要识别一个图片时,利用10个二元分类器预测,分数最高的那个二元分类器就是识别的数字,称为one-versus-all(OvA)strategy, 也叫one-versus-the-rest
-
另一种策略是为每两个数字单独训练一个二元分类器,比如 0s-1s, 1s-2s,2s-3s,比如要区分N类,则需要 N × ( N − 1 ) / 2 N \times (N - 1) / 2 N×(N−1)/2个二元分类器。这被称之为OvO(one-versus-one)strategy, 要分10个数字需要训练45个二元分类器,当要识别一个手写字体时, 将图像分别喂给45个分类器,看一下最后45个分类器的输出结果中哪一个类别占的数量最多,就是哪一类。优点是对于每一个分类器训练时,只需要使用训练集中对应两个类别的数据就好。
对于一些算法(svm)其训练速度及表现会随着训练集的增大而迅速变差,因此对于这些算法,OvO表现的很好,因为相比于在大数据集上训练分类器,在小数据集上训练的速度会更快。但是对于大多数二元分类算法,OvA更好
当使用二元分类算法分类多元任务时,sklearn会自动使用OvA(当使用svm classifer时,使用OvO方法)
使用SGDClassifier分类器在数据及上训练
sgd_clf.fit(X_train, y_train)
# 预测
sgd_clf.predict([some_digits])
out:
array([6.])
实际上sklearn训练了10个二元分类器,得到图像的10个分数,然后分数最高的那个类别是预测结果。
接下来使用decision_function()函数来看一下过程,此时返回的是10个分数
some_digits_scores = sgd_clf.decision_function([some_digits])
some_digits_scores
out:
array([[-595663.21955387, -877340.07369729, -97322.79677218,
-775219.39150077, -187594.85072678, -413834.30335973,
549962.55145472, -604738.90260495, -793937.08372435,
-588881.53014329]])
注意: 当一个分类器在训练时,在class_属性中存储类别的列表,按照值有小到大排序
pos = np.argmax(some_digits_scores)
sgd_clf.classes_
sgd_clf.classes_[pos]
out:
array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
6.0
指定sklearn使用one-versus-one 或者 one-versus-all方法
使用OneVsOneClassifier或者OneVsRestClassifier类,下面是基于SGDClassifier使用OvO方法训练分类器
from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))
ovo_clf.fit(X_train, y_train)
# 预测
pre_dig = ovo_clf.predict([some_digits])
pre_dig
out:
array([6.])
二元分类器的数量
len(ovo_clf.estimators_)
out:
45
随机森林分类器
forest_clf.fit(X_train, y_train)
forest_clf.predict([some_digits])
out:
array([6.])
注意 这次sklearn并没有使用OvO或者OvA,因为随机森林分类器可以直接进行多元分类,使用predict_proba()获得属于各类别的概率
orest_clf.predict_proba([some_digits])
out:
array([[0., 0., 0., 0., 0., 0., 1., 0., 0., 0.]])
当然可以使用cross_val_score()验证算法在验证集上的准确率(accuracy)
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring='accuracy')
out:
array([0.84953009, 0.87074354, 0.84912737])
对输入数据做standardization处理 去均值和方差归一化效果会好一点
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train.shape
out:
(60000, 784)
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring='accuracy')
out:
array([0.90746851, 0.90989549, 0.91048657])
Error Analysis
当然如果是一个真正的项目需要按照以下步骤:数据预处理,实现多个模型,选出最好的模型,使用GridSearchCV来微调超参数,尽可能实现自动化。
在这里,假设已经发现一个好的模型,并且希望继续优化此模型,一种方法是分析预测错误的类型,
首先需要看一下混淆矩阵(confusion matrix),首先使用cross_val_predict()预测,然后调用confusion_matrix()获得混淆矩阵
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx
# out:
'''
array([[5724, 3, 25, 12, 11, 49, 48, 8, 40, 3],
[ 1, 6480, 42, 24, 6, 41, 7, 11, 117, 13],
[ 62, 34, 5333, 96, 83, 23, 93, 54, 166, 14],
[ 46, 42, 138, 5336, 3, 233, 38, 54, 144, 97],
[ 21, 26, 39, 10, 5380, 10, 48, 25, 88, 195],
[ 76, 40, 38, 193, 76, 4592, 108, 34, 175, 89],
[ 38, 25, 44, 1, 38, 90, 5630, 4, 48, 0],
[ 28, 23, 64, 33, 64, 9, 6, 5788, 15, 235],
[ 56, 148, 72, 151, 15, 159, 52, 30, 5033, 135],
[ 47, 27, 30, 83, 175, 35, 3, 214, 74, 5261]],
dtype=int64)
'''
有很多数字,并不直观,我们来看一下confusion matrix的图像表示
plt.matshow(conf_mx, cmap=plt.cm.gray)
混淆矩阵看起来已经很好了,因为大多数图像都在住对角线上,都被正确的分类了。但是5看起来要比其他的数字要暗一些,或许是因为数据集中5的照片较少,也可能是5被正确分类的照片较少。
** 计算错误率:将每行中每一个数除以该行所代表的数字的图像总数(该行的和)**
# 计算行和
row_sums = conf_mx.sum(axis=1, keepdims=True)
row_sums.shape
out:
(10,1)
numpy broadcast
官方文档 https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html
broadcast: 按位+ - * /
两个数组的shape满足以下要求:
- 相等
- 某一维度为1
- 某一个shape的len要小于另一个,但是对于短的那个shape最后到前依次满足上面两条
例子:
Image (3d array): 256 x 256 x 3
Scale (1d array): 3
Result (3d array): 256 x 256 x 3
A (2d array): 5 x 4
B (1d array): 1
Result (2d array): 5 x 4
A (2d array): 5 x 4
B (1d array): 4
Result (2d array): 5 x 4
A (3d array): 15 x 3 x 5
B (3d array): 15 x 1 x 5
Result (3d array): 15 x 3 x 5
A (3d array): 15 x 3 x 5
B (2d array): 3 x 5
Result (3d array): 15 x 3 x 5
A (3d array): 15 x 3 x 5
B (2d array): 3 x 1
Result (3d array): 15 x 3 x 5
计算错误率矩阵
norm_conf_mx = conf_mx / row_sums
要比较错误率,将对角线上用0填充,其余地方越亮表示识别错误率越高
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
注意第8,9列很亮,说明8,9有很多分类错误,同时第8,9行也很亮,说明8,9很容易被分类错误,容易与其他数字混淆,而1都很暗,表明分类很好。
模型性能提升方法
从图中看出,主要通过以下两方面来提升性能
- 提升8和9的分类性能
- 区分3 和5的
解决方法:
- 可以在收集这些数字更多的图像,
- 发掘新的特征, 比如数字闭环的个数(8有2个, 6有1个, 5没有)
- 使用sklearn,pillow, opencv使图像的某些模式更加明显,比如闭环
分析个别错误也可以深入了解分类器如何工作及为何会失败。但是更加困难并且耗时,下面看一下3s和5s
cl_a, cl_b = 3, 5
# 获得四类图像
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = matplotlib.cm.binary, **options)
plt.axis("off")
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
plt.show()
四、 Multilabel Classification 多标签分类
每一个个体输出多个标签,比如,在一个人脸识别系统中,在一张图片中识别多个人,假设分类器被训练识别三个人 Alice, Bob, Charlie;接下来当图片中只有Alice和Charlie,此时输出用为[1, 0,1],即(Alice yes Bob no Charlie yes).
类似这种输出第一个二元标签的分类系统,称为多标签分类系统(multilabel classification system)
看一个简单的例子,
from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
# 按列合并
y_multilabel = np.c_[y_train_large, y_train_odd]
y_multilabel.shape
out:
(60000, 2)
每个个体有两个标签,表示是否大于7和是否为奇数,看一下前3个数据
y_multilabel[:3]
# out
'''
array([[False, False],
[False, False],
[ True, True]])
'''
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)
# 预测 some_digits [6]
knn_clf.predict([some_digits])
# 不大并且为偶数,输出
out:
array([[False, False]])
五、Multioutput Classification
是多标签分类的扩展,对于每一个标签,可能有多个类别(比如有超过两个可能的值)
训练一个从图像中除去噪声的系统,来说明Multioutput Classification。
接受一个有噪声的图片,输出一个去噪后的图片,输出为一维数组,长度为784,注意,分类器的输出是多标签的(每个像素一个标签),并且每个像素的值从0~255变化。
也就是说分类器接受一个图片,输出为长度为784的一维数组,每个值取值为0~255
注意: 分类和回归之间的界限有时候并不会那么清晰,比如在这个例子中,预测像素值更像是一个回归问题,而非分类问题。当然,多输出系统(multioutput system)并不仅仅局限于分类任务,甚至可以在一个系统中为每一个个体输出多个标签,标签包括类标签和值标签(class label and value label)
先创建一个训练集和测试集,其中特征值(x)为在原图像上添加噪声,标签(y)为原图像的值
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
从测试集中找一个图片看一下
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = matplotlib.cm.binary,
interpolation="nearest")
plt.axis("off")
some_index = 500
plt.subplot(121); plot_digit(X_test_mod[some_index])
plt.subplot(122); plot_digit(y_test_mod[some_index])
plt.show()
训练模型然后测试
knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)