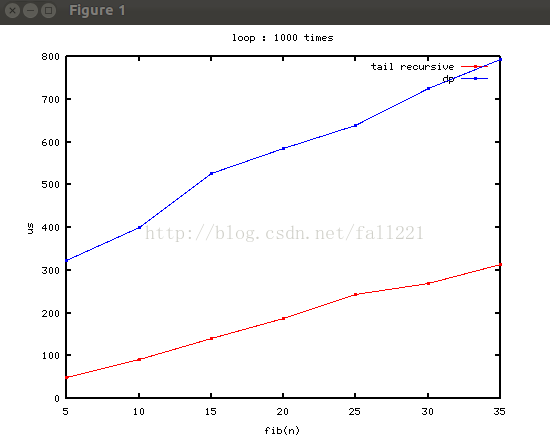
见识一下尾递归的强大!尾递归怎么会比迭代还快!这不科学
1.性能测试
尾递归求Fibonaci数列,三种方法分别是:
(1)普通递归
(2)尾递归
(3)动态规划
第一种重复计算很多,其他两种都能避免重复计算
代码:
#include
#include
//#include
using namespace std;
//using namespace boost;
//using namespace boost::xpressive;
int const N=30;
int const TIMES=1000;
//普通递归
int fib_r(int n)
{ if(n<=1)return 1;
return fib_r(n-1)+fib_r(n-2);
}
//尾递归
int fib_rw(int a, int b, int n)
{
if(n<=1)return b;
return fib_rw(b, a+b, n-1);
}
//动态规划
int fib_dp(int n)
{
int re;
int *p=new int[n+1];
int i;
p[0]=p[1]=1;
for(i=2;i<=n;i++)
p[i]=p[i-1] + p[i-2];
re=p[n];
delete []p;
return re;
}
////// main
int main()
{
struct timeval begin,end;
int re;
////////////////////////
gettimeofday(&begin,0); //尾递归
{
int i=TIMES;
while(--i)
{
re=fib_rw(1,1,N);
}
}
gettimeofday(&end,0);
if(begin.tv_usec>end.tv_usec)
{
end.tv_sec--;
end.tv_usec+=1000000;
}
cout<<"尾递归 "<end.tv_usec)
{
end.tv_sec--;
end.tv_usec+=1000000;
}
cout<<"递归 "<end.tv_usec)
{
end.tv_sec--;
end.tv_usec+=1000000;
}
cout<<"动规 "< 运行一下,计算第30个元素:
chen@chen-book1:~$ g++ a.cpp -o a
chen@chen-book1:~$ ./a
尾递归 1346269 time: 0 s 271 us
递归 1346269 time: 23 s 961794 us
动规 1346269 time: 0 s 424 us
尾递归和动规的曲线:
可见,这两个是线性增长~下面的是尾递归的。
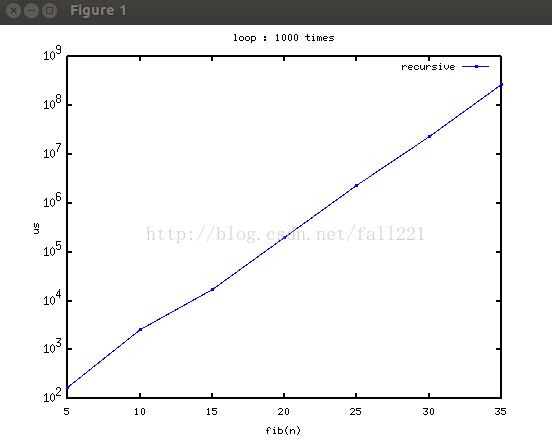
普通递归的曲线:
看到是直的,有没有觉得很高兴?可惜。。纵坐标是对数坐标!标准的指数式增长。。。过了20以后简直要等半天啊。
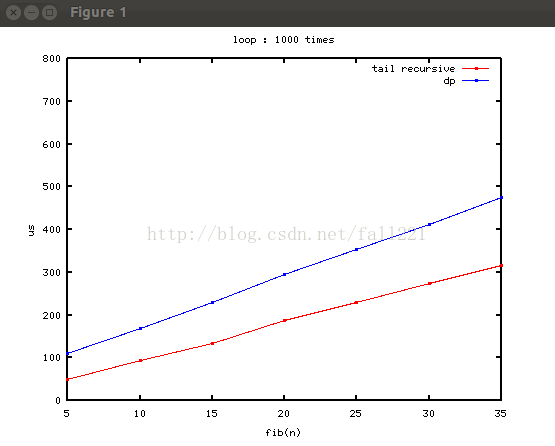
那么,动规为什么比尾递归慢?把new/delete换成静态数组:
将数组声明为全局:
#include
#include
#include
//#include
using namespace std;
//using namespace boost;
//using namespace boost::xpressive;
int const N=20;
int const TIMES=1000;
int p[50]={1,1,};
//普通递归
int fib_r(int n)
{ if(n<=1)return 1;
return fib_r(n-1)+fib_r(n-2);
}
//尾递归
int fib_rw(int a, int b, int n)
{
if(n<=1)return b;
return fib_rw(b, a+b, n-1);
}
//动态规划
int fib_dp(int n)
{
p[0]=p[1]=1;
int i;
for(i=2;i<=n;i++)
p[i]=p[i-1] + p[i-2];
return p[n];
}
////// main
int main(int argc, char*argv[])
{
int N=20;
if(argc>=2)
N=atoi(argv[1]);
struct timeval begin,end;
int re;
////////////////////////
gettimeofday(&begin,0); //尾递归
{
int i=TIMES;
while(--i)
{
re=fib_rw(1,1,N);
}
}
gettimeofday(&end,0);
if(begin.tv_usec>end.tv_usec)
{
end.tv_sec--;
end.tv_usec+=1000000;
}
cout<<"尾递归 "<end.tv_usec)
{
end.tv_sec--;
end.tv_usec+=1000000;
}
cout<<"递归 "<end.tv_usec)
{
end.tv_sec--;
end.tv_usec+=1000000;
}
cout<<"动规 "< 编译运行:
chen@chen-book1:~$ g++ a.cpp -o a
chen@chen-book1:~$ ./a 30
尾递归 1346269 time: 0 s 285 us
动规 1346269 time: 0 s 232 us
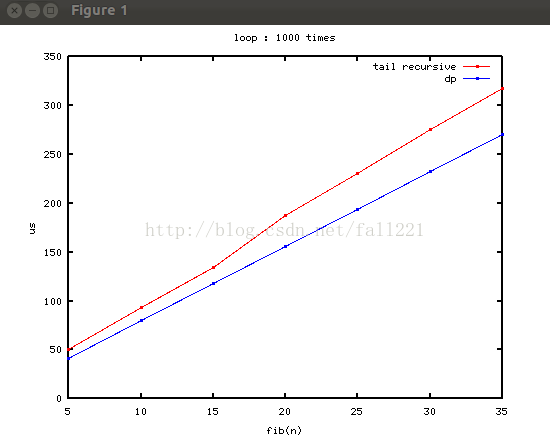
线性性那是杠杠的!这回正常了,动规的迭代比尾递归稍快一点点,但是不多。看来,局部变量的定义也是需要时间的。。。
PS:当然,所谓的动规。。其实是不必要的,完全可以写为:
int fib_dp(int n)
{
int a=1;
int b=1;
int i;
for(i=2;i<=n;i++)
{
b=a+b;
a=b-a;
}
return b;
}
对于没有引进中间变量这件事。。我表示干的很漂亮!。。。当然,本来循环中需要执行一次计算,现在变成两次,时间会上涨那么一点点。。。不过这样空间复杂度就下来了。
2.汇编分析
接下来,要做的事情是。。。分析汇编!
1.先是尾递归的:
(gdb) disas fib_rw
Dump of assembler code for function fib_rw(int, int, int):
0x0804871e <+0>: push ebp
0x0804871f <+1>: mov ebp,esp
0x08048721 <+3>: sub esp,0x18
0x08048724 <+6>: cmp DWORD PTR [ebp+0x10],0x1 n和1比较
0x08048728 <+10>: jg 0x804872f 大于1的话,就jmp到下下下行--->
0x0804872a <+12>: mov eax,DWORD PTR [ebp+0xc] 返回b:eax=b
0x0804872d <+15>: jmp 0x8048750 跳到leave那里
0x0804872f <+17>: mov eax,DWORD PTR [ebp+0x10] --> jmp到这里。n赋值给eax
0x08048732 <+20>: lea edx,[eax-0x1] edx=eax-1
0x08048735 <+23>: mov eax,DWORD PTR [ebp+0xc] eax=b
0x08048738 <+26>: mov ecx,DWORD PTR [ebp+0x8] ecx=a
0x0804873b <+29>: add eax,ecx eax=eax+ecx
0x0804873d <+31>: mov DWORD PTR [esp+0x8],edx esp+8 <-- edx n-1
0x08048741 <+35>: mov DWORD PTR [esp+0x4],eax esp+4 <--a+b
0x08048745 <+39>: mov eax,DWORD PTR [ebp+0xc] eax <-- b
0x08048748 <+42>: mov DWORD PTR [esp],eax
0x0804874b <+45>: call 0x804871e 递归调用
0x08048750 <+50>: leave
0x08048751 <+51>: ret
End of assembler dump.
int fib_rw(int a, int b, int n)
{
if(n<=1)return b;
return fib_rw(b, a+b, n-1);
}
由于参数是 int fib_rw(int a, int b, int n),所以调用的时候:
n入栈 ebp+10
b入栈 ebp+c
a入栈 ebp+8
call的时候,eip入栈 ebp+4
push ebp的时候,ebp入栈,<-----随后,ebp指向这里。所以,[ebp+0x10]指向的是n。从汇编代码来看,每一次调用,栈帧都会sub 0x18,就是二十几个字节。
2.是迭代的
(gdb) disas fib_dp
Dump of assembler code for function fib_dp(int):
0x08048752 <+0>: push ebp
0x08048753 <+1>: mov ebp,esp
0x08048755 <+3>: sub esp,0x10
0x08048758 <+6>: mov DWORD PTR [ebp-0xc],0x1 a
0x0804875f <+13>: mov DWORD PTR [ebp-0x8],0x1 b
0x08048766 <+20>: mov DWORD PTR [ebp-0x4],0x2 i
0x0804876d <+27>: jmp 0x8048788 -->jmp to
0x0804876f <+29>: mov eax,DWORD PTR [ebp-0xc] eax=a -->here
0x08048772 <+32>: add DWORD PTR [ebp-0x8],eax b+=eax b+=a
0x08048775 <+35>: mov eax,DWORD PTR [ebp-0xc] eax=a
0x08048778 <+38>: mov edx,DWORD PTR [ebp-0x8] edx=b
0x0804877b <+41>: mov ecx,edx exc=edx
0x0804877d <+43>: sub ecx,eax ecx - = eax
0x0804877f <+45>: mov eax,ecx eax=ecx
0x08048781 <+47>: mov DWORD PTR [ebp-0xc],eax a=eax
0x08048784 <+50>: add DWORD PTR [ebp-0x4],0x1 i++
0x08048788 <+54>: mov eax,DWORD PTR [ebp-0x4] -->here
0x0804878b <+57>: cmp eax,DWORD PTR [ebp+0x8] ebp+8是输入的n
0x0804878e <+60>: setle al setle是小于等于的比较
0x08048791 <+63>: test al,al
0x08048793 <+65>: jne 0x804876f -->jmp
0x08048795 <+67>: mov eax,DWORD PTR [ebp-0x8]
---Type to continue, or q to quit---
0x08048798 <+70>: leave
0x08048799 <+71>: ret
End of assembler dump.
sub esp,0x10:只用了这么点空间。内存是:
ebp
i=2 ebp-0x4
b=1 ebp-0x8
a=1 ebp-0xc
反正,栈帧是没有发生生长。尾递归比起来,还是具有O(n)的空间复杂度的。迭代则可以避免(如果不用数组的话)