深度学习（Deep Learning）读书思考四：模型训练优化

概述

机器学习应用包括模型构建、求解和评估，对于深度模型而言也是类似，根据之前的介绍可以构建自己的深度神经网络结构。相对于一般的优化问题，深度模型更难优化，本节主要介绍深度学习模型优化挑战、优化算法以及优化策略等。

1. 深度学习模型优化挑战
2. 深度学习优化算法
3. 深度学习中的特殊策略

另外，关于更多数值优化技术可以参考。数值优化技术

深度学习优化挑战

机器学习优化问题

深度学习模型是机器学习模型中一类一种，而一般机器学习优化问题相对于纯优化问题，主要有以下不同：

经验风险最小化

机器学习中优化的终极目标是模型参数能够拟合全部数据，即

min  J(θ)=E(x,y) p(data)L(f(x;θ),y)

然而在大多数情况下，无法获取全部的训练数据或者不知道样本x的分布，因此

机器学习优化问题转化为优化问题采用最简单的思路就是，让模型去更好拟合训练数据。

即

min  J(θ)=E(x,y) p˜(data)L(f(x;θ),y)

该过程也称之为 经验风险最小化。

替代损失函数

有时为了更好的进行模型优化，常常不直接对损失建模，而是采用更容易优化的目标函数进行替代，例如对于0-1损失问题，不是直接采用最小化0-1损失，而是采用sigmoid函数。

minibatch优化算法

minibatch算法是指在优化 J(θ) 的过程中，每次随机选择m个训练样本进行优化，直到达到最优。
该方法在机器学习模型优化中常常被采用，主要原因有：

1. 采用批量或者全量样本进行优化，能够得到准确的梯度，但不是线性关系。例如每次训练时喂入10000个样本和每次100个样本，虽然有100倍关系，但是准确度只能提升大概10倍左右。
2. 采用minibatch方法可以更方便并行，处理更大的样本集合。
3. 能够起到正则化的左右

另外需要注意的是：minibatch算法最好要求每次喂入算法的样本都是随机选择的。

深度学习模型的挑战

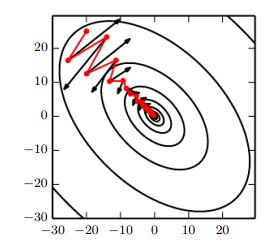
病态条件数

Ill-Conditioning 主要指训练过程中，目标函数值发生抖动，而不是一直下降。通过将目标函数进行二次泰勒展开可以看到学习率对梯度的影响，即每次梯度更新受以下因素影响

12ϵ2gTHg−ϵgTg

虽然可以通过牛顿法进行避免，但是对于深度学习模型而言牛顿方法实施起来比较复杂。

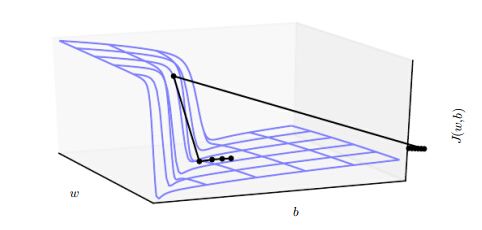
局部最小值

对于非凸优化问题，使用梯度类方法进行优化时常常会导致目标函数常常陷入局部最优解，此时该点的梯度为0，模型参数无法进行自我修正。

鞍点

相对于局部最优问题，鞍点问题在高维优化问题中经常遇到的。鞍点的Hession矩阵既有正的特征值也有负的特征值，此时目标函数值既有可能是最大或者最小值。

梯度爆炸

梯度爆炸是指在某一时刻梯度非常大，可能会导致模型参数变化非常大，好像一个悬崖变化非常剧烈。

1. 该情形在RNN中会经常遇到，特别是设计多个因子相乘的情形。
2. 可以通过启发式策略避免，梯度裁剪策略（Gradient Clipping），是指遇到该情况时，常常忽略最优步长，在最优方向极小的区域内搜索结果。

Long-Term依赖问题

长依赖问题常常会因为多次模型参数相乘，从而导致梯度爆炸或者弥散。

梯度不精确

有些优化目标梯度不存在或者计算复杂度非常高，很多近似梯度计算策略采用，从而导致梯度计算不精确，影响优化精度。

常常通过替代优化目标避免。

深度学习优化算法

基本算法

SGD

随机梯度下降法或者在线优化算法，是优化深度学习模型最常用的技术，伪代码如下：

1. 算法思路非常简单，每次选取m个样本进行计算梯度，进行模型参数优化。
2. 算法中 ϵ 是学习率参数，在实际应用中，学习率更新常常采用如下公式 ϵk=(1−α)ϵ0+αϵτ，其中α=kτ ，即每一轮循环中学习率都衰减，直到第 τ 轮，通常 ϵτ=1%ϵ0
3. 通常采用过度误差（Excess error）度量算法收敛速度， J(θ)−minJ(θ) ，即当前步骤离最优解的距离，SGD的收敛速率为 O(1k√)

Momentum 算法

Momentum 算法在一定情形下能够有效加速学习过程，例如高曲率梯度、一致小的梯度或者带有噪声的梯度，即梯度变化有一定随机的情况。

Momentum算法的主要思路是搜索方向保持一定惯性，累加上之前所有梯度的加权值，模型参数迭代步骤为

v=αv−ϵ∇1m∑L(f(x;θ),y)θ=θ+v

1. α 是一个超参数，实际中常常选择为0.5 0.9 0.99
2. 相比于SGD算法，效果如下，能够一定程度下约束模型参数变化，减少目标值变化范围。
3. Momentum算法是如何加速呢？假设每次参数都是沿着梯度-g进行更新，则 vk=−(αk+αk−1+...+α1)ϵg,根据等比公式有ϵg1−α ，如果超参数选择为0.9则相当于加速10倍。

Nesterov Momentum

相比于标准Momentum算法，他的主要改变在于梯度何时被估计，Nesterov在模型参数v在应用之后在更新模型。公式如下

v=αv−ϵ∇1m∑L(f(x;θ+αv),y)θ=θ+v

参数初始化策略

深度学习模型优化中，模型初始值对结果影响很大，很多情况下需要小心处理。

另外参数初始化还有另外一个重要作用就是避免对称性。

常选择的模型初始方法有：
对于m个输入n个输出的网络结构： U(−1m√,1m√)或者U(−6m+n√,6m+n√)

自适应学习率优化算法

自适应学习率顾名思义：每次迭代，每个模型参数都自适应的改变学习率，而不是所有模型参数都同步修改。

AdaGrad

模型参数的学习率同比例于历史所有梯度的平方和的开方，即更新公式为 ϵi=∑kgi∗gi−−−−−−−−√ ，则优化算法为：

AdaGrad 很多情况下表现较好，并且可以用于其他机器学习算法。

RMSProp

RMSProp算法相比于AdaGrad优势在于处理非凸优化问题，梯度采用指数式方式累加，好处在于更快的遗忘历史梯度影响。更新公式

r=ρr+(1−ρ)g∗g

RMSProp对超参数的噪声也能保持较好的鲁棒性。

优化算法选择

对于大多数问题，采用如下方法即能达到较好的效果，SGD SGD+Momentum、RMSProp、RMSProp+Momentum

高级算法

基础算法主要考虑一阶梯度的影响，对于高级更优的算法会考虑二阶梯度对于目标函数的影响。
常见的算法包括：牛顿法、共轭梯度方法、(L)BFGS等，其主要推导可以参考推荐阅读材料

深度学习优化策略

批量正则化

深度学习模型由于涉及有多个隐藏层，由于梯度爆炸或者弥散问题导致优化难度非常大。另外由于参数量纲不一致，有的特征变化范围比较小，有的特征变化范围比较大，各个维度参数优化效率不一致。
Batch Normalization提供一个优雅的方式对参数重组织，有效解决上述问题。

该思路可以应用于输入或者任何中间层，更新思路如下，H表示输入矩阵，每一行都是一个输入或者隐藏特征。

H′=H−μσμ=∑Hiσ=δ+1m∑(Hi−μ)2−−−−−−−−−−−−−−−−√

通过上述公式对输入进行归一化操作，从而使得参数更新都在统一量纲上。

在测试阶段 μ,σ 可以取训练阶段的均值。

其他策略

还有一些相对比较常用的方法包括
1. 坐标下降方法
2. Polyak Averaging
3. 预训练
4. 模型设计：一个方便优化的模型比使用更大强大的优化算法要好
5. 一些连续方法

总结

通过该小结的学习，可以了解深度学习模型优化的难点，以及常用的优化算法，包括基础算法SGD、Momentum和一些自适应学习算法。另外一些优化策略，特别是Batch Normatization思路。

另外：天下没有免费的午餐，任何强大表达能力更强的算法，都需要小心的进行参数优化；此时不如选择一个更容易优化的模型。这正是奥卡姆剃刀定律的精髓所在。