使用python进行ridge回归

前文我们诊断出三个自变量之间存在严重共线性，那么，我们先使用岭回归，进行建模，然后，使用lasso回归。

岭回归，是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法

通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

先使用R语句如下：

install.packages('ridge')
library(ridge)
rig=linearRidge(y~., data=D) # 这里的D是前文已经定义好的，如果有步明白请再次翻看前文
summary(rig) 

出现报错，不知道是什么原因，在网上找了也没有合适的解决方案，那么咱就不拘泥于一个软件

##########################################

那就使用python

import pandas as pd
data=pd.read_csv('/Users/Documents/train_test_model/ridgereg1.csv') 

#导入数据，数据来源于张文彤spss高级教程中的，婴儿 身长，头围，体重，预测周龄
#三个自变量之间存在严重的共线性，所以，看考虑使用岭回归方法，在spss中，也是需要编程实现的
#所幸的是，python中的sklearn中，实现更加便捷
x_data=data[['long','touwei','weight']] # 定义三个自变量
y_data=data['y']
from sklearn.linear_model import Ridge
ridge=Ridge().fit(x_data,y_data)
print("Training set score:{}".format(ridge.score(x_data,y_data)))
print("ridge.coef_: {}".format(ridge.coef_))
print("ridge.intercept_: {}".format(ridge.intercept_))

#以下就是得到的回归系数，如果没有忘记的话，上面普通逐步回归方法做出来的
#回归系数是 1.692736 -2.158831  0.007472 截距是Intercept 11.011694

#使用岭回归以后的回归系数和截距分别是，合理很多
ridge.coef_: [ 1.32650855 -1.624669    0.00731216]
ridge.intercept_: 10.8370697013
当然你也可以指责我，明明使用了两种不同的软件是否有比较严谨

好了，下面把python线性回归的方法语句贴出来

python实现线性回归语句

import pandas as pd

data=pd.read_csv('/Users/Documentsl/ridgereg.csv')

x_data=data[['long','touwei','weight']] # 定义三个自变量
y_data=data['y']
from sklearn.linear_model import  LinearRegression
lr=LinearRegression().fit(x_data,y_data) 
lr

print("lr.coef_: {}".format(lr.coef_)) # 打印出回归系数
print("lr.intercept_: {}".format(lr.intercept_)) # 打印截距

得到
回归系数: [ 1.69273561 -2.15883088  0.00747203]    

截距: 11.0116943268

对比R实现

回归系数是 1.692736  -2.158831  0.007472  

截距是Intercept 11.011694

抱歉，两种软件在线性回归得到同样的值。

#######################################################################################

正如上文一开始说的，lasso方法也是值得我们试一试的，请看

R实现lasso回归

install.packages("lars")
library(lars)
la<-lars(x,y,type="lar")
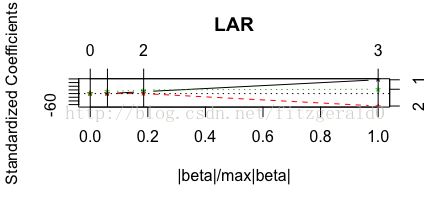
plot(la)
summary(la)

得到：

LARS/LAR
Call: lars(x = x, y = y, type = "lar")
  Df    Rss      Cp
0  1 990.36 712.391
1  2 481.25 337.894
2  3  46.34  18.272
3  4  24.34   4.000

注意这里的 0 指的是截距，第0个模型是只有截距的自变量为常数的模型

根据图可以得到变量选择优先级为x1,x2,x3，再根据cp的值选择的变量为x1,x2,x3。（Cp的选择是选最小的值的模型，这里就是进入了三个自变量的模型3）.

更多关于Mallows' Cp-请自行下载文献：Least squares model averaging by Mallows criterion