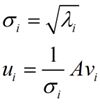机器学习知识点(二十)矩阵奇异值分解基础知识及Java实现
1、奇异值分解基础知识
特征值分解提取矩阵特征只适用于方阵,对于N * M的矩阵要用奇异值分解:
假设A是一个N * M的矩阵,奇异值分解得到的U是一个N * N的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),Σ是一个N * M的矩阵(除了对角线的元素都是0,对角线上的元素称为奇异值),VT(V的转置)是一个N * N的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量)。
通过奇异值如何提取特征值呢?
首先,将一个矩阵A的转置乘以 A,将会得到一个方阵,用这个方阵求特征值可以得到:
v右奇异向量,σ是奇异值,u是左奇异向量。
奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解:
r是一个远小于m、n的数。右边的三个矩阵相乘的结果将会是一个接近于A的矩阵,在这儿,r越接近于n,则相乘的结果越接近于A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵A,如果想要压缩空间来表示原矩阵A,存下这里的三个矩阵:U、Σ、V就可以。
2、Java实现:
还是用jama包实现。
1)测试类:
package sk.ml;
import Jama.SingularValueDecomposition;
import Jama.Matrix;
public class QRTest {
//矩阵特征分解
public static void main(String argv[]){
double[] columnwise = {1.,2.,3.,4.,5.,6.,7.,8.,9.,10.,11.,12.};
Matrix A = new Matrix(columnwise,4);//构造矩阵
A.print(A.getColumnDimension(), A.getRowDimension());
SingularValueDecomposition SVD = A.svd();
Matrix S = SVD.getS();//奇异值
Matrix V = SVD.getV();//右奇异向量
Matrix U = SVD.getU();//左奇异向量
S.print(S.getColumnDimension(), S.getRowDimension());
V.print(V.getColumnDimension(), V.getRowDimension());
U.print(U.getColumnDimension(), U.getRowDimension());
}
}
2)SingularValueDecomposition类源码研究
package Jama;
import Jama.util.*;
/** Singular Value Decomposition.
For an m-by-n matrix A with m >= n, the singular value decomposition is
an m-by-n orthogonal matrix U, an n-by-n diagonal matrix S, and
an n-by-n orthogonal matrix V so that A = U*S*V'.
The singular values, sigma[k] = S[k][k], are ordered so that
sigma[0] >= sigma[1] >= ... >= sigma[n-1].
The singular value decompostion always exists, so the constructor will
never fail. The matrix condition number and the effective numerical
rank can be computed from this decomposition.
*/
public class SingularValueDecomposition implements java.io.Serializable {
/* ------------------------
Class variables
* ------------------------ */
/** Arrays for internal storage of U and V.
@serial internal storage of U.
@serial internal storage of V.
*/
private double[][] U, V;
/** Array for internal storage of singular values.
@serial internal storage of singular values.
*/
private double[] s;
/** Row and column dimensions.
@serial row dimension.
@serial column dimension.
*/
private int m, n;
/* ------------------------
Constructor
* ------------------------ */
/** Construct the singular value decomposition
Structure to access U, S and V.
@param Arg Rectangular matrix
*/
public SingularValueDecomposition (Matrix Arg) {
// Derived from LINPACK code.
// Initialize.
double[][] A = Arg.getArrayCopy();
m = Arg.getRowDimension();
n = Arg.getColumnDimension();
/* Apparently the failing cases are only a proper subset of (m= n"); }
*/
int nu = Math.min(m,n);
s = new double [Math.min(m+1,n)];
U = new double [m][nu];
V = new double [n][n];
double[] e = new double [n];
double[] work = new double [m];
boolean wantu = true;
boolean wantv = true;
// Reduce A to bidiagonal form, storing the diagonal elements
// in s and the super-diagonal elements in e.
int nct = Math.min(m-1,n);
int nrt = Math.max(0,Math.min(n-2,m));
for (int k = 0; k < Math.max(nct,nrt); k++) {
if (k < nct) {
// Compute the transformation for the k-th column and
// place the k-th diagonal in s[k].
// Compute 2-norm of k-th column without under/overflow.
s[k] = 0;
for (int i = k; i < m; i++) {
s[k] = Maths.hypot(s[k],A[i][k]);
}
if (s[k] != 0.0) {
if (A[k][k] < 0.0) {
s[k] = -s[k];
}
for (int i = k; i < m; i++) {
A[i][k] /= s[k];
}
A[k][k] += 1.0;
}
s[k] = -s[k];
}
for (int j = k+1; j < n; j++) {
if ((k < nct) & (s[k] != 0.0)) {
// Apply the transformation.
double t = 0;
for (int i = k; i < m; i++) {
t += A[i][k]*A[i][j];
}
t = -t/A[k][k];
for (int i = k; i < m; i++) {
A[i][j] += t*A[i][k];
}
}
// Place the k-th row of A into e for the
// subsequent calculation of the row transformation.
e[j] = A[k][j];
}
if (wantu & (k < nct)) {
// Place the transformation in U for subsequent back
// multiplication.
for (int i = k; i < m; i++) {
U[i][k] = A[i][k];
}
}
if (k < nrt) {
// Compute the k-th row transformation and place the
// k-th super-diagonal in e[k].
// Compute 2-norm without under/overflow.
e[k] = 0;
for (int i = k+1; i < n; i++) {
e[k] = Maths.hypot(e[k],e[i]);
}
if (e[k] != 0.0) {
if (e[k+1] < 0.0) {
e[k] = -e[k];
}
for (int i = k+1; i < n; i++) {
e[i] /= e[k];
}
e[k+1] += 1.0;
}
e[k] = -e[k];
if ((k+1 < m) & (e[k] != 0.0)) {
// Apply the transformation.
for (int i = k+1; i < m; i++) {
work[i] = 0.0;
}
for (int j = k+1; j < n; j++) {
for (int i = k+1; i < m; i++) {
work[i] += e[j]*A[i][j];
}
}
for (int j = k+1; j < n; j++) {
double t = -e[j]/e[k+1];
for (int i = k+1; i < m; i++) {
A[i][j] += t*work[i];
}
}
}
if (wantv) {
// Place the transformation in V for subsequent
// back multiplication.
for (int i = k+1; i < n; i++) {
V[i][k] = e[i];
}
}
}
}
// Set up the final bidiagonal matrix or order p.
int p = Math.min(n,m+1);
if (nct < n) {
s[nct] = A[nct][nct];
}
if (m < p) {
s[p-1] = 0.0;
}
if (nrt+1 < p) {
e[nrt] = A[nrt][p-1];
}
e[p-1] = 0.0;
// If required, generate U.
if (wantu) {
for (int j = nct; j < nu; j++) {
for (int i = 0; i < m; i++) {
U[i][j] = 0.0;
}
U[j][j] = 1.0;
}
for (int k = nct-1; k >= 0; k--) {
if (s[k] != 0.0) {
for (int j = k+1; j < nu; j++) {
double t = 0;
for (int i = k; i < m; i++) {
t += U[i][k]*U[i][j];
}
t = -t/U[k][k];
for (int i = k; i < m; i++) {
U[i][j] += t*U[i][k];
}
}
for (int i = k; i < m; i++ ) {
U[i][k] = -U[i][k];
}
U[k][k] = 1.0 + U[k][k];
for (int i = 0; i < k-1; i++) {
U[i][k] = 0.0;
}
} else {
for (int i = 0; i < m; i++) {
U[i][k] = 0.0;
}
U[k][k] = 1.0;
}
}
}
// If required, generate V.
if (wantv) {
for (int k = n-1; k >= 0; k--) {
if ((k < nrt) & (e[k] != 0.0)) {
for (int j = k+1; j < nu; j++) {
double t = 0;
for (int i = k+1; i < n; i++) {
t += V[i][k]*V[i][j];
}
t = -t/V[k+1][k];
for (int i = k+1; i < n; i++) {
V[i][j] += t*V[i][k];
}
}
}
for (int i = 0; i < n; i++) {
V[i][k] = 0.0;
}
V[k][k] = 1.0;
}
}
// Main iteration loop for the singular values.
int pp = p-1;
int iter = 0;
double eps = Math.pow(2.0,-52.0);
double tiny = Math.pow(2.0,-966.0);
while (p > 0) {
int k,kase;
// Here is where a test for too many iterations would go.
// This section of the program inspects for
// negligible elements in the s and e arrays. On
// completion the variables kase and k are set as follows.
// kase = 1 if s(p) and e[k-1] are negligible and k= -1; k--) {
if (k == -1) {
break;
}
if (Math.abs(e[k]) <=
tiny + eps*(Math.abs(s[k]) + Math.abs(s[k+1]))) {
e[k] = 0.0;
break;
}
}
if (k == p-2) {
kase = 4;
} else {
int ks;
for (ks = p-1; ks >= k; ks--) {
if (ks == k) {
break;
}
double t = (ks != p ? Math.abs(e[ks]) : 0.) +
(ks != k+1 ? Math.abs(e[ks-1]) : 0.);
if (Math.abs(s[ks]) <= tiny + eps*t) {
s[ks] = 0.0;
break;
}
}
if (ks == k) {
kase = 3;
} else if (ks == p-1) {
kase = 1;
} else {
kase = 2;
k = ks;
}
}
k++;
// Perform the task indicated by kase.
switch (kase) {
// Deflate negligible s(p).
case 1: {
double f = e[p-2];
e[p-2] = 0.0;
for (int j = p-2; j >= k; j--) {
double t = Maths.hypot(s[j],f);
double cs = s[j]/t;
double sn = f/t;
s[j] = t;
if (j != k) {
f = -sn*e[j-1];
e[j-1] = cs*e[j-1];
}
if (wantv) {
for (int i = 0; i < n; i++) {
t = cs*V[i][j] + sn*V[i][p-1];
V[i][p-1] = -sn*V[i][j] + cs*V[i][p-1];
V[i][j] = t;
}
}
}
}
break;
// Split at negligible s(k).
case 2: {
double f = e[k-1];
e[k-1] = 0.0;
for (int j = k; j < p; j++) {
double t = Maths.hypot(s[j],f);
double cs = s[j]/t;
double sn = f/t;
s[j] = t;
f = -sn*e[j];
e[j] = cs*e[j];
if (wantu) {
for (int i = 0; i < m; i++) {
t = cs*U[i][j] + sn*U[i][k-1];
U[i][k-1] = -sn*U[i][j] + cs*U[i][k-1];
U[i][j] = t;
}
}
}
}
break;
// Perform one qr step.
case 3: {
// Calculate the shift.
double scale = Math.max(Math.max(Math.max(Math.max(
Math.abs(s[p-1]),Math.abs(s[p-2])),Math.abs(e[p-2])),
Math.abs(s[k])),Math.abs(e[k]));
double sp = s[p-1]/scale;
double spm1 = s[p-2]/scale;
double epm1 = e[p-2]/scale;
double sk = s[k]/scale;
double ek = e[k]/scale;
double b = ((spm1 + sp)*(spm1 - sp) + epm1*epm1)/2.0;
double c = (sp*epm1)*(sp*epm1);
double shift = 0.0;
if ((b != 0.0) | (c != 0.0)) {
shift = Math.sqrt(b*b + c);
if (b < 0.0) {
shift = -shift;
}
shift = c/(b + shift);
}
double f = (sk + sp)*(sk - sp) + shift;
double g = sk*ek;
// Chase zeros.
for (int j = k; j < p-1; j++) {
double t = Maths.hypot(f,g);
double cs = f/t;
double sn = g/t;
if (j != k) {
e[j-1] = t;
}
f = cs*s[j] + sn*e[j];
e[j] = cs*e[j] - sn*s[j];
g = sn*s[j+1];
s[j+1] = cs*s[j+1];
if (wantv) {
for (int i = 0; i < n; i++) {
t = cs*V[i][j] + sn*V[i][j+1];
V[i][j+1] = -sn*V[i][j] + cs*V[i][j+1];
V[i][j] = t;
}
}
t = Maths.hypot(f,g);
cs = f/t;
sn = g/t;
s[j] = t;
f = cs*e[j] + sn*s[j+1];
s[j+1] = -sn*e[j] + cs*s[j+1];
g = sn*e[j+1];
e[j+1] = cs*e[j+1];
if (wantu && (j < m-1)) {
for (int i = 0; i < m; i++) {
t = cs*U[i][j] + sn*U[i][j+1];
U[i][j+1] = -sn*U[i][j] + cs*U[i][j+1];
U[i][j] = t;
}
}
}
e[p-2] = f;
iter = iter + 1;
}
break;
// Convergence.
case 4: {
// Make the singular values positive.
if (s[k] <= 0.0) {
s[k] = (s[k] < 0.0 ? -s[k] : 0.0);
if (wantv) {
for (int i = 0; i <= pp; i++) {
V[i][k] = -V[i][k];
}
}
}
// Order the singular values.
while (k < pp) {
if (s[k] >= s[k+1]) {
break;
}
double t = s[k];
s[k] = s[k+1];
s[k+1] = t;
if (wantv && (k < n-1)) {
for (int i = 0; i < n; i++) {
t = V[i][k+1]; V[i][k+1] = V[i][k]; V[i][k] = t;
}
}
if (wantu && (k < m-1)) {
for (int i = 0; i < m; i++) {
t = U[i][k+1]; U[i][k+1] = U[i][k]; U[i][k] = t;
}
}
k++;
}
iter = 0;
p--;
}
break;
}
}
}
/* ------------------------
Public Methods
* ------------------------ */
/** Return the left singular vectors
@return U
*/
public Matrix getU () {
return new Matrix(U,m,Math.min(m+1,n));
}
/** Return the right singular vectors
@return V
*/
public Matrix getV () {
return new Matrix(V,n,n);
}
/** Return the one-dimensional array of singular values
@return diagonal of S.
*/
public double[] getSingularValues () {
return s;
}
/** Return the diagonal matrix of singular values
@return S
*/
public Matrix getS () {
Matrix X = new Matrix(n,n);
double[][] S = X.getArray();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
S[i][j] = 0.0;
}
S[i][i] = this.s[i];
}
return X;
}
/** Two norm
@return max(S)
*/
public double norm2 () {
return s[0];
}
/** Two norm condition number
@return max(S)/min(S)
*/
public double cond () {
return s[0]/s[Math.min(m,n)-1];
}
/** Effective numerical matrix rank
@return Number of nonnegligible singular values.
*/
public int rank () {
double eps = Math.pow(2.0,-52.0);
double tol = Math.max(m,n)*s[0]*eps;
int r = 0;
for (int i = 0; i < s.length; i++) {
if (s[i] > tol) {
r++;
}
}
return r;
}
private static final long serialVersionUID = 1;
}