TensorFlow - 循环神经网络(RNN)（NumPy实现）

TensorFlow - 循环神经网络(RNN)（NumPy实现）

flyfish

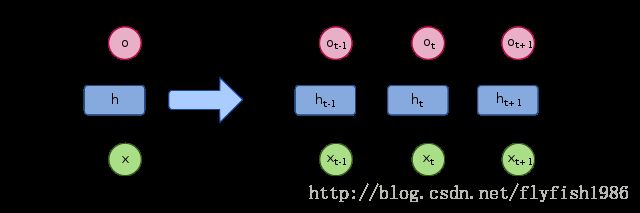
recurrent neural network (RNN)

import numpy as np

#定义参数
X = [1,2]
state = [0.0, 0.0] #隐藏状态被初始化为零向量
#分开定义不同输入部分的权重
w_cell_state = np.asarray([[0.1, 0.2], [0.3, 0.4]])
w_cell_input = np.asarray([0.5, 0.6])
b_cell = np.asarray([0.1, -0.1])
#输出的全连接层参数
w_output = np.asarray([[1.0], [2.0]])
b_output = 0.1

#定义前向传播
for i in range(len(X)):
    #计算循环中的全连接层
    before_activation = np.dot(state, w_cell_state) + X[i] * w_cell_input + b_cell
    state = np.tanh(before_activation)#一个是前一个隐藏状态，一个是基于当前的输入
    #计算当前的输出
    final_output = np.dot(state, w_output) + b_output
    #输出每个时刻的消息
    print ("before activation: ", before_activation)
    print ("state: ", state)
    print ("output: ", final_output)

结果是

before activation:  [0.6 0.5]
state:  [0.53704957 0.46211716]
output:  [1.56128388]
before activation:  [1.2923401  1.39225678]
state:  [0.85973818 0.88366641]
output:  [2.72707101]

np.tanh（双曲正切（hyperbolic tangent））函数是一个非线性函数, 将数据挤压到[-1, 1]之内
为了手工计算方便将state = np.tanh(before_activation)
更改为state = before_activation

before activation:  [0.6 0.5]
state:  [0.6 0.5]
output:  [1.7]
before activation:  [1.31 1.42]
state:  [1.31 1.42]
output:  [4.25]

计算过程

before_activation=[1 * 0.5 + 0.1, 1 * 0.6 - 0.1]
=[0.6,0.5]

state = [0.6, 0.5]
final_output = [0.6*1+0.5*2+0.1]=1.7
--------------------------------------------------------------------------------------
before_activation = [[0.6, 0.5]] 矩阵乘法([[0.1, 0.2], [0.3, 0.4]]) + 2 * ([0.5, 0.6]) + ([0.1, -0.1])
= [0.21, 0.32] + [1.1,1.1]
= [1.31 1.42]
state = [1.31 1.42]
final_output = [1.31,1.42]内积([[1.0], [2.0]]) + 0.1
= [4.25]

dot 函数说明

内积：对于两个一维的数组，计算的是这两个数组对应下标元素的乘积和
矩阵的乘积可以使用dot函数进行计算。对于二维数组，它计算的是矩阵乘积，对于一维数组，它计算的是内积。当需要将一维数组当作列向量或者行向量进行矩阵运算时，可使用reshape函数将一维数组转换为二维数组

代码示例说明
二维的 矩阵与矩阵 矩阵与向量

import numpy as np
a=np.asarray([[1, 2],[3, 4]])
b=np.asarray([[5, 6],[7, 8]])
c=np.asarray([1, 2])

d=np.dot(a,b)
e=np.dot(c,b)
print(d)
print(e)

结果是
d

[[19 22]
 [43 50]]

e

[19 22]

一维的

import numpy as np

c=np.asarray([3, 4])
d= np.asarray([[1.0], [2.0]])
b= np.asarray([1.0, 2.0])


e=np.dot(c,b)
f=np.dot(c,d)
print(e)
print(f)

结果是

e
11.0

f

[11.]

解释

摘自 《白话深度学习与Tensorflow》 Yang Eninala 知乎

假设我手里有三个不同的骰子。
第一个骰子是我们平时常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6 。
第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是 1/4。
第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8 。
当然，用其他点数的骰子原理是一样的。
三种骰子和掷骰子可能产生的结果
D6:1、2、3、4、5、6
D4:1、2、3、4
D8:1、2、3、4、5、6、7、8

假设我们进行下面这个过程，先随机选择一个骰子，然后再用它掷出一个数字，并记录下这个选择和数字。我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3 。然后我们掷骰子，得到一个数字，1、2、3、4、5、6、7、8中的一个。不停地重复上述过程，我们会得到一串数字，每个数字都是1、2、3、4、5、6、7、8中的一个。
例如我们可能得到这么一串数字（掷骰子10次）：1、6、3、5、2、7、3、5、2、4，这串数字叫做可见状态链，也就是我们记录的这组数字，也是我们前面说的On。

但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链。在这个例子里，这串隐含状态链就是我们选出的骰子的序列。比如，隐含状态链有可能是：D6、D8、D8、D6、D4、D8、D6、D6、D4、D8。如果我们继续选取和投掷还能得到这个状态链上更多的节点。一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为实际是隐含状态（所选的骰子）之间存在转换概率（transition probability）。
在我们这个例子里，D6的下一个状态是D4、D6、D8的概率都是1/3 。D4、D8的下一个状态是D4、D6、D8的转换概率也都一样是1/3 ，虽然我们在示例中的10次中没有画出来所有的情况，但是从古典概率的角度来分析，应该是这样，而实际上我们也可以从大量的掷骰子实验中得到这样的转换概率的统计结果。这样设定是为了最开始容易说清楚，其实我们是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。学习的内容，其实是有10个，其中D4有2个，D6有7个，D8有1个，等等。这样就是一个新的HMM，因为转换概率肯定是与我们当前的例子不同的。而同样的，尽管可见状态之间没有直接的转换概率，但是隐含状态和可见状态之间有一个概率叫作输出概率（emission probability）。
就我们的例子来说，六面骰子（D6）产生1的输出概率是1/6 。产生2、3、4、5、6的概率也都是1/6 。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2 ，掷出来是2、3、4、5、6的概率是1/10 。

Xi X i 序列是隐含状态链
Oi O i 序列是可见状态链

训练一个HMM模型是比较容易的，那就是输入这个 Xi X i 序列和这个 Oi O i 序列。最后训练是完全通过统计学模型完成的，而得到的模型结果就是最后这个由D4、D6、D8所组成的转移矩阵。准确说我们得到了两个矩阵，一个是X之间的表示隐含状态转移关系的矩阵，一个是X到O之间的输出概率矩阵。从整个过程来看，隐马尔可夫模型从给予样样本序列到最后训练出来两个矩阵，应该是经历了一个非监督学习过程。
一旦这样的关系得到了，就可以进行一系列的预测工作，例如在知道一次 Xi X i 后判断 Xi X i +1和 Oi O i +1的最大可能性，当然，反推 Xi X i -1和 Oi O i -1也没问题。

在了解到隐马尔可夫模型之后，我们知道了这样一个事实，那就是通过统计的方法可以去观察和认知一个事件序列上临近事件发生的概率转化问题。在RNN模型中是允许模型在训练中去学习这种前后之间的转化影响的，只不过就是在RNN模型中你是无法得到那种标准的隐马尔可夫模型训练中得到的清晰的转化矩阵。