ECCV 2018 Selective Zero-Shot Classification with Augmented Attributes
前两天,看了李宏毅老师的机器学习2019的视频,里面提到了异常检测。深度学习将各种任务的精度提升到了一个高度。但是,想要在实际中应用,会遇到各种问题,比如攻击。给定一个样本,模型能够判定这个样本是个异常样本,而不是随便给定一个标签?
问题: 论文引入了一个选择性零样本分类问题:如何让分类器避免不确定的预测?现有方法在选择性分类场景下性能很差。
分析: 我们认为这是不完备的人类定义属性字典造成的。
方法: 我们提出了一个选择性零样本分类器,基于人类定义属性和自动发现剩余属性。
- 首先,通过联合学习定义和剩余属性,构建提出的分类器。
- 然后,在定义属性子空间执行预测。
- 最后,预测置信度通过定义和剩余属性测量。
度量: 风险-覆盖平衡。
论文下载地址
文章目录
- 1 Introduction
- 2 Related Work
- 2.3 Selective Classification
- 3 Problem Formulation of Selective Zero-Shot Classification
- 4 The Proposed Selective Zero-Shot Classifier
- 4.1 Zero-Shot Classifier $f$ 零样本分类器
- 4.2 Confidence Function 信心函数
- 5 Augmented Attribute Learning
- 6 Experiments
- 6.1 Datasets and Settings
- 6.2 Ablation Study 消融实验
- 7 Conclusions and Future Work
1 Introduction
已见类,未见类是指什么?
零样本分类(ZSC)解决的是识别新类的图片,这些新类在训练中并没有见过。见或者不见,指的是模型见没见过。
选择性分类场景是什么?
选择性分类通过拒绝/丢掉低于置信度阈值的样本来提升分类准确率,以此来降低错误分类的风险。选择性分类包含两个部分:分类器、置信度函数。
为什么选择性分类在ZSC中很重要?
- ZSC不如全监督分类精度高,所以在Selective ZSC中更难。
- 实验6.3中说明,现有ZSC方法没有自我意识。【不能判断预测的置信度】
- 选择性分类在实际中很重要,但是在Selective ZSC中还在研究中。
关于分类:
论文通过字典学习扩增属性,得到由定义属性和剩余属性定义的增强属性空间。但是,论文中只使用定义属性来进行分类,没有用剩余属性。
其实,Discriminative Learning of Latent Features for Zero-Shot Recognition中分类是用的定义属性+隐含属性。
关于置信度函数:
置信度函数包含两个:一个是在定义属性上产生的置信度函数;一个是基于定义属性和剩余属性一致性的置信度函数。
2 Related Work
2.3 Selective Classification
背景:最近几年AI研究社区很关注安全问题。研究者发现深度神经网络很容易被对抗样本欺骗。跟随他们的工作,许多方法提出构建更鲁棒的分类器。
在选择性分类中,不同分类器的置信度分数定义方式不同。生成式分类模型是概率的,自然能提供置信度分数。但是,判别式分类模型不能直接得到预测的概率,而是使用分概率分数,如SVM分类器中的间隔、深度神经网络中的softmax输出。
在这篇论文中,我们提出利用剩余属性来补充定义属性的局限,使得分类器更有自我意识。
3 Problem Formulation of Selective Zero-Shot Classification
选择性分类器:( f , g f, g f,g),其中 f f f是一个标准的零样本分类器, g : X ↦ { 0 , 1 } g: \mathcal{X} \mapsto \{0, 1\} g:X↦{0,1}是一个选择性函数,一般定义为 g ( x ) = 1 { c o n f ( x ) > τ } g(x) = 1 \{conf(x) > \tau \} g(x)=1{conf(x)>τ},conf是置信度函数 τ \tau τ是置信度阈值,1是指示函数。给定一个样本 x \rm {x} x,
(1) ( f , g ) ≜ { f ( x ) , g ( x ) = 1 r e j e c t , g ( x ) = 0 (f,g) \triangleq \left\{ \begin{aligned} f(x), & & g(x)=1 \\ reject, & & g(x)=0 \end{aligned} \tag{1} \right. (f,g)≜{f(x),reject,g(x)=1g(x)=0(1)
4 The Proposed Selective Zero-Shot Classifier
4.1 Zero-Shot Classifier f f f 零样本分类器
给定一张测试图像的预测属性的预测值 d ^ \hat d d^,分类器 f f f是通过一定形式的最近邻构建的:
y ^ = arg max k ∈ Y u s i m ( d ^ , d k ) \hat y = \arg \max_{k \in \mathcal{Y}_u} sim(\hat d, d^k) y^=argk∈Yumaxsim(d^,dk)
4.2 Confidence Function 信心函数
(7) c o n f = ( 1 − λ ) c o n f d + λ c o n f r conf = (1-\lambda)conf_d + \lambda conf_r \tag{7} conf=(1−λ)confd+λconfr(7)
信心函数1
人工定义的属性子空间定义了相似度函数sim,预测值的置信度可以定义为如下相似度分数:
(3) c o n f d = s i m ( d ^ , d k ) conf_d = sim(\hat d, d^k) \tag{3} confd=sim(d^,dk)(3)
信息函数2
(6) c o n f d = s i m ( s ^ d , s r ) conf_d = sim(\hat s_d, s_r) \tag{6} confd=sim(s^d,sr)(6)
(4) s d = arg min s { γ 2 ∣ ∣ s ∣ ∣ 2 + 1 2 ∣ ∣ d ^ − D o s ∣ ∣ F 2 } , s_d =\arg \min_s \rm{ \{ \frac \gamma 2||s||^2 + \frac 1 2 || \hat d - D_os ||_F^2 \}, } \tag{4} sd=argsmin{2γ∣∣s∣∣2+21∣∣d^−Dos∣∣F2},(4)
(5) s r = arg min s { γ 2 ∣ ∣ s ∣ ∣ 2 + 1 2 ∣ ∣ r ^ − R o s ∣ ∣ F 2 } . s_r =\arg \min_s \rm{ \{ \frac \gamma 2||s||^2 + \frac 1 2 || \hat r - R_os ||_F^2 \}. } \tag{5} sr=argsmin{2γ∣∣s∣∣2+21∣∣r^−Ros∣∣F2}.(5)
D s D_s Ds训练数据 X s X_s Xs的定义属性标注 D s ∈ R K d × N s D_s \in \mathbb{R}^{K_d \times N_s} Ds∈RKd×Ns; D o D_o Do是已见类$$的定义属性标注 D o ∈ R K d × ∣ Y s ∣ D_o \in \mathbb{R}^{K_d \times |\mathcal{Y}_s|} Do∈RKd×∣Ys∣
给定未见类的一张图片,将测试图片喂给属性预测模型,我们可以得到测试图片的增强属性表示 ( [ d ^ ; r ^ ] ) ([\hat d; \hat r]) ([d^;r^])。用这个属性表示,可以计算两个相似度向量 ( s d , s r ) (s_d, s_r) (sd,sr):其中, s d s_d sd是定义属性的, s r s_r sr是剩余属性。在这些相似度向量中,第 k k k维的值度量了预测属性和第 k k k类属性表示的相似度。
5 Augmented Attribute Learning
论文将增强属性学习任务看作一个字典学习问题。
6 Experiments
6.1 Datasets and Settings
Evaluation Metrics 评价标准
分类器的性能用覆盖率和风险来量化。
覆盖率定义为 X u \mathcal X_u Xu(不可见类的特征空间)中未拒绝区域的概率质量;
(19) c o v e r a g e ( f , g ) ≜ E p [ g ( x ) ] coverage(f, g) \triangleq E_p[g(x)] \tag{19} coverage(f,g)≜Ep[g(x)](19)
( f , g ) (f, g) (f,g)的选择性风险定义如下:
(20) r i s k ( f , g ) ≜ E p [ ℓ ( f ( x ) , y ) g ( x ) ] c o v e r a g e ( f , g ) risk(f, g) \triangleq \frac {E_p[\ell (f(x), y)g(x)]} {coverage(f, g)} \tag{20} risk(f,g)≜coverage(f,g)Ep[ℓ(f(x),y)g(x)](20)
其中, ℓ \ell ℓ定义的是0/1损失。风险可以用来平衡覆盖率。这样,选择性分类器的总体性能可以用风险-覆盖率曲线(Risk-Coverage Curve, RCC)来测量,其中风险被定义为覆盖率的函数。风险覆盖率曲线下面积(Area Under Risk-Coverage Curve, AURCC)通常用来量化性能。
6.2 Ablation Study 消融实验
三条准则的有效性:
考虑1条准则,LAD
考虑2条准则,SZSC − ^- −
考虑3条准则,SZSC,效果最好(AURCC值最低)。

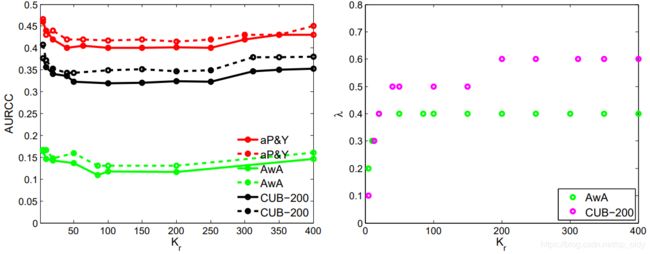
不同的剩余属性的维度,对应的AURCC和 λ \lambda λ变化。 K r K_r Kr越大, λ \lambda λ越大。说明 c o n f r conf_r confr很重要。
7 Conclusions and Future Work
本文研究的题目是一个重要但是没有被研究的问题:零样本分类能够去除不确定的预测值。
本文通过利用剩余属性和定义的属性来设计置信度函数,从而实现更安全的预测。

