实现一层简单神经网络
目录:
一:感知器
二:自适应性线性神经元
视频来源:慕课网http://www.imooc.com/learn/813
正文:
一:感知器
感知器属于监督学习算法类别,更具体地说是单层二值分类器。简而言之,分类器的任务就是基于一组输入变量,预测某个数据点在两个可能类别中的归属。
对于输入信号,经过W的权值进行弱化将信号变小。最后输出到细胞核Z中。而Z不会直接传递出去,而是通过激活函数(即sin或其他函数)进行分类。
如上图的简单激活函数,即大于某个阈值(如0)则输出1,否则输出0.
总体如下图:
其中学习率n需要根据经验来设定。
上图:阈值在开始的时候被当成是W(0),后来每次进行更新
我发现,无论是分类器还是自适应线性神经网络,W(0)和其他的W(1:n)是不一样的计算公式,W(0)是阈值,不需要乘以输入的Xi。
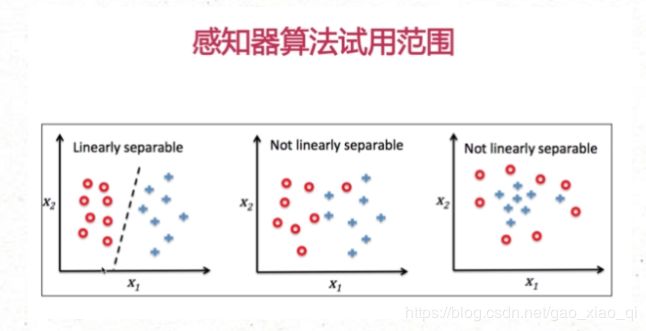
上图:第二第三种是线性不可分割的。
数据越多,权值更新越好,输出结果越准确。
编程:
安装anaconda navigator。(备注:装的是anaconda,里面分别是Anaconda Cloud,Anaconda Navigetor,Anaconda Prompt,IPython,Jupyter Notebook,Jupyter QTCConsole,Reset Spyder Settings,和Spyder。安装和介绍:
http://www.360doc.com/content/16/1029/18/25664332_602357786.shtml)
iris.data.csv数据集粘贴网站:https://wenku.baidu.com/view/2286b7f4f61fb7360b4c6546.html
一个人的博客,里面有大部分代码:http://blog.csdn.net/eric_doug/article/details/51769644?locationNum=9&fps=1
代码实现:
# 包引入
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
df = pd.read_csv("C:/Users/localhost/Desktop/iris.data.csv", header=None)
df.head(10)
y = df.iloc[0:100, 4].values # 预测标签向量
y = np.where(y == 'Iris-setosa', -1, 1)
X = df.iloc[0:100, [0,2]].values # 输入特征向量
# 使用散点图可视化样本
plt.scatter(X[:50, 0], X[:50,1], color='red', marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1], color='blue', marker='x', label='versicolor')
plt.xlabel('petal length')
plt.ylabel('sepal length')
plt.legend(loc='upper left')
plt.show()
class Perceptron(object):
"""
Parameters
------------
eta : float
学习率 (between 0.0 and 1.0)
n_iter : int
迭代次数
Attributes
-----------
w_ : 1d-array
权重
errors_ : list
误差
"""
def __init__(self, eta=0.01, n_iter=10):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
return np.where(self.net_input(X) >= 0.0, 1, -1)
ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X, y)
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of misclassifications')
plt.show()
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.01):
"""
可视化分类器
:param X: 样本特征向量
:param y: 样本标签向量
:param classifier: 分类器
:param resolution: 残差
:return:
"""
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx2.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl)
# 调用可视化分类器函数
plot_decision_regions(X, y, classifier=ppn,resolution=0.02)
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()
结果:由图可知,第6次迭代后,感知器收敛并完美区分出了这两种花。
二:自适应线性神经元:
如果计算的结果(在Activation function)有错误,就会动态的调整参数。如果error大于0,则会返回回来调整W权值参数。不断修正参数。
感知器和自适应性神经元的区别:前面的感知器是分类器,里面的激活函数是步调函数,即当输入的值大于给定的阈值时就输出1,反之输出0.而适应性神经元使用的激活函数(Activation function)将不再是步调函数。而是直接把数据和神经参数相乘后所得的求和结果直接当做最终结果.,并且去跟正确的结果比较来调整权值。
上图第一行的Φ(z)直接等于第二行的Z,y是正确值。通过不断调整W权值,使得距离值:J越来越小。
渐进下降法又名梯度下降法
上图:J有最小值,根据微积分理论,对这个函数求偏导数,当导数大于0,则W需要减少来让J靠近最小值;相反,当导数小于0,说明切线在左边,则应该增加W的值。
上图:η是学习率,前面加负号使上面▽W的公式更加简洁不用加负号。-η=μ;
线性神经元代码实现:
# 包引入
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
df = pd.read_csv("C:/Users/localhost/Desktop/iris.data.csv", header=None)
df.head(10)
y = df.iloc[0:100, 4].values # 预测标签向量
y = np.where(y == 'Iris-setosa', -1, 1)
X = df.iloc[0:100, [0,2]].values # 输入特征向量
# 使用散点图可视化样本
plt.scatter(X[:50, 0], X[:50,1], color='red', marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1], color='blue', marker='x', label='versicolor')
plt.xlabel('petal length')
plt.ylabel('sepal length')
plt.legend(loc='upper left')
plt.show
以上是预备,和前面的分类一样,下面的线性神经元的关键代码实现:
class AdalineGD(object):
"""
eta:float
学习效率,出于0和1之间
n_iter:int
对于训练数据进行学习改进次数
error_:
存储每次迭代改进时,网络对数据进行判断的次数
"""
class AdalineGD(object):
"""
eta:float
学习效率,出于0和1之间
n_iter:int
对于训练数据进行学习改进次数
error_:
存储每次迭代改进时,网络对数据进行判断的次数
"""
def __init__(self,eta=0.01,n_iter=50):
self.eta = eta
self.n_iter = n_iter
def fit(self,X,y):
"""
X:二维数组[n_samples,n_features]
n_samples 表示X中含有训练数据条目数
n_features 含有4个数据的一维向量,用于表示一条训练数目
y:一维向量
用于存储每一训练条目对应的正确分类
"""
self.w_ = np.zeros(1 + X.shape[1])
self.const_ = []
for i in range(self.n_iter):
output = self.net_input(X)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (errors ** 2).sum()/2.0
self.const_.append(cost)
return self
def net_input(self,X):
return np.dot(X,self.w_[1:] + self.w_[0])
def activation(self,X):
return self.net_input(X)
def predict(self,X):
return np.where(self.activation(X) >= 0,1,-1)
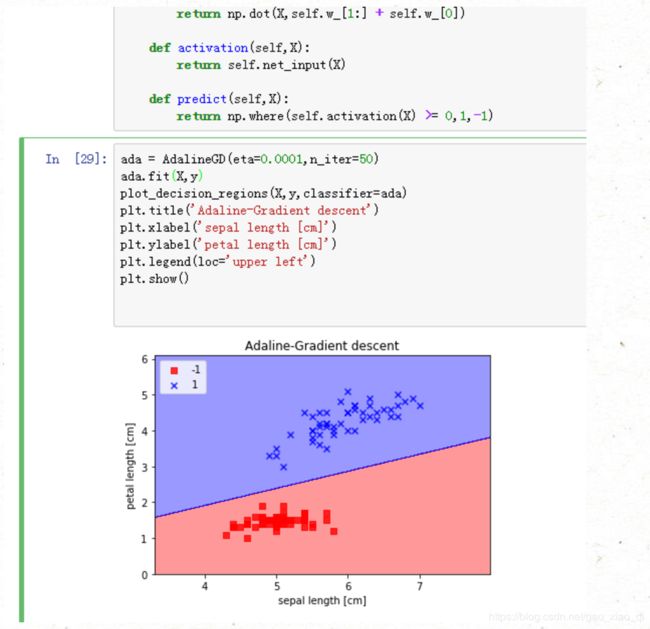
ada = AdalineGD(eta=0.0001,n_iter=50)
ada.fit(X,y)
plot_decision_regions(X,y,classifier=ada)
plt.title('Adaline-Gradient descent')
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()
结果:
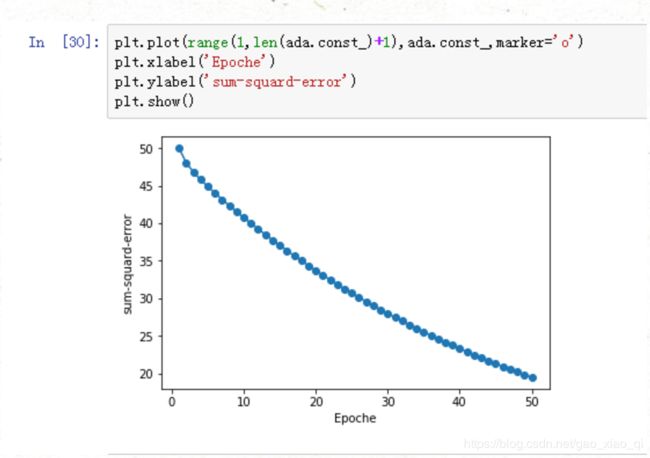
下图:在in[30]中输入的代码,是将在50次迭代的次数中每次将错误次数打印出来,发现模型的error的错误越来越小。
发现一个整理这两个内容和进一步解释用梯度下降算法实现在线学习的文章http://python.jobbole.com/81278/
简单详细的BP算法实现。
http://python.jobbole.com/82758/