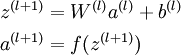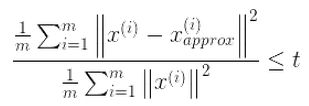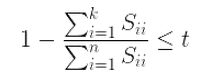深度学习常识

1.overfitting :

线性回归模型 拟合的函数和训练集的关系

1. 图片拟合的函数和训练集误差较大，我们称这种情况为 欠拟合
2. 图片拟合的函数和训练集误差较小，我们称这种情况为 合适拟合
3. 图片拟合的函数完美的匹配训练集数据，我们称这种情况为 过拟合

拿到一个样本，特征非常多，而样例特别少，这样用回归去直接拟合非常困难，容易过度拟合。比如北京的房价：假设房子的特征是（大小、位置、朝向、是否学区房、建造年代、是否二手、层数、所在层数），搞了这么多特征，结果只有不到十个房子的样例。要拟合房子特征‐>房价的这么多特征，就会造成过度拟合。

 如何解决欠拟合和过拟合问题

欠拟合问题，根本的原因是特征维度过少，导致拟合的函数无法满足训练集，误差较大。

欠拟合问题可以通过增加特征维度来解决。

过拟合问题，根本的原因则是特征维度过多，导致拟合的函数完美的经过训练集，但是对新数据的预测结果则较差。

解决过拟合问题，则有2个途径：

1. 减少特征维度; 可以人工选择保留的特征，或者模型选择算法
2. 正则化; 保留所有的特征，通过降低参数θ的值，来影响模型

解决overfitting的方法 

　　dropout， regularization， batch normalizatin，但是要注意dropout只在训练的时候用，让一部分神经元随机失活。 
　　Batch normalization是为了让输出都是单位高斯激活，方法是在连接和激活函数之间加入BatchNorm层，计算每个特征的均值和方差进行规则化。 

　　

防止过拟合的方法 
　　过拟合的原因是算法的学习能力过强；一些假设条件（如样本独立同分布）可能是不成立的；训练样本过少不能对整个空间进行分布估计。 
　　处理方法：

• 早停止：如在训练中多次迭代后发现模型性能没有显著提高就停止训练
• 数据集扩增：原有数据增加、原有数据加随机噪声、重采样
• 正则化
• 交叉验证
• 特征选择/特征降维

2..什麽造成梯度消失问题? 

梯度消失：

这本质上是由于激活函数的选择导致的， 最简单的sigmoid函数为例，在函数的两端梯度求导结果非常小（饱和区），导致后向传播过程中由于多次用到激活函数的导数值使得整体的乘积梯度结果变得越来越小，也就出现了梯度消失的现象。 

梯度爆炸：

同理，出现在激活函数处在激活区，而且权重W过大的情况下。但是梯度爆炸不如梯度消失出现的机会多。 

神经网络的训练中，通过改变神经元的权重，使网络的输出值尽可能逼近标签以降低误差值，训练普遍使用BP算法，核心思想是，计算出输出与标签间的损失函数值，然后计算其相对于每个神经元的梯度，进行权值的迭代。 

梯度消失会造成权值更新缓慢，模型训练难度增加。造成梯度消失的一个原因是，许多激活函数将输出值挤压在很小的区间内，在激活函数两端较大范围的定义域内梯度为0。造成学习停止

3.Backpropagation（要能推倒） 
　　后向传播是在求解损失函数L对参数w求导时候用到的方法，目的是通过链式法则对参数进行一层一层的求导。这里重点强调：要将参数进行随机初始化而不是全部置0，否则所有隐层的数值都会与输入相关，这称为对称失效。 
大致过程是:

• 首先前向传导计算出所有节点的激活值和输出值， 
  

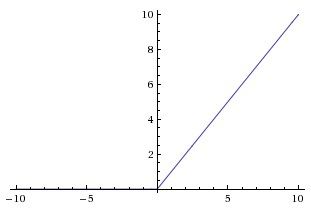
常用的激活函数

几种主要的激活函数：Sigmond / ReLU ／PReLU

激活函数	公式	缺点	优点
Sigmoid	σ(x)=1/(1+e−x)σ(x)=1/(1+e−x)	1、会有梯度弥散 2、不是关于原点对称 3、计算exp比较耗时	-
Tanh	tanh(x)=2σ(2x)−1tanh⁡(x)=2σ(2x)−1	梯度弥散没解决	1、解决了原点对称问题 2、比sigmoid更快
ReLU	f(x)=max(0,x)f(x)=max(0,x)	梯度弥散没完全解决，在（-）部分相当于神经元死亡而且不会复活	1、解决了部分梯度弥散问题 2、收敛速度更快
Leaky ReLU	f(x)=1(x<0)(αx)+1(x>=0)(x)f(x)=1(x<0)(αx)+1(x>=0)(x)	-	解决了神经死亡问题
Maxout	max(wT1x+b1,wT2x+b2)max(w1Tx+b1,w2Tx+b2)	参数比较多,本质上是在输出结果上又增加了一层	克服了ReLU的缺点，比较提倡使用

CNN问题

CNN抓住此共性的手段主要有四个：局部连接／权值共享／池化操作／多层次结构。

• • 局部连接使网络可以提取数据的局部特征；权值共享大大降低了网络的训练难度，一个Filter只提取一个特征，在整个图片（或者语音／文本） 中进行卷积；池化操作与多层次结构一起，实现了数据的降维，将低层次的局部特征组合成为较高层次的特征，从而对整个图片进行表示。
  • 如果每一个点的处理使用相同的Filter，则为全卷积，如果使用不同的Filter，则为Local-Conv。
• 为什么很多做人脸的Paper会最后加入一个Local Connected Conv？
  • 以FaceBook DeepFace 为例：
  • DeepFace 先进行了两次全卷积＋一次池化，提取了低层次的边缘／纹理等特征。
  • 后接了3个Local-Conv层，这里是用Local-Conv的原因是，人脸在不同的区域存在不同的特征（眼睛／鼻子／嘴的分布位置相对固定），当不存在全局的局部特征分布时，Local-Conv更适合特征的提取。

（1） 思想 
　　改变全连接为局部连接，这是由于图片的特殊性造成的（图像的一部分的统计特性与其他部分是一样的），通过局部连接和参数共享大范围的减少参数值。可以通过使用多个filter来提取图片的不同特征（多卷积核）。 
　　 
（2）filter尺寸的选择 
　　通常尺寸多为奇数（1，3，5，7） 
　　 
（3）输出尺寸计算公式 
　　输出尺寸=(N - F +padding*2)/stride + 1 
　　步长可以自由选择通过补零的方式来实现连接。 
　　 
（4）pooling池化的作用 
　　虽然通过.卷积的方式可以大范围的减少输出尺寸（特征数），但是依然很难计算而且很容易过拟合，所以依然利用图片的静态特性通过池化的方式进一步减少尺寸。 池化层降采样(down-sampling)，比如将2x2的图片降为1x1的图片，保留最显著的特征，进一步降低了输出的参数量，并提升模型的畸变容忍能力，提高模型的泛化能力。
　　 
（5）常用的几个模型，这个最好能记住模型大致的尺寸参数。

名称	特点
LeNet5	–没啥特点-不过是第一个CNN应该要知道
AlexNet	引入了ReLU和dropout，引入数据增强、池化相互之间有覆盖，三个卷积一个最大池化+三个全连接层
VGGNet	采用1*1和3*3的卷积核以及2*2的最大池化使得层数变得更深。常用VGGNet-16和VGGNet19
Google Inception Net 我称为盗梦空间网络	这个在控制了计算量和参数量的同时，获得了比较好的分类性能，和上面相比有几个大的改进： 　　1、去除了最后的全连接层，而是用一个全局的平均池化来取代它； 　　2、引入Inception Module，这是一个4个分支结合的结构。所有的分支都用到了1*1的卷积，这是因为1*1性价比很高，可以用很少的参数达到非线性和特征变换。 　　3、Inception V2第二版将所有的5*5变成2个3*3，而且提出来著名的Batch Normalization； 　　4、Inception V3第三版就更变态了，把较大的二维卷积拆成了两个较小的一维卷积，加速运算、减少过拟合，同时还更改了Inception Module的结构。
微软ResNet残差神经网络(Residual Neural Network)	1、引入高速公路结构，可以让神经网络变得非常深 2、ResNet第二个版本将ReLU激活函数变成y=x的线性函数

2、RNN

1、RNN原理： 
　　在普通的全连接网络或CNN中，每层神经元的信号只能向上一层传播，样本的处理在各个时刻独立，因此又被成为前向神经网络(Feed-forward+Neural+Networks)。而在RNN中，神经元的输出可以在下一个时间戳直接作用到自身，即第i层神经元在m时刻的输入，除了（i-1）层神经元在该时刻的输出外，还包括其自身在（m-1）时刻的输出。所以叫循环神经网络 
2、RNN、LSTM、GRU区别

• RNN引入了循环的概念，但是在实际过程中却出现了初始信息随时间消失的问题，即长期依赖（Long-Term Dependencies）问题，所以引入了LSTM。
• LSTM：因为LSTM有进有出且当前的cell informaton是通过input gate控制之后叠加的，RNN是叠乘，因此LSTM可以防止梯度消失或者爆炸。推导forget gate，input gate，cell state， hidden information等因为LSTM有进有出且当前的cell informaton是通过input gate控制之后叠加的，RNN是叠乘，因此LSTM可以防止梯度消失或者爆炸的变化是关键，下图非常明确适合记忆： 
  
• GRU是LSTM的变体，将忘记门和输入们合成了一个单一的更新门。 
  

3、LSTM防止梯度弥散和爆炸 
　　LSTM用加和的方式取代了乘积，使得很难出现梯度弥散。但是相应的更大的几率会出现梯度爆炸，但是可以通过给梯度加门限解决这一问题。 
　　 
4、引出word2vec 
　　这个也就是Word Embedding，是一种高效的从原始语料中学习字词空间向量的预测模型。分为CBOW(Continous Bag of Words)和Skip-Gram两种形式。其中CBOW是从原始语句推测目标词汇，而Skip-Gram相反。CBOW可以用于小语料库，Skip-Gram用于大语料库。具体的就不是很会了。

3、GAN

1、GAN的思想 
　　GAN结合了生成模型和判别模型，相当于矛与盾的撞击。生成模型负责生成最好的数据骗过判别模型，而判别模型负责识别出哪些是真的哪些是生成模型生成的。但是这些只是在了解了GAN之后才体会到的，但是为什么这样会有效呢？ 
　　假设我们有分布Pdata(x)，我们希望能建立一个生成模型来模拟真实的数据分布，假设生成模型为Pg(x;θθ)，我们的目的是求解θθ的值，通常我们都是用最大似然估计。但是现在的问题是由于我们相用NN来模拟Pdata(x)，但是我们很难求解似然函数，因为我们没办法写出生成模型的具体表达形式，于是才有了GAN，也就是用判别模型来代替求解最大似然的过程。 
　　在最理想的状态下，G可以生成足以“以假乱真”的图片G(z)。对于D来说，它难以判定G生成的图片究竟是不是真实的，因此D(G(z)) = 0.5。这样我们的目的就达成了：我们得到了一个生成式的模型G，它可以用来生成图片。

2、GAN的表达式 
 
　　通过分析GAN的表达可以看出本质上就是一个minmax问题。其中V(D, G)可以看成是生成模型和判别模型的差异，而minmaxD说的是最大的差异越小越好。这种度量差异的方式实际上叫做Jensen-Shannon divergence。 
3、GAN的实际计算方法 
　　因为我们不可能有Pdata(x)的分布，所以我们实际中都是用采样的方式来计算差异（也就是积分变求和）。具体实现过程如下： 
 
有几个关键点：判别方程训练K次，而生成模型只需要每次迭代训练一次，先最大化（梯度上升）再最小化（梯度下降）。 
　　但是实际计算时V的后面一项在D(x)很小的情况下由于log函数的原因会导致更新很慢，所以实际中通常将后一项的log(1-D(x))变为-logD(x)。 
　　实际计算的时候还发现不论生成器设计的多好，判别器总是能判断出真假，也就是loss几乎都是0，这可能是因为抽样造成的，生成数据与真实数据的交集过小，无论生成模型多好，判别模型也能分辨出来。解决方法有两个：1、用WGAN 2、引入随时间减少的噪声

4、对GAN有一些改进有引入f-divergence，取代Jensen-Shannon divergence，还有很多，这里主要介绍WGAN

5、WGAN 
　　上面说过了用f-divergence来衡量两个分布的差异，而WGAN的思路是使用Earth Mover distance (挖掘机距离 Wasserstein distance)。

LSTM结构推导，为什么比RNN好？

答案：推导forget gate，input gate，cell state， hidden information等的变化；因为LSTM有进有出且当前的cell informaton是通过input gate控制之后叠加的，RNN是叠乘，因此LSTM可以防止梯度消失或者爆炸；

PCA是一种无监督降维算法，

它是最常用的降维算法之一，可以很好地解决因变量太多而复杂性、计算量增大的弊端。

PCA主成分分析原理

1、协方差原理

　　样本X和样本Y的协方差(Covariance)：

                                        

　　协方差为正时说明X和Y是正相关关系，协方差为负时X和Y是负相关关系，协方差为0时X和Y相互独立。Cov(X,X)就是

X的方差(Variance).当样本是n维数据时，它们的协方差实际上是协方差矩阵（对称方阵），方阵的边长是Cn2。比如对于3

维数据(x,y,z)，计算它的协方差就是：

                                                   

2、SVD分解原理

　　若AX=λX，则称λ是A的特征值，X是对应的特征向量。实际上可以这样理解：矩阵A作用在它的特征向量X上，仅仅使得

X的长度发生了变化，缩放比例就是相应的特征值λ。当A是n阶可逆矩阵时，A与P-1Ap相似，相似矩阵具有相同的特征值。

　　特别地，当A是对称矩阵时，A的奇异值等于A的特征值，存在正交矩阵Q（Q-1=QT），使得：

                                               

　　对A进行奇异值分解就能求出所有特征值和Q矩阵。A∗Q=Q∗D,D是由特征值组成的对角矩阵由特征值和特征向量的定

义知，Q的列向量就是A的特征向量。

3、PCA原理及实现

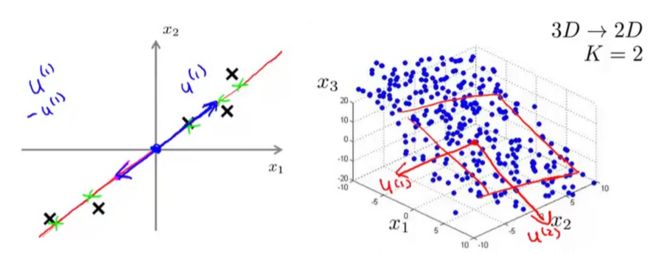
　　PCA主要通过把数据从高维映射到低维来降低特征维度。如下图所示，但映射的时候要保留尽量多的主要信息。

                        

　　PCA的算法步骤如下：

• 输入数据集x={x(1)，x(2)，x(3)，.....，x(m)}、需要降到K维；
• 对所有样本进行均值归一化，如右图所示；　
• 计算协方差矩阵
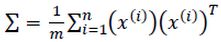
• 对协方差矩阵进行奇异值分解；
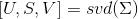• 选取最大的前K个特征值对应的特征向量u(1)，u(2)，u(3)，.....，u(k)
• 输出降维的投影特征矩阵Ureduce={u(1)，u(2)，u(3)，.....，u(k)}
• 输出降维后的数据集z=UreduceTx

4、选择降维后的维度K（主成分的个数）

 　　如何选择主成分个数K呢？先来定义两个概念：

                  

　　选择不同的K值，然后用下面的式子不断计算，选取能够满足下列式子条件的最小K值即可。

                                          

　　其中t值可以由自己定，比如t值取0.01，则代表了该PCA算法保留了99%的主要信息。当你觉得误差需要更小，

你可以把t值设的更小。上式还可以用SVD分解时产生的S矩阵来表示，如下面的式子：

                                                       

注意1：虽然PCA有降维的效果，也许对避免过拟合有作用，但是最好不要用PCA去作用于过拟合。

注意2：在训练集中找出PCA的主成分，（可以看做为映射 mapping），然后应用到测试集和交叉验

证集中。而不是对所有数据集使用PCA然后再划分训练集，测试集和交叉验证集。

 

PCA 的思想

　　将 n维特征映射到 k 维上（k

算法思想：最大方差理论、最小平方误差理论、坐标轴相关度理论

最大方差理论

　　在信号处理中认为信号具有较大的方差， 噪声有较小的方差， 信噪比就是信号与噪声的方差比，越大越好。

最小平方误差理论

假设有这样的二维样本点（红色点），通过线性回归求一个线性函数，使得直线能够最佳拟合样本点。回归时，最小二乘法度量的是样本点到直线的坐标轴距离。

总结与讨论

　　1)   PCA 技术的一大好处，是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维，从而达到简化模型或对数据进行压缩的效果，同时最大程度的保持了原有数据的信息。

　　2)   PCA 技术的一个很大的优点是，它是完全无参数限制的。在 PCA 的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预，最后的结果只与数据相关，与用户是独立的。

　　3)   但是，这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。

　　4)   PCA 还可以用于预测矩阵中缺失的元素。

　　5)   有时数据的分布并不是满足高斯分布。在非高斯分布的情况下，PCA方法得出的主元可能并不是最优的。