台大机器学习基石 Lecture 13 - Hazard of Overfitting

本次Lecture主要介绍机器学习中很重要的问题：过拟合（overfitting），并且介绍了部分解决过拟合问题的方法。

What is Overfitting?

先通过一个例子来介绍bad generalization。

假设平面上有5个点，目标函数是2阶多项式：

• 如果hypothesis是二阶多项式加上一些小的noise的话，那么这5个点很靠近这个hypothesis，很小。
• 如果hypothesis是4阶多项式，那么这5点会完全落在hypothesis上，。
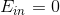• 4阶多项式的必定是小于2阶多项式的，但是它的很大。因为根据VC Bound理论，阶数越大，即VC Dimension越大，就会让模型复杂度更高，更大。

我们把这种很小，很大的情况称之为bad generalization，即泛化能力差。

我们看一下VC曲线：

• 在的时候， 取到最小值；
• 当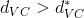也就是向右移动时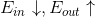，，这就是过拟合（overfitting）；
• 当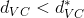也就是向右移动时，，这就是欠拟合（underfitting）。

我们可以理解为，overfitting是VC dimension过大的过程，bad generalization是VC dimension过大的结果。

一个合适的fit则有可能不是特别小，但是能做到和都比较小，这样比overfitting时取得更好的效果，也就是我们不一定要追求特别小的，毕竟我们的目标是。至于underfitting的情况，我们只要逐步提高模型复杂度就可以，相对便于解决。

那么造成overfitting的原因是什么呢？我们把overfit比喻为出车祸：

• 使用过大的（车开太快）
• 存有noise（路面颠簸）
• 数据量N不足（对路况的观察不够）

过大的情况我们知道能逐步提高复杂度来解决，后面主要研究noise 和 N的影响。

The Role of Noise and Data Size

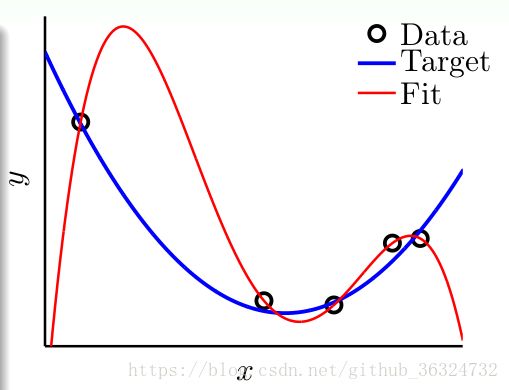
我们看这样一个在二维平面上的例子，离散的圆圈是数据集，目标函数是蓝色的曲线——

• 左图：一个模型的分布由目标函数，是x的10阶多项式。数据没有完全落在曲线上，是因为加入了noise。
• 右图：目标函数是x的50阶多项式，没有noise的情况下，数据就全部落在曲线上。

现在我们分别用二阶多项式和十阶多项式来对两个问题进行拟合，得到下面的结果——

我们能看到在两个问题中，尽管，但。在两个问题中，都发生了过拟合，反而却表现得相对不错。

这似乎与我们的感觉不符：对于目标函数是10阶多项式+noise的问题，凭感觉应该是10阶的模型更能接近于目标函数，因为它们阶数相同。但事实上是2阶模型泛化能力更强。这种现象产生的原因，从哲学上来说，就是“以退为进”。有时候，简单的学习模型反而能表现的更好。

下面我们来看看发生这样现象的具体原因——

以上是用Learning Curves来看两个模型在有noise的情况，关于Learning Curves我们已经在第9节课上讲过了，具体可以复习笔记：台大机器学习基石 Lecture 9 - Linear Regression。和可以表示为：

本节的实验问题中，数据量N不大，即对应于上图中的灰色区域。

• 左图的灰色区域中，因为d=2，和比较接近；
• 右图中的灰色区域中，d=10，很小，而很大；
• 这就解释了之前2阶多项式模型的总是更接近，泛化能力更好。

下面的内容说明了高阶时候的问题，来自redstone的笔记：

但是对于高阶模型，z域中的特征很多的时候，需要的样本数量N很大，且容易发生维度灾难。关于维度灾难的详细生动解释，请参考我另一篇博文：

机器学习中的维度灾难

在第二个noiseless的问题中，我们发现仍然是2阶的模型拟合的效果更好一些，明明没有noise，为什么是这样的结果呢？ 

实际上，我们忽略了一个问题：这种情况真的没有noise吗？其实，当模型很复杂的时候，即50阶多项式的目标函数，无论是2阶模型还是10阶模型，都不能学习的很好，这种复杂度本身就会引入一种‘noise’。所以，这种高阶无noise的问题，也可以类似于10阶多项式的目标函数加上noise的情况，只是二者的noise有所不同，下面将会详细解释。

Deterministic Noise

下面用更具体的例子来说明overfit的发生情况——

假设我们的数据有两部分组成：正常数据 + noise。目标函数是阶多项式，正常数据都正好满足于目标函数，noise是高斯分布的，level记为，数据量为N。我们知道，然后把overfit量化为，越大则表明overfit得厉害。

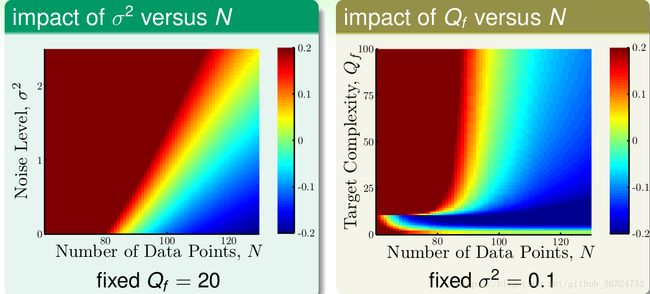
在以上背景下，我们研究和对overfit的影响，结果如下图：

红色越深，代表overfit程度越高，蓝色越深，代表overfit程度越低。

我们能看到关系中，红色区域集中在N很小或者很大的时候，也就是说N越大，越小，越不容易发生overfit。在关系中，红色区域集中在N很小或者很大的时候，也就是说N越大，越小，越不容易发生overfit。

所以，我们发现噪声强度对overfit有很大影响，这被称为随机噪声stochastic noise；模型复杂度对overfit也有很大影响，这被称为固定噪声deterministic noise。

从而，有四个发生overfitting的原因：

• 资料量N太少（data size）
• 随机噪声太多（stochastic noise）
• 模型复杂度太高（deterministic noise）
• 过剩的能力（excessive power），指的是目标函数多项式次数比较低，数据又不够多的时候，这时候就容易使用过高的多项式来拟合，就会产生overfitting（对应的就是上面右图的下部分）。

现在解释deterministic noise的情况，也就是对应着上一节最后的那个问题，为什么目标函数很复杂的时候会被认为是类似存在noise？

我们可以看到上面这幅图中红色的是我们最好的hypothesis，蓝色的是target function，哪怕用最好的hypothesis来拟合仍然会有一些灰色的区域的差距，这些灰色的差距就是deterministic noise。它虽然与stochastic noise原理不同，但是对overfitting来说产生的影响是相同的。

与真正的stochastic noise有什么不同呢？

• deterministic noise依赖于假设集H，如果有一个更复杂的Hypothesis set，那么deterministic noise会变小；
• 对给定的x有同样的deterministic noise，而stochastic noise就是不同的。

这其实就可以理解为， 当我们有一个简单的假设集H的时候，就不要用太复杂的target function，就像教小孩的时候不会用太难的知识一样。

Dealing with Overfitting

现在我们知道了什么是overfitting并且是如何产生的，那么接下来我们来研究如何解决overfitting的问题？主要有四点：

• start from simple model

• data cleaning/pruning

• data hinting

• regularization

• validataion

类比于之前开车的例子就像是这样——

starting from simple model已经讲了很多了，本节主要介绍简单的data cleaning/pruning和data hinting两种方法，regularization和validation两种方法在之后的课程中重点讲解。

• data cleaning/pruning就是对训练数据集里label明显错误的样本进行修正（data cleaning），或者对错误的样本看成是noise，进行剔除（data pruning）。这个方法的重点在于，如何找到错误的label，并且进行处理之后的结果可能也不是很明显（比如处理的点对于整个训练集非常小的时候），效果是不确定的。
• data hinting是针对N不够大的情况，如果获得更多的训练集比较困难，那么data hinting就可以对已知的样本进行简单的处理、变换，从而获得更多的样本。就像是在手写数字辨识中，可以将已知数据轻微平移旋转，这样就能得到更多的数据，这些就是virtual examples，有效地扩充了数据集。这可能有效果，但是必须要注意的是，新的virtual examples要尽量合理，要和原来的数据独立同分布。