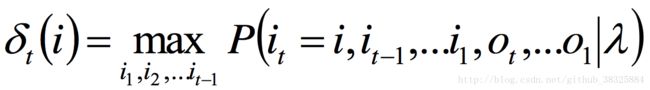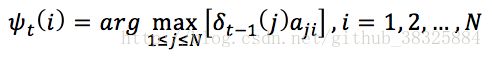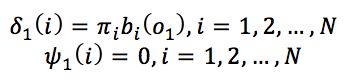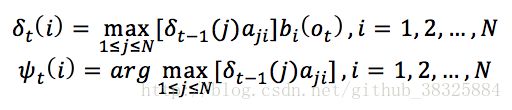隐马尔可夫模型(HMM)
Hidden Markov Model(HMM)是我在QM写硕士毕业论文时研究的算法,相对来讲比较熟悉。当时使用Matlab实现的,Python里面也有相应包,应用起来没什么太大难度。HMM主要是用于对状态进行推测,因此在很多领域里面还是有一定应用的,比如手写识别,中文分词等等。
1. HMM
HMM属于生成模型,是关于时序的概率模型。假设我们现在有一串状态序列Z,对于任意状态![]() ,都存在一个对应的观测
,都存在一个对应的观测![]() ,因此也就存在观测序列X。
,因此也就存在观测序列X。
当![]() 无法观测时,
无法观测时,![]() 和
和![]() 之间就不是独立的,递推可知,X与Z不独立。同理易知
之间就不是独立的,递推可知,X与Z不独立。同理易知![]() 与
与![]() 在
在![]() ,
,![]() 不可观测的情况下也不独立。
不可观测的情况下也不独立。
因此,HMM的模型可以解决样本不独立的问题。对于样本之间存在关系的结构化数据,联合概率并不等于边缘概率的乘积,因此很多模型的前提假设并不满足,在这种情况下,HMM或许是一个很好的选择。一个HMM模型,由初始概率分布![]() ,状态转移概率分布A,以及观测概率分布B确定。设状态Q一共有N种可能,观测V一共有M种可能,状态序列I的长度为T,O是对应的观测序列,则状态转移概率矩阵
,状态转移概率分布A,以及观测概率分布B确定。设状态Q一共有N种可能,观测V一共有M种可能,状态序列I的长度为T,O是对应的观测序列,则状态转移概率矩阵![]() ,其中
,其中![]() 代表的是t时刻,已知状态为
代表的是t时刻,已知状态为![]() 的情况下,t+1时刻状态为
的情况下,t+1时刻状态为![]() 的概率。观测概率矩阵
的概率。观测概率矩阵![]() ,其中
,其中![]() 代表的是t时刻,已知状态为
代表的是t时刻,已知状态为![]() 的情况下,观测结果为
的情况下,观测结果为![]() 的概率。初始概率分布
的概率。初始概率分布![]() 指的其实就是t=1时,状态Q的各个取值的概率。
指的其实就是t=1时,状态Q的各个取值的概率。
HMM的一个经典例子就是李航博士的《统计学习方法》中提到的“盒子和球模型”:假设有4个盒子,每个盒子里都装有红白两种颜色的球,盒子里的红白球如下:
| 盒子 | 1 | 2 | 3 | 4 |
| 红球数 | 5 | 3 | 6 | 8 |
| 白球数 | 5 | 7 | 4 | 2 |
开始时,从四个盒子里一等概率随机选取1个盒子,随机从该盒子里抽出一个球,记录颜色后放回。然后从当前盒子随机转移到下一个盒子,转移规则为:如果当前盒子是1,则下一个盒子一定是2;如果当前盒子是2或3,则分别以0.4和0.6的概率转移到左边和右边的盒子;如果当前盒子是4,则以0.5的概率转移到3,以0.5的概率继续留在4。确定转移后的新盒子之后,继续抽出一个球,记录颜色后放回。重复5次之后,得到一个球的颜色的观测序列:O={红,红,白,白,红}。整个过程无法观测,只能观测最终的球的结果。
这个例子中,盒子的选择序列可以被视作无法观测的状态序列。根据条件,HMM三要素分别表示为:状态集合Q={盒子1,盒子2,盒子3,盒子4},N=4;观测集合V={红,白},M=2;序列长度T=5。
初始概率分布:
状态转移概率分布:
观测概率分布:
2. 观测序列的生成过程
HMM的观测序列O的生成过程,在《统计学习方法》中被描述为:
- 按照初始状态分布
 产生状态
产生状态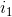
- 令t=1
- 按照状态
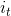 的观测概率分布
的观测概率分布 生成
生成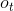
- 按照状态
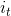 的状态转移概率分布{
的状态转移概率分布{ }产生状态
}产生状态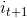 ,
,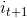 =1,2,...,N
=1,2,...,N - 令t=t+1;如果t
3. HMM的三个核心问题
HMM有三个核心问题:
- The Decoding Problem:已知模型
 及观测序列O,求该情况下使P(I|O)最大的状态序列I
及观测序列O,求该情况下使P(I|O)最大的状态序列I - The Learning Problem:已知观测序列O,使用maximum likelihood估计模型参数A,B,
 使P(O|
使P(O| )最大
)最大 - The Evaluation Problem:给定模型
 和观测序列P,求该模型下观测序列出现的概率P(O|
和观测序列P,求该模型下观测序列出现的概率P(O| )
)
3.1 The Decoding Problem and Viterbi Algorithm
重点说说decoding problem。我在QMUL读硕士的时候,毕业论文做的内容是和自动编曲相关的,当时导师Dr. Dorien Herremans问我懂不懂神经网络,我说不太懂,然后她就推荐了这个复古的HMM给我。HMM在二十世纪基本是自动编曲领域应用的最主流的模型,那个年代还没有深层的神经网络,基本所有论文都是在讨论HMM观测一个什么玩意然后推测对应的状态序列,这个状态序列实际上就是各种和弦。因此HMM在这个领域算得上是功勋卓著的奠基石。
Viterbi Algorithm是由USC的Dr. Andrew Viterbi发明的,Viterbi是Qualcomm的cofounder,专利狂魔,基本上Qualcomm早期通信产品都是靠他撑起来的,学EE的道友肯定不会陌生。这套算法的实质就是DP求概率最大的路径,该路径也就对应着需要求解的状态序列。
如果最优路径在t时刻通过![]() ,则从
,则从![]() 到
到![]() 的这段子路径中,最优路径所走的一定是该子路径集合的最优子路径。因此我们只要从t=1时刻开始DP任何时刻t对应的各个状态i的各条部分路径的最大概率即可。
的这段子路径中,最优路径所走的一定是该子路径集合的最优子路径。因此我们只要从t=1时刻开始DP任何时刻t对应的各个状态i的各条部分路径的最大概率即可。
定义变量![]() :
:
这里的![]() ,指的是t时刻位于状态i的概率最大值。
,指的是t时刻位于状态i的概率最大值。
定义变量![]() :
:
这里的![]() ,指的是使t时刻位于状态i的所有单个路径中概率最大的路径的t-1时刻的状态。
,指的是使t时刻位于状态i的所有单个路径中概率最大的路径的t-1时刻的状态。
初始化![]() 和
和![]() :
:
对t=2,3,...,T进行递推:
求得最优路径在T时刻时的状态:
对t=T-1,T-2,... ,1回溯最终得到最优路径I:
《统计学习方法》中,还给出了一种“近似算法”,大概意思就是对于观测序列中每一个观测值,通过maximum likelihood反求对应的最可能状态值,然后直接将这些对应的状态组成状态序列。这个方法我如果没有理解错的话,应该是一个貌似greedy algorithm的做法。李航博士也在书中说了,会存在无法实现的可能,比如最终的状态序列为(1, 2, 3, 3, 1),可是![]() =0。这个近似算法精度上还是有一些问题的,即使得到可行解,也无法像DP那样保证为global optima。不过正是因为不进行回滚,近似算法的计算更加简单,对于精度要求不高的项目,近似算法依旧是一种高效的堪用算法。
=0。这个近似算法精度上还是有一些问题的,即使得到可行解,也无法像DP那样保证为global optima。不过正是因为不进行回滚,近似算法的计算更加简单,对于精度要求不高的项目,近似算法依旧是一种高效的堪用算法。