机器学习算法(降维)总结及sklearn实践——主成分分析(PCA)、核PCA、LLE、流形学习
降维
- 图谱
- 降维
- 什么时候会用到降维
- 维数灾难
- 降维的主要方法
- 1.投影(Projection)
- 主成分分析(PCA)
- 保留最大方差的超平面
- 主成分(Principle Componets)
- 奇异值分解(SVD)
- 投影到 d 维空间
- Scikit-Learn实现PCA
- 方差解释率(Explained Variance Ratio)
- 核 PCA(Kernel PCA)
- 调整超参数
- 引入模型,通过最优化模型表现调参
- 直接基于最小重建误差搜索最优参数
- 2.流行学习
- 一种流形学习技术——LLE
- 思考和Case实践
- 1. 减少数据集维度的主要动机是什么?主要缺点是什么?
- 2. 什么是维度灾难?
- 3. 一旦对某数据集降维,我们可能恢复它吗?如果可以,怎样做才能恢复?如果不可以,为什么?
- 4. PCA 可以用于降低一个高度非线性对数据集吗?
- 5. 假设你对一个 1000 维的数据集应用 PCA,同时设置方差解释率为 95%,你的最终数据集将会有多少维?
- 6. 在什么情况下你会使用普通的 PCA,增量 PCA,随机 PCA 和核 PCA?
- 7. 你该如何评价你的降维算法在你数据集上的表现?
- 8. 将两个不同的降维算法串联使用有意义吗?
- Case实践
图谱
降维
什么时候会用到降维
分类前,加快训练速度
聚类前,可视化数据
维数灾难
高维数据集有很大风险分布的非常稀疏:大多数训练实例可能彼此远离。当然,这也意味着一个新实例可能远离任何训练实例,这使得预测的可靠性远低于我们处理较低维度数据的预测,因为它们将基于更大的推测(extrapolations)。简而言之,训练集的维度越高,过拟合的风险就越大。
降维的主要方法
降低维度的两种主要方法:投影和流形学习。分别适合以下两种经典数据分布:
1.一个分布接近于2D子空间的3D数据集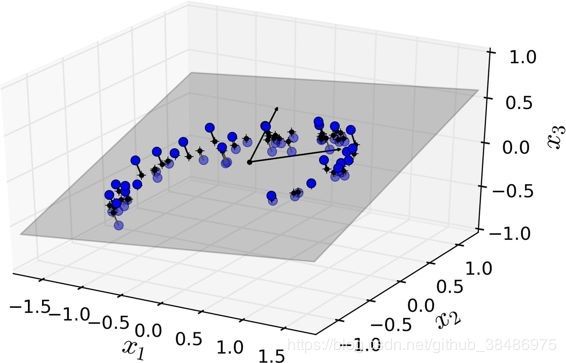
所有训练实例实际上位于(或接近)高维空间的低维子空间内,这样就可以采用投影的降维方法。但是,投影并不总是降维的最佳方法。在很多情况下,子空间可能会扭曲和转动。如下面的数据分布,
2.瑞士卷型数据集
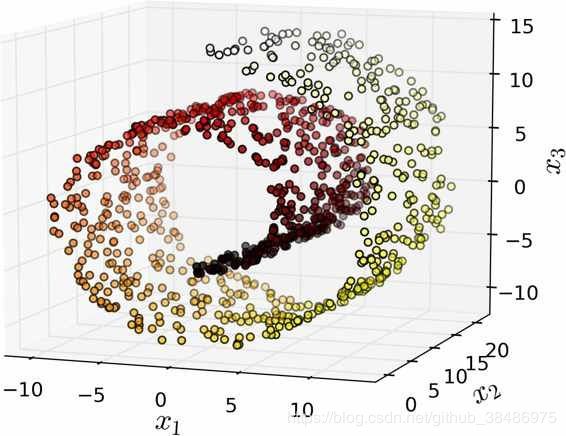
简单地将数据集投射到一个平面上(例如,直接丢弃 x3 )会将瑞士卷层叠在一起,如下图左侧所示。但是,你真正想要的是展开瑞士卷所获取到的类似右侧的 2D 数据集。所以,假设通常包含着另一个隐含的假设:你现在的手上的工作(例如分类或回归)如果在流形的较低维空间中表示,那么它们会变得更简单。如果展开后反而复杂,流形学习便不适用。

1.投影(Projection)
主成分分析(PCA)
主成分分析(Principal Component Analysis)是目前为止最流行的降维算法。首先它找到接近数据集分布的超平面,然后将所有的数据都投影到这个超平面上。
保留最大方差的超平面
例如下图左侧是一个简单的二维数据集,以及三个不同的轴(即一维超平面)。图右边是将数据集投影到每个轴上的结果。正如你所看的,投影到实线上保留了最大方差,而在点线上的投影只保留了非常小的方差,投影到虚线上保留的方差则处于上述两者之间。

选择保持最大方差的轴看起来是合理的,因为它很可能比其他投影损失更少的信息。证明这种选择的另一种方法是,选择这个轴使得将原始数据集投影到该轴上的均方距离最小。这是就 PCA 背后的思想,相当简单。
主成分(Principle Componets)
PCA 寻找训练集中可获得最大方差的轴。如果在一个更高维的数据集中,PCA 也可以找到与前两个轴正交的第三个轴,以及与数据集中维数相同的第四个轴,第五个轴等。 定义第 i 个轴的单位矢量被称为第 i 个主成分(PC)。在上图中,第一个 PC 是 c1 ,第二个 PC 是 c2 。前两个 PC 用平面中的正交箭头表示,第三个 PC 与上述 PC 形成的平面正交(指向上或下)。
奇异值分解(SVD)
那么如何找到训练集的主成分呢?有一种称为奇异值分解(SVD)的标准矩阵分解技术,可以将训练集矩阵 X 分解为三个矩阵 U·Σ·VT的点积,其中 VT =[c1 c2 … cn]包含我们想要的所有主成分。
下面的 Python 代码使用了 Numpy 提供的 svd() 函数获得训练集的所有主成分,然后提取前两个 PC:
X_centered=X-X.mean(axis=0)
U,s,V=np.linalg.svd(X_centered)
c1=V.T[:,0]
c2=V.T[:,1]
警告:PCA 假定数据集以原点为中心。Scikit-Learn 的 PCA 类会自动做中心化处理。但是,自己实现 PCA,或者如果您使用其他库,不要忘记首先要先对数据做中心化处理。
投影到 d 维空间
有了奇异值分解得到的V,任意选取前d个主成分点乘原始数据集便可实现在d维的投影。
下面的 Python 代码将训练集投影到由前两个主成分定义的超平面上:
W2=V.T[:,:2]
X2D=X_centered.dot(W2)
Scikit-Learn实现PCA
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
X2D=pca.fit_transform(X)
可以使用 components_ 访问每一个主成分:
pca.components_.T[:,0]
方差解释率(Explained Variance Ratio)
它表示位于每个主成分轴上的数据集方差的比例
>>> print(pca.explained_variance_ratio_)
array([0.84248607, 0.14631839])
将 n_components 设置为 0.0 到 1.0 之间的浮点数,表明您希望保留的方差比率:
pca=PCA(n_components=0.95)
X_reduced=pca.fit_transform(X)
核 PCA(Kernel PCA)
执行复杂的非线性投影来降低维度,下面的代码使用 Scikit-Learn 的 KernelPCA 类来执行带有 RBF 核的 kPCA
from sklearn.decomposition import KernelPCA
rbf_pca=KernelPCA(n_components=2,kernel='rbf',gamma=0.04)
X_reduced=rbf_pca.fit_transform(X)
调整超参数
由于 kPCA 是无监督学习算法,因此没有明显的性能指标可以帮助您选择最佳的核方法和超参数值。但是,降维通常是监督学习任务(例如分类)的准备步骤.
引入模型,通过最优化模型表现调参
使用 kPCA 将维度降至低维维,然后应用 Logistic 回归进行分类。然后使用 Grid SearchCV 为 kPCA 找到最佳的核和 gamma 值,以便在最后获得最佳的分类准确性.(引入模型,以最优化模型表现调参)
import numpy as np
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
clf = Pipeline([
('ss', StandardScaler()),
("kpca", KernelPCA(n_components=27)),
("log_reg", LogisticRegression())
])
param_grid = [{"kpca__gamma": np.linspace(0.01, 0.05, 10),"kpca__kernel": ["rbf", "sigmoid"]}]
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)
#通过调用 best_params_ 变量来查看使模型效果最好的核和超参数:
print(grid_search.best_params_)#{'kpca__gamma': 0.014444444444444444, 'kpca__kernel': 'rbf'}
直接基于最小重建误差搜索最优参数
由于特征空间是无限维的,我们不能找出重建点,因此我们无法计算真实的重建误差。幸运的是,可以在原始空间中找到一个贴近重建点的点。如果您设置了 fit_inverse_transform = True ,Scikit-Learn 将自动执行此操作:
#用最好参数降维并重建,计算重建误差
rbf_pca = KernelPCA(n_components = 27, kernel="rbf", gamma=0.014,fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)
from sklearn.metrics import mean_squared_error
mean_squared_error(X, X_preimage)#18.690646428102291
基于重建功能,采用交叉验证的方格搜索来寻找可以直接找到最小化重建前图像误差的核方法和超参数:
best_score = 0.0
for gamma in np.linspace(0.01, 0.05, 10):
for kernel in ["rbf", "sigmoid"]:
kpca = KernelPCA(n_components=27,fit_inverse_transform=True)
X_reduced = kpca.fit_transform(X)
X_preimage = kpca.inverse_transform(X_reduced )
score = mean_squared_error(X, X_preimage)
if score > best_score:
best_score = score
best_parameters = {'gamma':gamma,'kernel':kernel}
print(best_parameters,best_score)#{'gamma': 0.01, 'kernel': 'rbf'} 42.0263802221
rbf_pca = KernelPCA(n_components = 27, kernel="rbf", gamma=0.01,fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)
mean_squared_error(X, X_preimage)#18.506800211603057
2.流行学习
瑞士卷一个是二维流形的例子.简而言之,二维流形是一种二维形状,它可以在更高维空间中弯曲或扭曲。
一种流形学习技术——LLE
局部线性嵌入(Locally Linear Embedding)是另一种非常有效的非线性降维(NLDR)方法。
测量每个训练实例与其最近邻(c.n.)之间的线性关系,然后寻找能最好地保留这些局部关系的训练集的低维表示,擅长展开扭曲的流形。
from sklearn.manifold import LocallyLinearEmbedding
lle=LocallyLinearEmbedding(n_components=2,n_neighbors=10)
X_reduced=lle.fit_transform(X)
思考和Case实践
1. 减少数据集维度的主要动机是什么?主要缺点是什么?
•减少维数的主要动机是:
- 加快后续训练算法(在某些情况下甚至可能去除噪声和冗余功能,使训练算法执行更好)。
- 可视化数据。
- 节省空间(压缩)。
•主要缺点是:
- 丢失了一些信息,可能会降低后续性能训练算法。
- 它可能是计算密集型的。1
- 为机器学习流程增加了一些复杂性。
- 转换的过程通常难以解释。
2. 什么是维度灾难?
维度灾难在高维空间中才会出现。一个常见的表现是数据集非常稀疏,增加了过度拟合的风险,在没有充足数据量的情况下难以训练出合适的模型。
3. 一旦对某数据集降维,我们可能恢复它吗?如果可以,怎样做才能恢复?如果不可以,为什么?
一旦对某数据集降维,几乎总是不可能完全恢复它,因为在降维期间某些信息会丢失。此外,而一些算法(如PCA)具有简单的逆向变换过程可以重建与原始数据相对类似的数据集,某些降维算法则没有逆变换的方法(如T-SNE)。
4. PCA 可以用于降低一个高度非线性对数据集吗?
PCA可以显著降低大多数数据集的维数,甚至是高度非线性的数据集,因为它至少可以消除无用特征(维度)的干扰。
但是,如果没有无用的特征(维度),例如,瑞士数据集卷 - 那么使用PCA降低维度会丢失太多信息。你想要展开瑞士卷,而不是挤压它。
5. 假设你对一个 1000 维的数据集应用 PCA,同时设置方差解释率为 95%,你的最终数据集将会有多少维?
这是一个陷阱:它取决于数据集。让我们看看两个极端的例子解释:
首先,假设数据集由几乎完美的点组成对齐。在这种情况下,PCA可以将数据集减少到一个维度同时仍保留95%的差异。
现在想象一下数据集的组成完全随机的点,分散在1000个维度周围。在这种情况下,需要所有1,000个维度来保持95%的方差。
所以答案是,它取决于数据集,它可以是1到1之间的任何数字1000。将解释方差和维数建立联系是一种粗略了解数据集内在维度的方法。
6. 在什么情况下你会使用普通的 PCA,增量 PCA,随机 PCA 和核 PCA?
常规PCA是首选,仅当数据集适合内存时才有效。
增量PCA对于不适合内存的大型数据集很有用,但速度较慢比普通PCA,所以如果数据集适合内存,你应该选择常规PCA。当需要时,增量PCA对在线任务也很有用。每当新实例到达时,PCA即时运行。
随机PCA:当想要大大降低维度并且数据集适合内存时,它比普通PCA快得多。
最后,内核PCA是对非线性数据集很有用。
7. 你该如何评价你的降维算法在你数据集上的表现?
直观地说,如果从数据集中消除了大量维度而不会丢失太多信息,则降维算法表现良好。
衡量这一点的一种方法是应用反向变换并测量重建误差。但是,并非所有降维算法都提供逆向变换。所以,如果构建ML算法模型(例如,随机森林分类器)之前使用降维作为预处理步骤,那么可以简单地评估ML算法模型的性能;如果维数减少没有丢失太多信息,那么ML算法模型的表现应该与使用原始数据集时一样好。
8. 将两个不同的降维算法串联使用有意义吗?
串联两个不同的降维算法绝对有意义。一个常见的例子是使用PCA快速摆脱大量无用的维度,然后应用另一个慢得多的降维算法,如LLE。这种两步法可能会产生与仅使用LLE相同的性能,但只需要很短的时间。
Case实践
-
加载 MNIST 数据集,并将其分成一个训练集和一个测试集(将前60,000 个实例用于训练,其余 10,000 个用于测试)。在数据集上训练一个随机森林分类器,并记录了花费多长时间,然后在测试集上评估模型。接下来,使用 PCA 降低数据集的维度,设置方差解释率为 95%。在降维后的数据集上训练一个新的随机森林分类器,并查看需要多长时间。训练速度更快?接下来评估测试集上的分类器:它与以前的分类器比较起来如何?
-
使用 t-SNE 将 MNIST 数据集缩减到二维,并使用 Matplotlib 绘制结果图。您可以使用10 种不同颜色的散点图来表示每个图像的目标类别。或者,您可以在每个实例的位置写入彩色数字,甚至可以绘制数字图像本身的降维版本(如果绘制所有数字,则可视化可能会过于混乱,因此您应该绘制随机样本或只在周围没有其他实例被绘制的情况下绘制)。你将会得到一个分隔良好的的可视化数字集群。尝试使用其他降维算法,如PCA,LLE 或 MDS,并比较可视化结果。
直接从sklearn中load数据集
# In[直接从sklearn中load数据集]
from sklearn.datasets import load_digits
digits = load_digits(n_class=6)
X = digits.data
y = digits.target
n_samples, n_features = X.shape
print("Dataset consist of %d samples with %d features each" % (n_samples, n_features))
# 绘制数字示意图
n_img_per_row = 20
img = np.zeros((10 * n_img_per_row, 10 * n_img_per_row))
for i in range(n_img_per_row):
ix = 10 * i + 1
for j in range(n_img_per_row):
iy = 10 * j + 1
img[ix:ix + 8, iy:iy + 8] = X[i * n_img_per_row + j].reshape((8, 8))
plt.imshow(img, cmap=plt.cm.binary)
plt.xticks([])
plt.yticks([])
_ = plt.title('A selection from the 8*8=64-dimensional digits dataset')
plt.show()
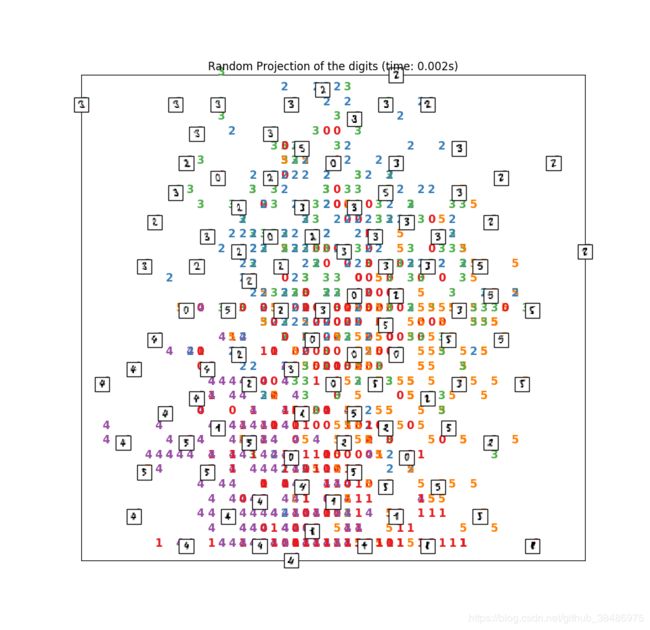
# In[随机投影]
#把数据随机投射到两个维度上
#import所需的package
from sklearn import (manifold, decomposition, random_projection)
rp = random_projection.SparseRandomProjection(n_components=2, random_state=42)
#定义绘图函数
from matplotlib import offsetbox
def plot_embedding(X, title=None):
x_min, x_max = np.min(X, 0), np.max(X, 0)
X = (X - x_min) / (x_max - x_min)
plt.figure(figsize=(10, 10))
ax = plt.subplot(111)
for i in range(X.shape[0]):
plt.text(X[i, 0], X[i, 1], str(digits.target[i]),
color=plt.cm.Set1(y[i] / 10.),
fontdict={'weight': 'bold', 'size': 12})
if hasattr(offsetbox, 'AnnotationBbox'):
# only print thumbnails with matplotlib > 1.0
shown_images = np.array([[1., 1.]]) # just something big
for i in range(digits.data.shape[0]):
dist = np.sum((X[i] - shown_images) ** 2, 1)
if np.min(dist) < 4e-3:
# don't show points that are too close
continue
shown_images = np.r_[shown_images, [X[i]]]
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r),
X[i])
ax.add_artist(imagebox)
plt.xticks([]), plt.yticks([])
if title is not None:
plt.title(title)
#记录开始时间
import time
start_time = time.time()
X_projected = rp.fit_transform(X)
plot_embedding(X_projected, "Random Projection of the digits (time: %.3fs)" % (time.time() - start_time))
# In[PCA降维]
from sklearn import (manifold, decomposition, random_projection)
#TruncatedSVD 是 PCA的一种实现
X_pca = decomposition.TruncatedSVD(n_components=2).fit_transform(X)
#记录时间
start_time = time.time()
plot_embedding(X_pca,"Principal Components projection of the digits (time: %.3fs)" % (time.time() - start_time))
# In[非线性的变换 t-SNE 降维]
#非线性的变换来做降维操作,从原始的64维降到2维空间,效果更好
#这里我们用到一个技术叫做t-SNE,sklearn的manifold对其进行了实现
from sklearn import (manifold, decomposition, random_projection)
#降维
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
start_time = time.time()
X_tsne = tsne.fit_transform(X)
#绘图
plot_embedding(X_tsne,
"t-SNE embedding of the digits (time: %.3fs)" % (time.time() - start_time))
计算密集型是指,每个请求的命令中,大都包含不同的参数值,很难重用前一次计算的结果,所以要按照约定的业务逻辑重新计算,并按照约定的格式返回数据,且计算在总耗时中占比较大。 ↩︎