Coursera上的Andrew Ng《机器学习》学习笔记Week1
Coursera上的Andrew Ng《机器学习》学习笔记Week1
作者:雨水/家辉,日期:2017-01-17,CSDN博客:http://blog.csdn.net/gobitan
注:本课程结合Octave讲解!Octave是类似MATLAB的数值计算软件。
Lecture 1: Introduction
什么是机器学习?
机器学习就是不通过显示地编程而赋予计算机学习的能力。Machine Learning: Field of study that gives computers the ability to learn without being explicitly programmed.
机器学习算法可分为两类:
[1] 有监督学习(Supervised Learning):监督学习通常会预先提供正确的答案
[2] 无监督学习(Unsupervised Learning):无预知答案,聚类,鸡尾酒会问题
有监督学习问题可分为两类:
回归分析(regression):预测持续的输出值
分类(classification):离散的输出值,比如0或者1
无监督学习:聚类等
Lecture 2: Linear Regression with One Variable
2.1 Model & Cost Function
2.1.1 Model Representation
univariate linear regress: 单变量线性回归
2.1.2 Cost Function
Cost Function又称为Lost Function,用于评估回归分析的准确度。
Squared error function 均方误差函数,也称为Mean squared error。基于均方误差最小化进行模型求解的方法称为“最小二乘法(least square method)”。
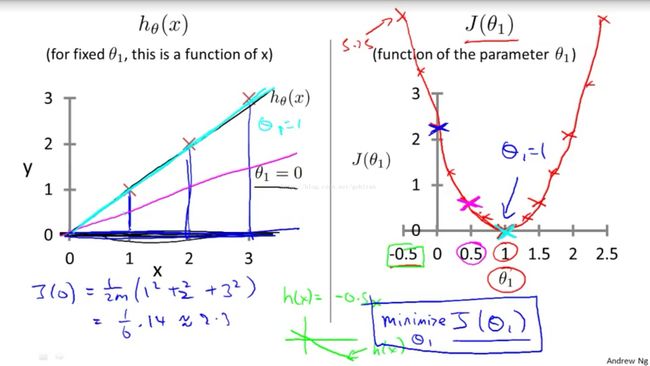
Cost Function Intuition I
本质就是求成本函数最小值,此时的参数就是所期望得到的。
Cost Function Intuition II
contour plot 等高线
2.2 Parameter Learning
2.2.1 Gradient Descent 梯度下降
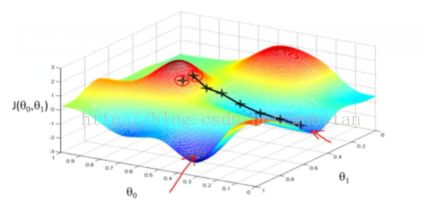
大牛就是大牛,吴恩达(Andrew Ng)的课深入浅出,瞬间就明白了听起来高大上的梯度下降算法。先看看下面这张图。
上面的J成本函数图形化之后就是一个等高线图。为了获得最好的回归参数,就是要得到当成本函数J的值最小的时候的参数的值。由于数学表达式输入极不方便,因此大都以图形代替。且看下面梯度下降算法的表达式:
给定一个初始值,然后不断迭代。初始值就相当于选取了一个初始点,然后沿该点梯度下降的方向不断迭代。因此,初始点的选取决定了局部最优值,这点在上面等高线图上很容易看明白。
下面以单参数θ为例,讲解成本函数J如何收敛的问题。首先,成本函数中有一个α参数,它代表步长,也叫学习频率(learning rate)。这个值如果太大,容易错过最低值,如果太小,算法迭代的速度就比较慢。 α参数后面的部分为J在参数θ位置的导数。如下图所示:
随着梯度的不断下降,后面导数部分的值会越来越小,每步的步长也将变小,因此不用随时间降低α参数的值。
疑问:
[1] 既然梯度下降算法只能收敛到局部最优值,而初始值的选取将决定这个值。那么,如何选取多个初始值,从而获取全局最优值呢?
[2] 既然步长α参数选择太小,迭代数据就太慢。太大的话,容易越过最优值,怎么选择才能兼顾,从而达到不越过最优值的情况下迭代速度最快?注:在week2中有解答
Gradient Descent For Linear Regression
convex function 凸函数
Lecture 3: Linear Algebra Review
矩阵Matrix:Ai,j
向量Vector:yi=ith
矩阵加法:Matrix Addition
矩阵标量乘法:Matrix Scalar Multiplication,Scalar就是real number
Matrix Vector Multiplication
Matrix Matrix Multiplication
Matrix Multiplication Properties
[1] 不具有交换律 not commutative law
[2] 具有结合律 associative law
单位矩阵identity matrix,用I表示
对于任意矩阵A,乘以单位矩阵之后保持不变。如I *A=A*I=A
矩阵的逆inverse和转置矩阵transposed matrix
单个数的逆,比如3乘以3的负一次方=1,即3 * 1/3 = 1。不是所有的数都有逆,比如0.
矩阵逆的定义:If A is an m x m matrix, and if it has an inverse, then, A A-1=A-1 A=I
奇异矩阵(singular matrix)
退化矩阵degenerate matrix
参考资料:
[1] https://www.coursera.org/learn/machine-learning