AVL树的旋转详解
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素也就相当于是在顺序表中搜索元素,效率低下。因此,为了解决二叉搜索树中单支树的这种情况,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了AVL(平衡树):当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差(平衡因子)的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
故AVL树有两个最大的特点:
1、AVL树的左右子树都是也都是平衡树。
2、AVL树的平衡因子(左右子树高度之差)的绝对值不能超过1。
AVL树的介绍就到次,本篇文章主要讲解一下AVL树的四大旋转问题。为了方便理解,本文通过对将一组数插入到AVL树中的具体过程来帮助大家解开旋转的迷雾。
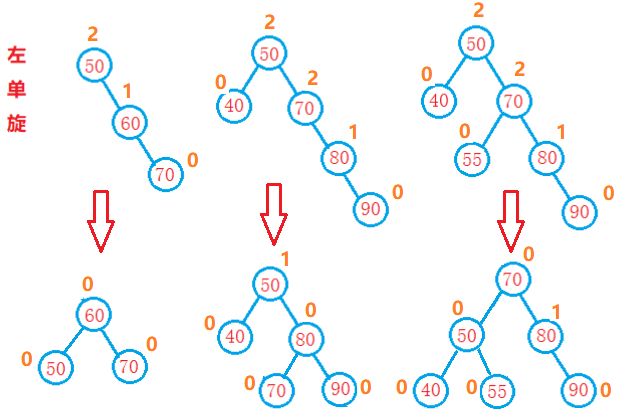
左单旋
当向较高右子树(不一定是根的右子树,也可以是根的左子树中的右子树)的右侧插入一个新的结点时,就会导致右侧的高度比左侧的高度高2,平衡因子失衡。(可以想象自己拿着一条绳子,右边的部分长一些,为了让左边的跟右边的一样长,是不是只要拿着左端往左边扯一下,就可使两端一样长了)同理,此时就需要往左旋转。
左单旋思路:
先判端是否为左单旋的情况,如果是 ---->找到第一个失去平衡的结点,暂将其标记为P----> 将其右孩子标记为 PR ,---->右孩子PR的左子树标记为PRL (可能为NULL,如下图第一种情况);然后使用PR代替原来P的位置 ---->将PR的左子树放在P的右孩子位置 ---->最后将P放到PR的左孩子位置。
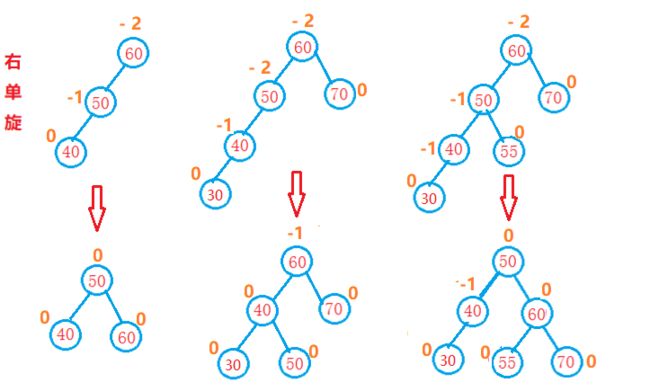
右单旋:
右单旋思路:
先判端是否为右单旋的情况,如果是 ---->找到第一个失去平衡的结点,暂将其标记为P----> 将其右孩子标记为 PL ,---->右孩子PL的右子树标记为PLR (可能为NULL,如下图第一种情况);然后使用PL代替原来P的位置 ---->将PL的右子树放在P的左孩子位置 ---->最后将P放到PL的右孩子位置。
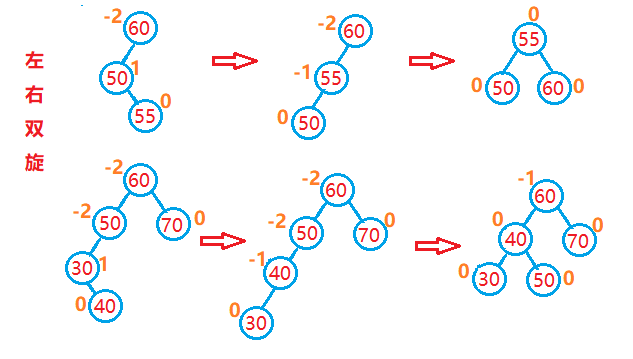
左右双旋:
当在较高左子树的右侧插入一个结点时,导致较高左子树的双亲结点失去平衡。此时是较高左子树的右侧导致的失衡,仅仅
依靠单旋已经没法调整平衡了。
判断是否为左右双旋的情况,如果是--->先使用左单旋,再使用右单旋。
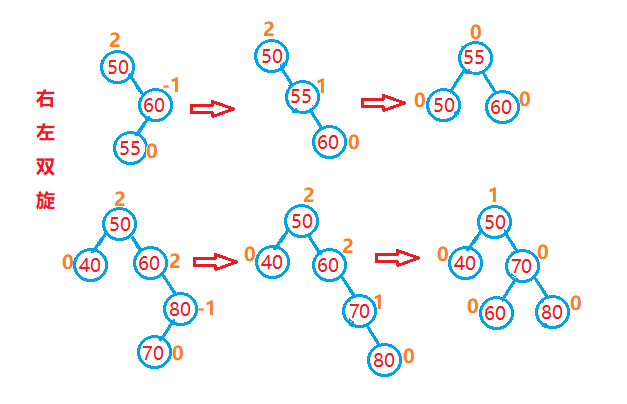
右左双旋:
当在较高右子树的左侧插入一个结点时,导致较高右子树的双亲结点失去平衡。此时是较高右子树的左侧导致的失衡,仅仅
依靠单旋已经没法调整平衡了。
判断是否为右左双旋的情况,如果是--->先使用右单旋,再使用左单旋。
具体实现
#include
using namespace std;
template
struct AVLTreeNode
{
AVLTreeNode()
{}
AVLTreeNode(T key, V value)
:_key(key)
, _value(value)
, _bf(0)
, _pLeft(NULL)
, _pRight(NULL)
, _pParent(NULL)
{}
T _key;
V _value;
int _bf;
AVLTreeNode* _pLeft;
AVLTreeNode* _pRight;
AVLTreeNode* _pParent;
};
template
class AVLTree
{
typedef AVLTreeNode Node;
typedef Node* PNode;
public:
AVLTree()
:_pRoot(NULL)
{}
void Insert(T key, V value)
{
_Insert(_pRoot, key, value);
}
void Delete(T key, V value)
{
_Delete(_pRoot, key, value);
}
void InOrder()
{
_InOrder(_pRoot);
}
bool Isbalance()
{
return _Isbalance(_pRoot);
}
private:
int GetHeight(PNode Root)
{
if (NULL == Root)
return 0;
int Left = GetHeight(Root->_pLeft);
int Right = GetHeight(Root->_pRight);
return (Left > Right) ? (Left + 1) : (Right + 1);
}
bool _Isbalance(PNode Root)
{
if (NULL == Root)
return true;
int LHeight = GetHeight(Root->_pLeft);
int RHeight = GetHeight(Root->_pRight);
int bf = RHeight - LHeight;
if (abs(bf) >= 2)
return false;
else
return _Isbalance(Root->_pLeft) && _Isbalance(Root->_pRight);
}
PNode Find(PNode& Root, T key, V value)
{
PNode pCur = Root;
while (pCur)
{
if (key < pCur->_key)
pCur = pCur->_pLeft;
else if (key > pCur->_key)
pCur = pCur->_pRight;
else
return pCur;
}
return NULL;
}
PNode FirstOfInOder(PNode& Root)
{
if (NULL == Root)
return NULL;
PNode pCur = Root;
while (pCur->_pLeft)
{
pCur = pCur->_pLeft;
}
return pCur;
}
void RotateL(PNode pParent)
{
PNode pSubR = pParent->_pRight;
PNode pSubRL = pSubR->_pLeft;
//更新pParent的右
pParent->_pRight = pSubRL;
if (pSubRL)
pSubRL->_pParent = pParent;
//更新PSubR的左和双亲
pSubR->_pLeft = pParent;
PNode parent = pParent->_pParent;
pSubR->_pParent = parent;
//更新pParent的双亲
//pParent为根
if (parent == NULL)
_pRoot = pSubR;
//pParent为双亲的左
else if (pParent == parent->_pLeft)
parent->_pLeft = pSubR;
//pParent为双亲的右
else if (pParent == parent->_pRight)
parent->_pRight = pSubR;
pParent->_pParent = pSubR;
pParent->_bf = 0;
pSubR->_bf = 0;
}
void RotateR(PNode pParent)
{
PNode pSubL = pParent->_pLeft;
PNode pSubLR = pSubL->_pRight;
//更新pParent的左
pParent->_pLeft = pSubLR;
if (pSubLR)
pSubLR->_pParent = pParent;
//更新pSubL的位置
PNode parent = pParent->_pParent;
pSubL->_pRight = pParent;
pSubL->_pParent = parent;
//更新pParent的双亲结点的指向
//pParent为根
if (NULL == parent)
_pRoot = pSubL;
//pParent为双亲结点的左孩子
else if (pParent == parent->_pLeft)
parent->_pLeft = pSubL;
//pParent为双亲结点的右孩子
else if (pParent == parent->_pRight)
parent->_pRight = pSubL;
pParent->_pParent = pSubL;
pParent->_bf = 0;
pSubL->_bf = 0;
}
void RotateLR(PNode pParent)
{
PNode pSubL = pParent->_pLeft;
PNode pSubLR = pSubL->_pRight;
int LR = pSubLR->_bf;
RotateL(pParent->_pLeft);
RotateR(pParent);
PNode parent = pParent->_pParent;
if (parent)
{
int left = GetHeight(parent->_pLeft);
int right = GetHeight(parent->_pRight);
parent->_bf = right - left;
}
if (LR == -1)
pParent->_bf = 1;
else if (LR == 1)
pSubL->_bf = -1;
}
void RotateRL(PNode pParent)
{
PNode pSubR = pParent->_pRight;
PNode pSubRL = pSubR->_pLeft;
int RL = pSubRL->_bf;
PNode parent = pParent->_pParent;
if (parent)
parent->_bf++;
RotateR(pParent->_pRight);
RotateL(pParent);
if (RL == 1)
pParent->_bf = -1;
else if (RL == -1)
pSubR->_bf = 1;
}
//旋转平衡调整
void _Rotate(PNode& pParent)
{
if(pParent)
{
if (pParent->_bf == -2)
{
if (pParent->_pLeft->_bf == -1)//较高左子树的左侧---右单旋
RotateR(pParent);
else if (pParent->_pLeft->_bf == 1)//较高左子树的右侧---左右双旋
RotateLR(pParent);
}
else if (pParent->_bf == 2)
{
if (pParent->_pRight->_bf == 1)//较高右子树的右侧---左单旋
RotateL(pParent);
else if (pParent->_pRight->_bf == -1)//较高右子树的左侧---右左双旋
RotateRL(pParent);
}
}
}
//调整平衡因子
void AdjustBf(PNode& pCur)
{
PNode pParent = pCur->_pParent;
while (pParent)
{
if (pCur == pParent->_pLeft)
pParent->_bf--;
else
pParent->_bf++;
if (0 == pParent->_bf)
break;
else if (1 == pParent->_bf || -1 == pParent->_bf)
{
pCur = pParent;
pParent = pCur->_pParent;
}
else
{
_Rotate(pParent);
break;
}
}
}
private:
void _InOrder(PNode& Root)
{
if (NULL == Root)
return;
_InOrder(Root->_pLeft);
cout << "<" << Root->_key << "," << Root->_value << ">" << endl;
_InOrder(Root->_pRight);
}
bool _Insert(PNode& Root, T key, V value)
{
if (NULL == Root)
{
Root = new Node(key, value);
return true;
}
PNode pCur = Root;
PNode pParent = NULL;
while (pCur)
{
if (key < pCur->_key)
{
pParent = pCur;
pCur = pCur->_pLeft;
}
else if (key > pCur->_key)
{
pParent = pCur;
pCur = pCur->_pRight;
}
else
return false;
}
pCur = new Node(key, value);
if (key < pParent->_key)
pParent->_pLeft = pCur;
else
pParent->_pRight = pCur;
pCur->_pParent = pParent;
AdjustBf(pCur);
return true;
}
private:
PNode _pRoot;
};
void TestAVLTre()
{
AVLTree avlt;
//int arr[] = { 11, 7, 18, 3 };
int arr[] = { 70, 50, 90, 30, 60,55};
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
avlt.Insert(arr[i], i);
}
avlt.InOrder();
//avlt.Insert(4, 4);
if (avlt.Isbalance())
cout << "this Tree is AVLTree" << endl;
else
cout << "this Tree is not AVLTree" << endl;
}