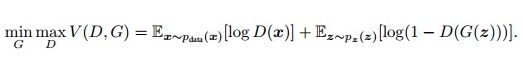PyTorch 学习笔记（十）：初识生成对抗网络（Generative Adversarial Networks，GANs）

2014年，深度学习三巨头之一Ian Goodfellow提出了生成对抗网络（Generative Adversarial Networks，GANs）这一概念，刚开始并没有引起轰动，直到2016年，学界、业界对它的兴趣如“井喷”一样爆发，多篇重磅文章陆续发表，Lecun这样形容GANs“adversarial training is the coolest thing since sliced bread”。2016年12月NIPS大会上，Goodfellow做了有关GANs的专题报告，使得GANs成为了当今最热门的研究领域之一，接下来具体介绍一下。

一. 何为对抗生成网络

生成对抗网络，根据它的名字，可以推断这个网络由两部分组成：第一部分是生成，第二部分是对抗。这个网络的第一部分是生成模型，就像之前自动编码器的解码部分；第二部分是对抗模型，严格来说它是一个判断真假图片的判别器。生成对抗网络最大的创新也是在此，这就是生成对抗网络与自动编码器最大的区别。简单来说，生成对抗网络就是让两个网络相互竞争，通过生成网络来生成假的数据，对抗网络通过判别器判别真伪，最后希望生成网络生成的数据能够以假乱真骗过判别器。

1. 生成模型

首先看看生成模型，笔记（九）里面已经给出了一般的生成模型。在生成对抗网络中，不再是将图片输入编码器得到隐含向量然后生成图片，而是随机初始化一个隐含向量，根据变分编码器的特点，初始化一个正态分布的隐含向量，通过类似解码的过程，将它映射到一个更高的维度，最后生成一个与输入数据相似的数据，这就是假的图片。这时自动编码器是通过对比两种图片每个像素点的差异计算损失函数的，而生成对抗网络会通过对抗过程来计算出这个损失函数。

2. 对抗模型

重点来介绍对抗过程，这个过程是生成对抗网络相对于之前的生成模型如自动编码器等最大的创新。

对抗过程简单来说就是一个判断真假的判别器，相当于一个二分类问题，输入一张真的图片希望判别器输出的结果是1，输入一张假的图片希望判别器输出的结果为0。这跟原图片的label没有关系，不管原图片到底是一个多少类别的图片，它们都统一称为真的图片，输出的label为1，则表示是真实的；而生成图片的label是0，则表示假的。

在训练过程中，先训练判别器，将假的数据和真的数据都输入给判别模型，这个时候优化这个判别模型，希望它能够正确地判断出真的数据和假的数据，这样就能够得到一个比较好的判别器。

然后开始训练生成器，希望它生成的假数据能够骗过现在这个比较好的判别器。具体做法就是将判别器的参数固定，通过反向传播优化生成器的参数，希望生成器得到的数据在经过判别器之后得到的结果能尽可能地接近1，这时只需要调整一下损失函数就可以了，之前在优化判别器的时候损失函数是让假的数据尽可能接近0，而现在训练生成器的损失函数是让假的数据尽可能接近1。

二. 生成对抗网络的数学原理

上一讲中已经提到过，KL divergence作为统计学中的一个基本概念，用于衡量两种分布概率的相似程度，数值越小，表示两种概率分布越接近。对于离散的概率分布，定义如下：
$D_{KL}(P||Q)={\sum }_{i}P(i)log\frac{P(i)}{Q(i)}$

对于连续的概率分布，定义如下：$D_{KL}(P||Q)={\int }_{-\infty }^{\infty }p(x)log\frac{p(x)}{q(x)}dx$

至于为什么可以用KL 散度来描述两种概率分布之间的接近程度，x为离散变量，考虑x的真实的未知分布为P(x)，我们可以从最优信息编码的角度来考虑，当对给定概率为P(x)的x分配一个$-logP(x)$的二进制位数进行编码，这样所需要的编码长度最小（因为按照这样的方式概率大的消息编码长度小，概率小的编码长度大），所以平均发送一个消息需要的编码长度为$-\sum P(x)logP(x)$，也即是分布$P(x)$包含的信息量的大小；假定现在用一个近似的分布Q(x)对它进行建模。，而由于使用了这个错误的分布$Q(x)$，所需要的平均编码长度增加了$-\sum P(x)logQ(x)-P(x)logP(x)=-\sum P(x)log\frac{Q(x)}{P(x)}$，也即是增加的信息量大小（编码长度越大，所蕴含的信息量越大）。

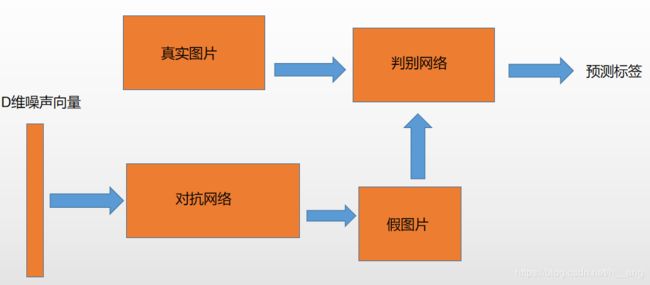
根据之前介绍的内容，要做的操作如下图：

如上图所示，想要一个高斯噪声$z$通过一个生成网络G得到一个和真实数据分布$p_{data}(x)$差不多的数据分布$p_G(x;\theta )$，其中参数$\theta$是网络的参数，其中参数$\theta$是生成网络的参数决定的，希望找到$\theta$使得$p_G(x;\theta )$和$p_{data}(x)$尽可能接近。

从真实数据分布$p_{data}(x)$中取样m个点，$\left\{x^1,x^2,x^3,...,x^m\right\}$，根据给定的参数$\theta$可以计算如下的概率$P_G(x^i;\theta )$，那么生成的m个样本数据的似然（likelihood）为：
$L={\prod }_{i=1}^m{P}_G(x^i;\theta )$

我们就是要找到${\theta }^{\ast }$来最大化似然估计：
${\theta }^{\ast }=argmax{\prod }_{i=1}^m{P}_G(x^i;\theta )\iff argmaxlog{\prod }_{i=1}^m{P}_G(x^i;\theta )=argmax{\sum }_{i=1}^{m}log{P}_G(x^i;\theta )$

我们现在让$x服从P_{data}$，那么${\theta }^{\ast }=argmax{E}_{x-P_{data}}[log{P}_G(x^i;\theta )]=argmax\sum P_{data}(x)log{P}_G(x;\theta )\iff argmax\sum P_{data}(x)log{P}_G(x;\theta )-argmax\sum P_{data}(x)log{P}_{data}(x)=argmax\sum P_{data}(x)log\frac{P_G(x;\theta )}{P_{data}(x)}=argmin\sum P_{data}(x)log\frac{P_{data}(x)}{P_G(x;\theta )}$

由此可以看出来，最小化KL散度等价于最大化似然函数。

Generator G是一个生成器，给定先验分布$P_{prior}(z)$，希望得到生成分布$P_G(x)$，这里很难通过极大似然估计得到结果。Discriminator D是一个函数，用来衡量$P_G(x)和P_{data}(x)$之间的差距，可用来取代极大似然估计。

首先，定义函数V(G,D)如下：

可以通过下面的式子求得最优的生成模型：

为什么定义了一个 V(G,D)然后通过求 max 和 min 就能够取得最优的生成模型呢？我们下面来定性分析一下。

前面说到过，网络的训练过程如下，循环k次更新判别器之后，使用较小的学习率来更新一次生成器的参数，将这个过程重复迭代几次：

可以看出来，我们定义的目标函数为 V(G,D)，当我们先训练判别器时，$P_G和P_{data}$固定，$argma{x}_{D}V(G,D)$的最大值对应的是“判别网络遇到真实数据输出 D(x)=1，遇到生成数据 D(x)=0”，这刚好也是我们希望判别网络达到的效果，也就说求V(G,D)得最大值对应着判别网络往更优的方向前进，换个角度来讲，训练时的损失函数也就可以看成是 - V(G,D)，即为上表中的$\frac{1}{m}{\sum }_{i=1}^m[logD(x^{(i)})+log(1-D(G(z^{(i)})))]$；之后训练生成网络时，$E_{x\sim P_{data}}[logD(x)]$是常量（损失函数可以不用考虑这部分），训练时我们希望生成的G(z)送入判别器中输出 D(x)=1，对应的是 V(G,D)的最小值，所以此时 $argminmaxV(G,D)$是正确的，也刚好契合了上表中的损失函数$\frac{1}{m}{\sum }_{i=1}^{m}log(1-D(G(z^{(i)}))$。

上面的分析是从 $argminmaxV(G,D)$开始的，我们说明了对V(G,D)求最大值对应的就是判别网络向更好的方向训练（即能正确区分真实数据与生成数据），然后再取最小值，对应的就是生成网络朝着我们期待的方向训练（即生成的输入送入前面训练好的判别网络时输出为1）。现在我们换个角度来推导下，仍然是从 $argminmaxV(G,D)$开始，来说明下通过这样的方法求得的G生成的数据分布和原数据分布最为接近。

首先我们只考虑$ma{x}_{D}V(G,D)$，在给定G的前提下，取一个合适的D使得V(G,D)能够取得最大值，这就是简单的微积分：
$V=E_{x\sim P_{data}}[logD(x)]+E_{x\sim P_G}[log(1-D(x))]={\int }_x{P}_{data}(x)logD(x)dx+{\int }_x{P}_G(x)log(1-D(x))dx={\int }_x[P_{data}(x)logD(x)+P_G(x)log(1-D(x))]dx$

对于这个微积分，要去它的最大值，希望对于给定的x，积分里面的项是最大的，也就是希望取到一个最优的$D^{\ast }$最大化这个$P_{data}(x)logD(x)+P_G(x)log(1-D(x))$式子。

在数据给定、G给定的前提下，$P_{data}(x)和P_G(x)$都可以看作是常数，分别用a和b表示它们，这样就可以得到如下的式子：
$f(D)=alog(D)+blog(1-D)$
$\frac{df(D)}{dD}=\frac{a}{D}-\frac{b}{1-D}=0$
$\iff a\times (1-D^{\ast })=b\times D^{\ast }$
$D^{\ast }(x)=\frac{a}{a+b}=\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}$

这样就求得了在给定G的前提下，能够使得V(D)取得最大值的D，将D带回原来的V(G,D)，得到如下的结果：
$maxV(G,D)=V(G,D^{\ast })=E_{x\sim P_{data}}[log\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}]+E_{x\sim P_G}[log\frac{P_G(x)}{P_{data}(x)+P_G(x)}]$
$={\int }_x{P}_{data}(x)log\frac{\frac{1}{2}{P}_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2}}dx+{\int }_x{P}_G(x)log\frac{\frac{1}{2}{P}_G(x)}{\frac{P_{data}(x)+P_G(x)}{2}}dx$
$=-2log2+KL(P_{data}(x)||\frac{P_{data}(x)+P_G(x)}{2})+KL(P_G(x)||\frac{P_{data}(x)+P_G(x)}{2})$
$=-2log2+2JSD(P_{data}(x)||P_G(x))$

这里引入了一个新概念，JS Divergence，定义如下：
$JSD(P||Q)=\frac{1}{2}[KL(P||M)+KL(Q||M)]，其中M=\frac{P+Q}{2}$

JSD散度相比较于KL散度，具备了对称性，且JS 散度的取值为 0 到 log2。若两个分布完全没有交集，那么 JS 散度取最大值 log2；若两个分布完全一样，那么 JS 散度取最小值 0，当且仅当 P=Q，即$P_{data}(x)=P_G(x)$时，JSD散度取最小值0，这也就是说通过 $argmi{n}_{G}V(G,D^{\ast })$求得的G会使得真实的数据分布和生成的数据分布差异性最小，这样自然可以生成一个和原分布尽可能接近的分布，同时也摆脱了计算极大似然估计，所以GAN的本质是通过改变训练的过程来避免繁琐的计算。相比较于VAE（变分自动编码器），GAN连度量都是用网络训练出来的，这比我们自己的平方误差损失函数要高明的多。

三. GAN的局限性

1. 在其他paper中提出，经过许多次训练，loss一直都是平的

JSD散度有一个严重的问题，如果两种分布之间完全没有重叠部分，或者说重叠部分可以忽略，那么JSD散度将恒等于常数log2.换句话说，就算两种分布很接近，但是只要它们没有重叠，那么JS Divergence就是一个常数，这就使得网络没有办法通过这个损失函数去学习，因为它没办法知道它是否做的好，进而导致梯度消失，同时这也使得我们没有办法衡量这两种分布到底有多靠近。

而真实分布与生成的分布没有重叠部分的概率有多大呢？其实是非常大的，直观来讲，真实分布是一个高维分布，而生成分布来自于一个低维分布，所以其实很有可能生成分布与真实分布之间就没有重叠的部分。除此之外，不可能真正去计算两个分布，只能近似采样，所以也导致了两个分布没有重叠部分。如果判别器训练得太好，那么生成分布和原来分布基本没有重叠部分，这就导致了梯度消失；如果判别器训练得不好，这样生成器得梯度又不准，就会出现错误得优化方向。如果要使得GAN能够完美的收敛，那么需要判别器训练的不好也不坏，而这个度是很难把握的，况且这还依赖数据的分布等条件，所以GAN才这麽难训练。

2. Model Collapse

GAN的优化目标是一个极小极大(minmax)问题，即 $\underset{G}{\min }\underset{D}{\max }V(G,D)$，也就是说，优化生成器的时候，最小化的是 $\underset{D}{\max }V(G,D)$。可是我们是迭代优化的，要保证V(G,D)最大化，就需要迭代非常多次，这就导致训练时间很长。如果我们只迭代一次判别器，然后迭代一次生成器，不断循环迭代。这样原先的极小极大问题，就容易变成极大极小(maxmin)问题，可二者是不一样的。如果变化为极大极小问题，那么迭代就是这样的，生成器先生成一些样本，然后判别器给出错误的判别结果并惩罚生成器，于是生成器调整生成的概率分布。可是这样往往导致生成器变“懒”，只生成一些简单的，重复的样本，即缺乏多样性，也叫mode collapse。

四. 代码

我发现生成器中BN层和ReLU的顺序很重要，在这里似乎ReLU+BN更好，而且训练时的问题很多，很容易就陷入loss一直是平的状态，这大概和上面谈到的局限性有关。

import torch
from torchvision import transforms, datasets
from torch import nn, optim
from torch.utils.data import DataLoader, sampler
from torch.autograd import Variable
import matplotlib.gridspec as gridspec

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['figure.figsize'] = (10.0, 8.0)
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# 超参数设置
batch_size = 100
NOISE_DIM = 96
NUM_TRAIN = 50000
NUM_VAL = 5000
def deprocess_img(x):
    return (x+1.0)/2.0

# 定义一个采样函数
class ChunkSampler(sampler.Sampler):
    """Samples elements sequentially from some offset.
    Arguments:
        num_samples: # of desired datapoints
        start: offset where we should start selecting from
    """
    def __init__(self, num_samples, start=0):
        self.num_samples = num_samples
        self.start = start

    def __iter__(self):
        return iter(range(self.start, self.start + self.num_samples))

    def __len__(self):
        return self.num_samples

def show_images(images):
    images = np.reshape(images, [images.shape[0], -1])
    sqrtn = int(np.ceil(np.sqrt(images.shape[0])))
    sqrtimg = int(np.ceil(np.sqrt(images.shape[1])))

    fig = plt.figure(figsize=(sqrtn, sqrtn))
    gs = gridspec.GridSpec(sqrtn, sqrtn)
    gs.update(wspace=0.05, hspace=0.05)

    for i, img in enumerate(images):
        ax = plt.subplot(gs[i])
        plt.axis('off')
        ax.set_xticklabels([])
        ax.set_yticklabels([])
        ax.set_aspect('equal')
        plt.imshow(img.reshape([sqrtimg, sqrtimg]))
    plt.show()
    return
data_tf = transforms.Compose([transforms.ToTensor(), transforms.Normalize([0.5], [0.5])])
train_set = datasets.MNIST('./mnist', train=True, download=True, transform=data_tf)
# 取MNIST训练集的前50000张作为train_data
train_data = DataLoader(train_set, batch_size=batch_size, sampler=ChunkSampler(NUM_TRAIN, 0))
val_set = datasets.MNIST('./mnist', train=True, download=True, transform=data_tf)
# 取MNIST训练集索引为50000-55000的5000张图片作为val_data
val_data = DataLoader(val_set, batch_size=batch_size, sampler=ChunkSampler(NUM_VAL, NUM_TRAIN))

imgs = deprocess_img(train_data.__iter__().next()[0].view(batch_size, 784)).numpy().squeeze()
show_images(imgs)

# 定义判别器
class discriminator(nn.Module):
    def __init__(self):
        super(discriminator, self).__init__()
        self.conv1 = nn.Sequential(                     # b, 1, 28, 28
            nn.Conv2d(1, 32, kernel_size=5, padding=2),   # b, 32, 28, 28
            nn.LeakyReLU(0.2, True),
            nn.AvgPool2d(2, 2)          # b, 32, 14, 14
        )
        self.conv2 = nn.Sequential(
            nn.Conv2d(32, 64, kernel_size=5, padding=2),  # b, 64, 14, 14
            nn.LeakyReLU(0.2, True),
            nn.AvgPool2d(2, 2)    # b, 64, 7, 7
        )
        self.fc = nn.Sequential(
            nn.Linear(64*7*7, 1024),
            nn.LeakyReLU(0.2, True),
            nn.Linear(1024, 1),
            nn.Sigmoid()   # 将输出映射到(0, 1)
        )
    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = x.view(x.size(0), -1)
        x = self.fc(x)
        return x

class generator(nn.Module):
    def __init__(self, noise_dim=NOISE_DIM):
        super(generator, self).__init__()
        self.fc = nn.Sequential(
            nn.Linear(noise_dim, 1024),
            nn.ReLU(True),
            nn.BatchNorm1d(1024),
            nn.Linear(1024, 7*7*128),
            nn.ReLU(True),
            nn.BatchNorm1d(7 * 7 * 128),
        )
        self.conv = nn.Sequential(
            nn.ConvTranspose2d(128, 64, kernel_size=4, stride=2, padding=1),   # b, 64, 14, 14
            nn.ReLU(True),
            nn.BatchNorm2d(64),
            nn.ConvTranspose2d(64, 1, 4, 2, padding=1),    # b, 1, 28, 28
            nn.Tanh()
        )
    def forward(self, x):
        x = self.fc(x)
        x = x.view(x.size(0), 128, 7, 7)
        x = self.conv(x)
        return x

bce_loss = nn.BCEWithLogitsLoss()

# 定义判别器的损失函数
def discriminator_loss(logits_real, logits_fake):
    size = logits_real.size(0)
    true_labels = Variable(torch.ones(size, 1).float().cuda())
    false_labels = Variable(torch.zeros(size, 1).float().cuda())
    loss = bce_loss(logits_real, true_labels) + bce_loss(logits_fake, false_labels)
    return loss

# 定义生成器的损失函数
def generator_loss(logits_fake):
    size = logits_fake.size(0)
    true_labels = Variable(torch.ones(size, 1).float().cuda())
    loss = bce_loss(logits_fake, true_labels)
    return loss

# 定义优化器
def get_optimizer(net):
    optimizer = optim.Adam(net.parameters(), lr=3e-4, betas=(0.5, 0.999))
    return optimizer

# 定义训练函数
def train_gan(D_net, G_net, D_optimizer, G_optimizer,
              show_every=250, noise_size=96, num_epochs=10):
    iter_count = 0
    for epoch in range(num_epochs):
        for x, _ in train_data:
            bs = x.size(0)
            # 判别网络
            real_data = Variable(x).cuda()
            logits_real = D_net(real_data)

            # 使用先验分布torch.rand()产生区间(0, 1)间的数据
            sample_noise = (torch.rand(bs, noise_size) - 0.5)/0.5   # ([-1, 1])
            g_fake_seed = Variable(sample_noise).cuda()
            # 生成假的数据
            fake_images = G_net(g_fake_seed)
            # 生成数据送入判别器的得分
            logits_fake = D_net(fake_images)
            # 判别器的误差函数
            discriminator_error = discriminator_loss(logits_real, logits_fake)
            D_optimizer.zero_grad()
            discriminator_error.backward()
            D_optimizer.step()

            # 使用生成网络产生新的数据
            sample_noise = (torch.rand(bs, noise_size) - 0.5)/0.5
            g_fake_seed = Variable(sample_noise).cuda()
            fake_images = G_net(g_fake_seed)
            logits_fake = D_net(fake_images)
            generator_error = generator_loss(logits_fake)
            G_optimizer.zero_grad()
            generator_error.backward()
            G_optimizer.step()

            if (iter_count % show_every == 0):
                print("epoch: {}, Iter: {}, D:{:.4}, G:{:.4}".format(epoch, iter_count, discriminator_error.data, generator_error.data))
                imgs_numpy = deprocess_img(fake_images.data.cpu().numpy())
                show_images(imgs_numpy)
                print("iter_count: {}".format(iter_count))
            iter_count += 1

# 开始训练
D_net = discriminator().cuda()
G_net = generator().cuda()

D_optimizer = get_optimizer(D_net)
G_optimizer = get_optimizer(G_net)

train_gan(D_net, G_net, D_optimizer, G_optimizer, num_epochs=20)

刚开始时，生成的数据如下：

训练20个epoch后，生成的数据如下：

参考

https://zhuanlan.zhihu.com/p/27295635
https://zhuanlan.zhihu.com/p/58812258
https://www.cnblogs.com/LXP-Never/p/9706790.html