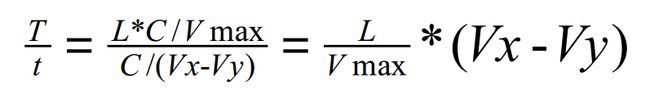暑假2019培训:Day3&Day4提高组测试赛
概述
因为前天暴了肝,导致昨天有些困,以至于没有写……
那么今天我来写Day3和Day4两天的题解吧~

题目顺序
Day3
- 1.三笔画
- 2.取石子
- 3.放积木
Day4
- 1.统计
- 2.绕圈跑
- 3.平衡集
Day3
1.三笔画(3lines)
【题目描述】
二维平面内有 n 个不同的点, Alice 需要在平面内画至多 3 条直线使得所有点在直线上。
问: Alice 能否完成任务, 如果能, 输出”YES”; 否则, 输出”NO”。
注意: 由于 Alice 的画图水平有限, 直线只能平行于坐标轴。
【输入数据】
第一行,一个整数 n。
接下来 n 行,第 i+1 行包含空格隔开的整数 xi,yi,表示第 i 个点的坐标。
【输出数据】
若 Alice 能完成任务, 输出”YES”, 否则输出”NO”。
【样例输入】
6
1 7
0 0
1 2
2 0
1 4
3 4
【样例输出】
YES
【样例解释】
三条直线分别为 x=1,y=0,y=4。
【数据范围】
对于 30%的数据,1 <= n <= 13。
对于 60%的数据,1 <= n <= 20。
对于 100%的数据,1 <= n <= 5e4,0 <= xi, yi <= 1e9。
做法
考虑这三条直线的状态,只可能为
(1)三条水平线
(2)两条水平线+一条垂直线
(剩余情况交换 x,y 坐标即可)
我们用一个数组统计同一 y 坐标上有几个点。
对于 1)的情况,只需判断是否只有三个及以下的 y 坐标上有点即可。
对于 2)的情况,可以枚举垂直线的 x 坐标,将这条垂直线上的点全部删去,判断剩下的
点的 y 坐标是否只有两种及以下。
将点按 x 坐标排序后即可做到 O(n)的扫描。
由于坐标较大,可以离散化预处理。
#include2.取石子(stone)
【题目描述】
有 n 堆石子,第 i 堆有 xi 个。
Alice 和 Bob 轮流取石子(先后手未定),Alice 每次从一堆中取走 a 个,Bob 每次从一
堆中取走 b 个,无法操作者输。
不难发现只会有四种情况:Alice 必胜;Bob 必胜;先手必胜;后手必胜。
你需要选定若干堆石子(共有 2^n 种方案),Alice 和 Bob 只能在你选出的堆中取,问
以上四种情况对应的方案数。对 10^9+7 取模。
【输入数据】
第一行三个整数 n,a,b,第二行 n 个整数 x1~xn。
【输出数据】
一行四个整数,分别表示 Alice 必胜、Bob 必胜、先手必胜和后手必胜的方案数,对
109+7 取模。
【样例输入】
2 2 3
2 3
【样例输出】
2 0 1 1
【样例解释】
选定空集时后手必胜, 选定{2}时 Alice 必胜, 选定{3}时先手必胜, 选定{2,3}时 Alice 必胜。
【数据范围】
对于 10%的数据,n, xi <= 5。
对于 50%的数据,n <= 20。
对于另外 10%的数据,a = b。
对于又另外 20%的数据,a = 1。
对于 100%的数据,1 <= n <= 1e5, 1 <= a, b, xi <= 1e9。
做法
假设a < b。
每堆石子先对a + b取模,然后可以分为4种:
(1)xi < a,没用。
(2)a <= xi < b,只要存在则a必胜。
(3)b <= xi < 2a,只和奇偶性有关。
(4)2a <= xi, 存在至少2个则a必胜, 存在1个且(3)为偶数则先手必胜, 存在1个且(3)为奇
数则a必胜, 不存在且(3)为奇数则先手必胜, 不存在且(3)为偶数则后手必胜。
时间复杂度 O(n)
#include3.放积木(block)
【问题描述】
Alice 有 n 块积木,放置第 i 块积木会占据区间[Li, Ri]。
Alice 每次会腾出一个区间放积木,她希望放的积木尽可能多,对每个询问区间,你需
要回答 Alice 最多可放置的积木数量。
注意: 积木与积木的放置区间不可重叠,且任意选定的积木放置区间不能超出询问区间。
【输入格式】
第一行三个整数 n,q,len,表示积木的数量,询问数和 len 的大小(数据保证 1≤Li,Ri≤
len)。
接下来 n 行,每行两个整数 Li,Ri,表示砖头的魔法标记。
接下来 q 行,每行两个整数 ai,bi,表示 moreD 选定的区间。
【输出格式】
对于每组询问输出对应的答案。
【输入样例】
3 2 4
1 2
2 3
3 4
1 3
3 3
【输出样例】
1
0
【数据范围】
对于 30%的数据满足 n <= 10, q <= 10。
对于 60%的数据满足 n <= 1,000, q <= 1,000, 1 <= Li, Ri <= 1,000。
对于 100%的数据满足 n <= 1e5, q <= 1e5, 1 <= Li, Ri <= len <= 1e5。
做法
对于 60%的数据,
我们可以用贪心算法。把所有线段按 Ri 小到大排序,每次询问时按 Ri 坐标从小到
大扫描所有线段,只要线段被区间包含且不与之前的线段冲突,那么就把这条线段加入
解。
时间复杂度 O(q*n)。
对于 100%的数据,
每次暴力扫描太慢了,考虑倍增。
f[i,j]表示从位置 i 开始,选择 2^j 条线段, Ri 最大的线段 Ri 最小是多少。显然所有
的 f[i,j]可以在 O(nlogn)的时间内计算出来(len 与 n 同级)。
询问时我们从 x 开始,从大到小枚举 k,如果选择 2^k 条线段后没有超出区间的范
围,那么答案加上 2^k,然后继续统计 f[x,k]+1~y 这段区间的答案。这样单次询问复杂
度是 O(logn)的,询问的总复杂度是 O(Qlogn),可以解决这道题。
60分:
#include
for(int i=1;i<=n;i++) if (a[i].y ^ a[i-1].y) b[a[i-1].y].y=i-1,b[a[i].y].x=i;
b[a[n].y].y=n;
// cout<<"------------------"<
// for(int i=1;i<=n;i++) cout<
// cout<<"------------------"<
for(int k=1;k<=m;k++) {
int l=read(),r=read();
int p=l,ans=0;
for(int i=l;i<=r;i++) if (a[b[i].x].x>=p) ans++,p=i+1;
printf("%d\n",ans);
}
return 0;
}
#include呼,昨天的任务终于完成了
Day4:
1.统计(statistic)
【 题目描述】
给定 n 个数,有 m 个询问。每次询问, Alice 想知道区间内[l, r]内是否出现过 xi 这个数。
【输入数据】
第一行一个整数 n。
第二行 n 个正整数 ai。
第三行一个整数 m。
接下来 m 行每行三个整数 li, ri 和 xi, 表示询问区间为[li, ri], 询问数字为 xi。
【输出数据】
对于每个询问,输出一个字符。 ‘0’表示没出现, ‘1’表示出现了。
【样例输入】
5
1234567 666666 3141593 666666 4343434
5
1 5 3141593
1 5 578202
2 4 666666
4 4 7135610
1 1 1234567
【样例输出】
10101
【数据说明】
对于 50%的数据, n <= 1000, m <= 1000。
对于 100%的数据, n <= 1e5, m <= 1e5, ai, xi <= 1e9。
做法
据说,这题是看昨天我们有没有认真听课的?
分块二分,模板题
成功满分(也是本场唯一一道我拿到超过10分的题)
当然也可以离线莫队 O(nsqrt(n)) 或直接开个桶用 set
但是莫队不优秀,常数太大,会被卡成50分的
#include2.绕圈跑(running)
【 题目描述】
n 个同学在长度为 C 的环形跑道上跑 L 圈。所有人的出发点相同,跑步的速度不同。
跑步过程中一个人可能会超过另一个人,即发生“套圈事件”。
Alice 想知道从开始跑步到第一名跑完全程的过程中,会发生多少次“套圈事件”。
注意: 由于不同学生的体能差异巨大, 一个人可能被另一个人套多圈。 (对于一对同学(x,y),
“套圈事件”的次数可能大于 1)。
【输入数据】
第一行三个整数: n, L 和 C。
第 2…n+1 行,每行一个整数。 第 i+1 行表示第 i 个同学的速度 vi。
【输出数据】
一个整数表示 “套圈事件”发生的总次数。
【样例输入】
4 2 100
20
100
70
1
【样例输出】
4
【样例解释】
4 个同学跑 2 圈,跑道长度为 100。
同学们的速度分别是: 20, 100, 70 和 1。
同学 2 花费 2 个单位时间跑完全程。
这段时间里发生了 4 次“套圈事件”: 同学 2 超过同学 1 和 4, 同学 3 超过同学 1 和 4。
【数据范围】
对于 30%的数据, n <= 5000
对于 100%的数据, n <= 1e5, 1 <= L, C <= 25000, 1 <= vi <= 1e6。
50%的数据 n <= 5000。
将所有人按速度排序,因为套圈事件只可能是速度快的人超过速度慢的人。
n ^ 2 枚举一对同学,计算它们发生的套圈事件次数。
设最快的人速度为 Vmax , 那么总用时 T = L * C / Vmax。
而一对同学(x, y) (Vx > Vy)发生一次套圈事件要 t = C / (Vx - Vy) 的时间。
所以一对同学(x, y)(Vx > Vy)对答案的贡献为:
考虑优化
L / Vmax 是个定值,我们只要求Σ(Vx - Vy)就可以了。
不过还没完,你会发现这么做样例都不过。
为什么?因为上面那个式子的答案要求是整除,而累加和之后答案自然会发生变化。
我们记录 L * Vx mod Vmax 的余数,计算整除后的答案, 再余数对答案的贡献记入
即可。 用 BIT 询问前缀和。
好,这是std……![]() (反正这题我爆零,暴力都不会打)
(反正这题我爆零,暴力都不会打)
#include 3.平衡集(subset)
【题目描述】
有 n 个正整数, 选出其中的若干个数构成一个非空可重集,若该可重集能被划分为和相
等的两个部分,则称它为平衡集。
问有多少个不同的平衡集。
平衡集 A,B 不同当且仅当存在下标为 i 的数在平衡集 A 中而不在平衡集 B 中。
【输入数据】
第一行输入 n,接下来 n 行每行输入一个正整数 ai。
【输出数据】
输出一共有多少种选法。
【样例输入】
4 1 2 3 4
【样例输出】
3
【 样例解释】
三个平衡集分别为{1, 2, 3}, {1, 3, 4}, {1, 2, 3, 4}。
【数据范围】
对于 20%的数据, n <= 10。
各有 5%的数据满足, n = 16, 17, 18, 19
对于 100%的数据, n <= 20, ai <= 1e8。
比较靠谱的暴力:
枚举一个集合,再枚举这个集合的子集,判断是否合乎题意。
复杂度为(3 ^ n),期望得分 30-40
n 太大了导致算法超时考虑将所有数分成两组(分别记作 Black 与 White)
若一个集合分成 A,B 两个子集后,他们的和相等即 Sum(A) = Sum(B)
就会有下面的等式出现:
Sum(Black in A) - Sum(Black in B) = Sum(White in B) - Sum(White in A)
对两组数分别处理:
将 Black 一组的所有可能分成的集合枚举出来,用 hash 记录 sum 差值,
对 White 组进行相同处理,若发现有某两个 sum 差值相等,则说明出现一个解。
复杂度大概为 O(6 ^ (n / 2) )
注意判重,同一种方案可能会出现多种不同的 sum 差值
#include