算法-分支限界法

（以下一些概念性的东西，抄袭网上的介绍！）

1、分支限界法

    (1)描述：采用广度优先产生状态空间树的结点，并使用剪枝函数的方法称为分枝限界法。

     所谓“分支”是采用广度优先的策略，依次生成扩展结点的所有分支（即：儿子结点）。
     所谓“限界”是在结点扩展过程中，计算结点的上界（或下界），边搜索边减掉搜索树的某些分支，从而提高搜索效率。

   (2)原理：按照广度优先的原则，一个活结点一旦成为扩展结点（E-结点）R后，算法将依次生成它的全部孩子结点，将那些导致不可行解或导致非最优解的儿子舍弃，其余儿子加入活结点表中。然后，从活结点表中取出一个结点作为当前扩展结点。重复上述结点扩展过程，直至找到问题的解或判定无解为止。

    (3)分支限界法与回溯法

     1)求解目标：回溯法的求解目标是找出解空间树中满足约束条件的所有解，而分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解。 
     2)搜索方式的不同：回溯法以深度优先的方式搜索解空间树，而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。

   (4)常见的分支限界法

    1)FIFO分支限界法(队列式分支限界法)

     基本思想：按照队列先进先出(FIFO)原则选取下一个活结点为扩展结点。

     搜索策略：一开始，根结点是唯一的活结点，根结点入队。从活结点队中取出根结点后，作为当前扩展结点。对当前扩展结点，先从左到右地产生它的所有儿子，用约束条件检查，把所有满足约束函数的儿子加入活结点队列中。再从活结点表中取出队首结点（队中最先进来的结点）为当前扩展结点，……，直到找到一个解或活结点队列为空为止。

    2)LC(least cost)分支限界法(优先队列式分支限界法)

    基本思想：为了加速搜索的进程，应采用有效地方式选择活结点进行扩展。按照优先队列中规定的优先级选取优先级最高的结点成为当前扩展结点。

    搜索策略：对每一活结点计算一个优先级（某些信息的函数值），并根据这些优先级；从当前活结点表中优先选择一个优先级最高（最有利）的结点作为扩展结点，使搜索朝着解空间树上有最优解的分支推进，以便尽快地找出一个最优解。再从活结点表中下一个优先级别最高的结点为当前扩展结点，……，直到找到一个解或活结点队列为空为止。

如果看完上边的介绍后，模拟两可，不妨根据以下几个例子，慢慢理解。（其实，之前也在不经意间用过很多次这个方法了。。。。）

例子1：0-1背包问题；

      //其实可以用动态规划很好的解决背包问题，但是这里用新的方法来解决；

有N件物品和一个容量为V的背包。第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。其中，每种物品只有一件，可以选择放或者不放。

n=3时，w={16,15,15}, c={45,25,25}, v=30

于是有：

注意：字母表示的是一种状态，A为根节点，B表示选择了物品w1的状态，C表示不选择物品w1的状态，D表示在含有物品1的情况下又选择了物品w2的状态，依此类推。时间复杂度是N^2;

两种方法：

    队列式分支限界法(处理法则:先进先出)：{}—>{A}—>{B,C}—>{C,D,E}(D是不可行解，舍弃)—>{C,E}—>{E,F,G}—>{F,G,J,K}(J是不可行解，舍弃)—>{F,G,K}—>{G,K,L,M}—>{K,L,M,N,O}—>{}

    优先队列式分支限界法(处理法则:价值大者优先)：{}—>{A}—>{B,C}—>{C，D，E}—>{C，E}—>{C，J，K}—>{C}—>{F，G}—>{G，L，M}—>{G，M}—>{G}—>{N，O}—>{O}—>{}

Java代码如下（包括先进先出原则和价值大者优先原则）

import java.util.Arrays;
import java.util.LinkedList;
import java.util.PriorityQueue;
import java.util.Queue;

import javax.management.Query;

//用分支界限算法来解决背包问题哈；
public class bagProblem1 {
	

	private int[] weight;
	private int[] value;
	private int sumV;
	
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		bagProblem1 bp = new bagProblem1();
		
		int[] w = {1,2,5,6,7};
		int[] c = {1,6,18,22,28};
		int sumV = 11;
		
		bp.weight = w;
		bp.value = c;
		bp.sumV = sumV;
	
		int maxValue;
		maxValue = bp.getMaxValueWithFifo();
		System.out.println(maxValue);
		
		maxValue = bp.getMaxValueWithPriority();
		System.out.println(maxValue);
	}
	
	//依据 价值大者优先 原则
	private int getMaxValueWithPriority() {
		// TODO Auto-generated method stub
		int maxValue = 0;
		PriorityQueue pq =  new PriorityQueue();
		pq.add(new status(0,0,-1));
		status st;
		int indextemp;
		while(pq.size()>0){
			st = pq.remove();
			indextemp = st.index +1;
			if(indextemp >= weight.length){
				continue;
			}
			if((st.currentW + weight[indextemp]) <= sumV){
				pq.add(new status(st.currentW + weight[indextemp],st.currenC + value[indextemp],indextemp));
				if(maxValue < st.currenC + value[indextemp]){
					maxValue = st.currenC + value[indextemp];
				}
			}

			pq.add(new status(st.currentW, st.currenC, indextemp));
		}
		return maxValue;
	}
		
//依据 先进先出的原则

	private int getMaxValueWithFifo() {
		int maxValue = 0;
		// TODO Auto-generated method stub
		LinkedList al = new LinkedList();
		al.add(new status(0,0,-1));
		
		status st;
		int indextemp;
		while(al.size()>0){
			st = al.remove();
			indextemp = st.index +1;
			
			if(indextemp >= weight.length){
				continue;
			}
			
			if((st.currentW + weight[indextemp]) <= sumV){
				al.add(new status(st.currentW + weight[indextemp],st.currenC + value[indextemp],indextemp));
				if(maxValue < st.currenC + value[indextemp]){
					maxValue = st.currenC + value[indextemp];
				}
			}
			al.add(new status(st.currentW, st.currenC, indextemp));
	
		}
		return maxValue;
	}
	
	//这个存放的总物品的价值和重量
	static class status implements Comparable{
		//当前的重量和价值；
		private int currentW;
		private int currenC;
		private int index;
		public status(int currentW,int currenC,int index){
			this.currentW = currentW;
			this.currenC = currenC;
			this.index = index;
		}
		@Override
		public int compareTo(status o) {
			// TODO Auto-generated method stub
			if(this.currentW > o.currentW){
				return 1;
			}
			if(this.currentW < o.currentW){
				return -1;
			}
			return 0;
		}
	}
}

例子2：单源加权最短路径问题

      在下图所给的有向图G中，每一边都有一个非负边权。要求图G的从源顶点s到目标顶点t之间的最短路径。

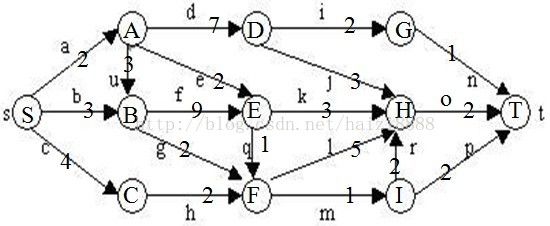
下图是用优先队列式分支限界法解有向图G的单源最短路径问题产生的解空间树。其中，每一个结点旁边的数字表示该结点所对应的当前路长。  

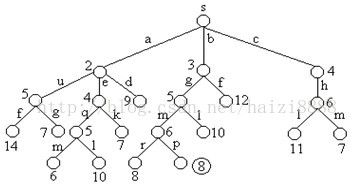
大致过程是这么个样子：广度遍历计算A,B,C节点路径信息，然后计算DEB，EF,F结点，因为有重复的节点，所以判断每次判断节点，如果当前节点的路径比存储的值小的话，那么我们将新的值覆盖原来的值，并且同时要判断队列中是否存在该节点，如果存在，那么删除该节点（避免重复计算，打个比方：比如有三个路径可以通向B节点，每次计算距离分别为2,3,4,5那么B节点被存储4次，这是比较影响效率的，所以要将含有B节点的给删除），出于效率考虑，我们每次从队列中取数，最好是取距离最短的数，因此，我们可以用TreeSet（二叉堆的实现原理）来存储数据；

Java代码如下：

 

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.TreeSet;
//为了方便将源点设为 J 目的节点设为K
public class shortestWithSigleSource {
	
	private ArrayList[] sourceal;
	private int[][] pathLen;
	private int[] finalpathLen;
	public shortestWithSigleSource(int vertCount){
		sourceal = new ArrayList[vertCount];
		pathLen = new int[vertCount][vertCount];
		for(int i=0;i();
		}
		
		sourceal[sourceint].add(desint);
		pathLen[sourceint][desint] = len;
	}
	
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		shortestWithSigleSource ma = new shortestWithSigleSource(11);
		//添加节点
		ma.addEdge('J', 'A',2);
		ma.addEdge('J', 'B',3);
		ma.addEdge('J', 'C',4);
		
		ma.addEdge('A', 'D',7);
		ma.addEdge('A', 'B',3);
		ma.addEdge('A', 'E',2);
		
		ma.addEdge('B', 'E',9);
		ma.addEdge('B', 'F',2);
		
		ma.addEdge('C', 'F',2);
		
		ma.addEdge('D', 'G',2);
		ma.addEdge('D', 'H',3);
		
		ma.addEdge('E', 'F',1);
		ma.addEdge('E', 'H',3);
		
		ma.addEdge('F', 'I',1);
		ma.addEdge('F', 'H',5);
		
		ma.addEdge('G', 'K',1);
		ma.addEdge('H', 'K',2);
		ma.addEdge('I', 'K',2);
		
		ma.getShortest();
		System.out.println(ma.finalpathLen['K'-'A']);
	}
	
	private void getShortest() {
		// TODO Auto-generated method stub
		TreeSet ts = new TreeSet();
		Node no = new Node('J'-'A',0);
		ts.add(no);
		finalpathLen['J'-'A'] = 0;
		
		Node verNode;
		int indextemp;
		while(ts.size() > 0){
			verNode = ts.pollFirst();
			if(sourceal[verNode.currentnode] == null){
				continue;
			}
			for(int i=0;i finalpathLen[verNode.currentnode] +pathLen[verNode.currentnode][indextemp]){
					ts.add(new Node(indextemp,finalpathLen[verNode.currentnode] +pathLen[verNode.currentnode][indextemp]));
					finalpathLen[indextemp] = finalpathLen[verNode.currentnode] +pathLen[verNode.currentnode][indextemp];
				}
			}
		}
	}

	
	static class Node implements Comparable{
		int currentnode;
		int pathLen ; 
		public Node(int currentnode,int pathLen){
			this.currentnode = currentnode;
			this.pathLen = pathLen;
		}
		@Override
		public int compareTo(Node o) {
			// TODO Auto-generated method stub
			if(this.pathLen > o.pathLen){
				return -1;
			}
			if(this.pathLen == o.pathLen){
				return 0;
			}
			return 1;
		}
	
	}

}