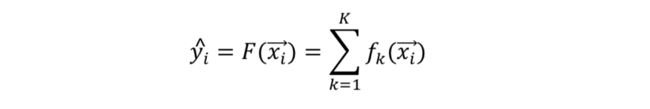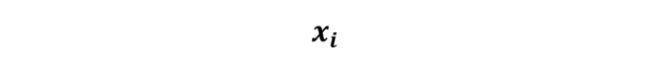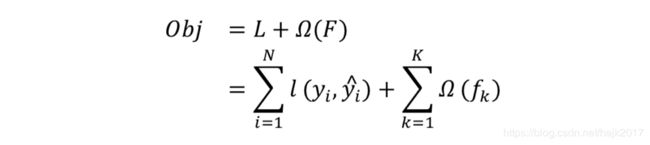慧安金科机器学习通识(三)| GBDT类算法原理简介
在插播了产品开发工程师的一些实战经验之后,我们回到机器学习的主线上来。上堂课讲到了决策树的一些基本概念和训练方法,本堂课我们介绍一下 GBDT 类算法的原理。
GBDT,英文全称为“Gradient Boost Decision Tree”,翻译为梯度提升树,这类算法是有监督业务的核心,主要包括 XGBoost、LightGBM 和 CatBoost等。
我们希望通过对这类算法原理的讲解,能够让更多的读者了解这类算法,更加灵活地将这类算法应用于实际业务当中,同时也希望可以借此减轻一些读者的数学恐惧症。
What is GBDT
梯度提升树(GBDT)可以分两部分来理解,一部分是梯度提升(Gradient Boosting),一部分是我们上堂课所讲的决策树(Decision Tree)。即:
GBDT = Gradient Boosting + Decision Tree
梯度提升又可以分为两部分,一部分是梯度下降(Gradient Descent),一部分是提升(Boosting)。即:
Gradient Boosting = Gradient Descent + Boosting
梯度下降是机器学习中的基本概念,在学习梯度下降之前,我们先来复习一下梯度(Gradient)这个重要概念。
Gradient and Gradient Descent
首先,我们回顾一下高数里学过的偏导数(Partial Derivative)。
偏导数
多变量函数表示具有多个变量的函数,例如:
f 相对于 x 的偏导数可以表示为(对 y 同理):
分别保持 x 和 y 不变(分别作为参量),我们可以得到 f 对 x 和对 y 的偏导数:
一个函数的梯度可以简单理解为一个函数对各个变量的偏导数组成的向量,一般表示如下:
例如对于上一小节中的函数:
我们可以得到:
一般地,
例如:
这个二元函数可以用一个山谷来表示:
在特定位置 ,按照负梯度的指示方向,下降得最快。
对于更多变量的函数,我们无法通过这种可视化的方式展现,他们像是高位空间中更抽象的“山谷”,但是负梯度总是能指示函数 f 的最大下降方向。
损失函数
假设我们有N个例子,那么:
常见的计算方式有平均绝对误差(MAE,Mean Absolute Error)和均方误差(MSE,Mean Squared Error):
那么,对应的公式为:
还有很多其他的计算方式,比如 Huber Loss:
Loss Function and Gradient Descent
然而,上节所述的负梯度仅指明了损失函数下降最快的方向,对于特定参数而言,在这个方向上调整多少,需要用学习率(Learning Rate)来控制。例如:
可以看出,学习率过小会让梯度下降的次数过多而消耗大量计算资源,学习率过大会直接跳过参数的最优解而让模型效果变差(极端情况下甚至会难以收敛而永远无法达到最优点),为了优化我们的函数,我们需要适当调整学习率。
在实践中,成功的模型训练并不意味着要找到“完美”(或接近完美)的学习效率,我们的目标是找到一个足够高的学习速率,该速率要能够使梯度下降过程高效收敛,但又不会高到使该过程永远无法收敛。
想象一个人在打高尔夫球,他每次挥杆都瞄向球洞,每次都会使球离球洞更近一些,如果挥杆的次数足够多,最后一定能把球打进球洞(图中蓝色抛物线为MSE损失函数)。
根据以上场景,我们可以用如下方式表示:
在这个打高尔夫球的场景里,我们只有一个例子(Example),因为我们只打了一次球;在真实数据集中,我们会有很多例子(粗浅的理解就是很多行数据),即会打很多次球,而打球的人就是我们的算法。
虽然理想情况下,数次挥杆后球能够进洞,但是对于不同情况(不同数据)我们无法知晓多少次挥杆才可以使球进洞(预测准确)。
所以,在实践中,我们通常会设置一个“挥杆次数”的上限,在代码参数中一般写作 n_estimators。
Gradient or Residual
先考虑一种特殊情况,当我们以作为损失函数的时候:
当我们舍去常数项 2/N 后,我们的损失函数的负梯度正是残差:
因为是一种非常常见的损失函数,而它作为损失函数的负梯度又刚好和残差相等,所以导致许多人把类算法中的负梯度和残差混为一谈,请注意这是严重的错误。
通常,机器学习的目标是最小化损失函数,所以我们通常采取梯度下降的方式。
但是我们有时可能会心生疑问,为什么不能直接使用残差呢?为了解释这个问题,我们先来看一个例子:
我们可以看出,损失函数很容易受到极端值的影响。
因此,为了保持模型的稳定,也不应直接使用残差作为我们的预测目标。
那梯度的优势在于哪里呢?我们以 Huber Loss 举例:
使用梯度:
使用残差:
可以看出,如果 δ 设置合适,采用梯度会比残差稳定得多。
Gradient Boosting and Decision Tree
回到上述打高尔夫球的例子,我们注意到整个打球的过程涉及到很多次挥杆,如果把这个打高尔夫球的人看成我们的最终集成模型,那他的每次挥杆都可以看作一次提升(Boosting),即:
每一次“挥杆”,即提升所用的训练模型可以称为基模型(Base model),那么对于模型整体而言,预测第 i 个例子时,可以用公式表示如下:
我们刚才假设了 F 包含了 K 个基模型,通常我们的基模型使用决策树,所以我们也常说 F 包含了 K 棵树。
在实际应用中,这里的 K 即 n_estimators,换言之 n_estimators = K。
注意数据中的单一例子包含不同的特征,因而我们把第 i 个例子写作向量(Vector)形式,即:
在其他文献中也常用加粗来表示向量,例如:
有时候在非正式场合也可以简单地写作:
既不加粗也不写作向量形式。
Objective Function
我们知道抑制过拟合(Overfitting)是机器学习模型的重大挑战,因而在训练 GBDT 模型的时候,我们既要考虑最小化损失函数 L,也要尽可能地降低模型的复杂度(Complexity)。
在此,我们用 Obj 来代表我们的目标函数,在实际操作中我们尝试最小化这个函数。
在数学上表示为:
“悟已往之不谏,知来者之可追”:我们的模型在做提升的时候都只考虑最优化当下的基模型。
用我们高尔夫球的例子直观理解就是每次打球都只能考虑球当下离球洞的位置和距离,之前打过的球已经没办法再后悔了。
所以我们每次只需做好当下的优化而不是总是考虑大局,那么在第次提升的时候,我们只需考虑:
那我们可以认为整个 GBDT 大模型的函数 Obj 也得到了优化。
Optimization of Objective Function
将变量包含在损失函数里相对来说还是不太好计算,尤其是对于比较复杂的损失函数,因此,我们采用泰勒展开(Taylor Expansion)来优化我们的损失函数
泰勒展开公式:
定义:
注意,如果我们只保留泰勒展开的一次导项,那就是前文所述经典的梯度下降;保留二次导项是 XGBoost 所采用的方式,从广义上讲,这也是梯度下降方法的一种。
Calculate the Weight of Leaves
在我们的模型中,我们主要是需要预测具体的值,所以实际上我们使用的是回归树(Regression Tree)。
假设我们的决策树有 T 片叶子,叶子权重(leaf weight)是我们赋予这片叶子的预测值。
对于我们第棵决策树的复杂度,我们采用如下定义(其中 γ 和 λ 是参数):
因为一个叶子有多个例子,我们针对叶子进行如下定义:
如果我们固定树的结构,那现在对于目标函数的变量只有我们还没具体赋值的权重。
此时为了最小化目标函数,我们令其一阶导数为零,可以解得:
代入目标函数可得:
How to Divide the Decision Tree
回顾我们之前学过的决策树算法,在每一次分裂(split)出新叶片之前,我们都会用 Gini 系数或者信息熵的收益(gain)来判断分裂该节点时是否值得;而对于 GBDT 算法而言,我们则着重考虑目标函数。
考虑到我们在某处分裂出节点一左一右,分别用 L 和 R 来表示
分裂前的目标函数是:
分裂后的目标函数是:
对于这次的收益则是两式相减:
Conclusions
References
-
Google Developers. Google Machine Learning Crash Course. Google LLC, 2019.
-
Cheng Li. A Gentle Introduction to Gradient Boosting. College of Computer and Information Science, Northwestern University, 2019.
-
Tianqi Chen. Introduction to Boosted Trees. Paul G. Allen School of Computer Science & Engineering, University of Washington, 2019.
-
Evan Xiong. Understanding GBDT Principles in One Text, 2018.
-
Yxd. In Depth Analysis of GBDT Principles, 2016.
-
Prince Grover. Gradient Boosting from Scratch, 2017.
-
Ben Gorman. Gradient Boosting Explained, 2017.
-
Terence Parr, Jeremy Howard. How to Explain Gradient Boosting, 2019.
-
Alexey Natekin, Alois Knoll. Gradient Boosting Machines, a Tutorial, 2013.
想了解有关机器学习的更多内容,请关注“慧安金科机器学习通识”系列文章。
下期预告:CNN、GNN
相关文章:
慧安金科机器学习通识(一)
慧安金科机器学习通识(二)|决策树的基本概念和训练方法
成为大数据工程师需要哪些技能?(一文秒懂大数据)
什么是KNN算法?
机器学习的“进化”
什么是机器学习?(上)
什么是机器学习?(下)