机器学习之支持向量机（Support Vector Machines）模型
机器学习之支持向量机模型
- 1、支持向量机模型介绍
- 2、支持向量机数学原理
- 3、算法及Python
- 4、小结
1、支持向量机模型介绍
支持向量机（SVM）是一种二类分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；支持向量机还包括核技巧，这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，支持向量机的学习算法是求解凸二次规划的最优算法。
定义一（线性可分支持向量机）：
给定线性可分训练数据集，通过间隔最大化或等价地求解相应的凸二次规划问题学习得到的分离超平面为
以及相应的分类决策函数
称为线性可分支持向量机。
>
定义二（非线性支持向量机）：
从非线性分类训练集，通过核函数与软间隔最优化，或凸二次规划，学习得到的分类决策函数
f(x)=sign(∑i=1Na∗iyiK(x,xi)+b∗) f ( x ) = s i g n ( ∑ i = 1 N a i ∗ y i K ( x , x i ) + b ∗ )
称为非线性支持向量机，K(x,z)是正定核函数。
>
2、支持向量机数学原理
函数间隔：对于给定的训练数据集和超平面(w,b)，定义超平面(w,b)关于样本点( xi,yi x i , y i )的函数间隔为
几何间隔：对于给定的训练数据集和超平面(w,b)，定义超平面(w,b)关于样本点( xi,yi x i , y i )的几何间隔为
间隔最大化
maxw,bγ m a x w , b γ
s.t. yi(w||w||⋅xi+b||w||)≥γ, i=1,2,⋯,N s . t . y i ( w | | w | | ⋅ x i + b | | w | | ) ≥ γ , i = 1 , 2 , ⋯ , N
即希望最大化超平面(w,b)关于训练集的几何间隔 γ γ ，约束条件表示是超平面(w,b)关于每个训练样本点的几何间隔至少是 γ γ .
可以将问题改写为
maxw,bγ^||w|| m a x w , b γ ^ | | w | |
s.t. yi(w⋅xi+b)≥γ^, i=1,2,⋯,N s . t . y i ( w ⋅ x i + b ) ≥ γ ^ , i = 1 , 2 , ⋯ , N
因为假设将 w⋅x+b=0 w ⋅ x + b = 0 中左边乘以 λ λ 则对于超平面没有影响，但是对样本点的函数间隔却有影响，因此我们可以通过调整 λ λ 值使 γ^=1 γ ^ = 1 此时便得到线性可分支持向量机学习的最优化问题
软间隔最大化：
当数据集中有一些特异点时，可能导致数据集线性不可分，此时可以对每个样本点 (xi,yi) ( x i , y i ) 引入一个松弛变量 ξi≥0, ξ i ≥ 0 , 使函数间隔加上松弛变量大于等于1，这样约束条件变为
同时对每个松弛变量支付一个代价 ξi ξ i ，目标函数由原来的 12||w||2 1 2 | | w | | 2 变为
12||w||2+C∑i=1Nξi 1 2 | | w | | 2 + C ∑ i = 1 N ξ i
这里，C>0称为惩罚参数，一般由应用问题决定
线性不可分的线性支持向量机的学习问题变为如下凸二次规划问题（原始问题）
minw,bξ 12||w||2+C∑i=1Nξi m i n w , b ξ 1 2 | | w | | 2 + C ∑ i = 1 N ξ i
学习的对偶算法：
应用拉格朗日对偶性，通过求解对偶问题得到原始问题的最优解，这样做的优点是，一是对偶问题往往更容易求解；二是自然引入核函数，进而推广到非线性分类问题。
线性可分支持向量机对偶问题
首先构建拉格朗日函数，为此，对每一个不等式约束引进拉格朗日乘子 αi≥0，i=1,2,⋯,N α i ≥ 0 ， i = 1 , 2 , ⋯ , N 定义拉格朗日函数
L(w,b,α)=12||w||2−∑i=1Nαiyi(w⋅xi+b)+∑i=1Nαi L ( w , b , α ) = 1 2 | | w | | 2 − ∑ i = 1 N α i y i ( w ⋅ x i + b ) + ∑ i = 1 N α i
其中， α=(α1,α2,⋯,αN)T α = ( α 1 , α 2 , ⋯ , α N ) T 为拉格朗日乘子向量。
根据拉格朗日对偶性，可得到对偶最优化问题
mina 12∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi m i n a 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i
s.t. ∑i=1Nαiyi=0 s . t . ∑ i = 1 N α i y i = 0
线性不可分线性支持向量机对偶问题
maxa −12∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)+∑i=1Nαi m a x a − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i
s.t. ∑i=1Nαiyi=0 s . t . ∑ i = 1 N α i y i = 0
非线性支持向量机最优化问题对偶问题
mina 12∑i=1N∑j=1NαiαjyiyjK(xi,xj)−∑i=1Nαi m i n a 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i
s.t. ∑i=1Nαiyi=0 s . t . ∑ i = 1 N α i y i = 0
3、算法及Python实现
线性支持向量机学习算法
输入：训练数据集 T=(x1,y1),(x2,y2),⋯,(xN,xN) T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , x N ) ,其中， xi∈χ=Rn,y∈Υ={−1,+1}，i=1,2,⋯,N; x i ∈ χ = R n , y ∈ Υ = { − 1 , + 1 } ， i = 1 , 2 , ⋯ , N ;
输出：分离超平面和分类决策函数。
（1）选择惩罚参数C>0，构造并求解凸二次规划问题
mina 12∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi m i n a 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i
s.t. ∑i=1Nαiyi=0 s . t . ∑ i = 1 N α i y i = 0
0≤αi≤C, i=1,2,⋯,N 0 ≤ α i ≤ C , i = 1 , 2 , ⋯ , N
求得最优解 α∗=(α∗1,α∗2,⋯,α∗N)T α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T
（2）计算 w∗=∑Ni=1α∗iyixi w ∗ = ∑ i = 1 N α i ∗ y i x i
选择 α∗ α ∗ 的一个分量 α∗j α j ∗ 适合条件0< α∗j<C α j ∗ < C 计算
b∗=yj−∑i=1Nyiα∗i(xi⋅xj) b ∗ = y j − ∑ i = 1 N y i α i ∗ ( x i ⋅ x j )
（3）求得分离超平面
w∗⋅x+b∗=0 w ∗ ⋅ x + b ∗ = 0
分类决策函数：
f(x)=sign(w∗⋅x+b∗) f ( x ) = s i g n ( w ∗ ⋅ x + b ∗ )
非线性支持向量机学习算法
输入：训练数据集 T=(x1,y1),(x2,y2),⋯,(xN,xN) T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , x N ) ,其中， xi∈χ=Rn,y∈Υ={−1,+1}，i=1,2,⋯,N; x i ∈ χ = R n , y ∈ Υ = { − 1 , + 1 } ， i = 1 , 2 , ⋯ , N ;
输出：分类决策函数。
1）选择适当的核函数K(x,z)和适当的参数C，构造并求解最优化问题
mina 12∑i=1N∑j=1NαiαjyiyjK(xi,xj)−∑i=1Nαi m i n a 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i
s.t. ∑i=1Nαiyi=0 s . t . ∑ i = 1 N α i y i = 0
0≤αi≤C, i=1,2,⋯,N 0 ≤ α i ≤ C , i = 1 , 2 , ⋯ , N
求得最优解 α∗=(α∗1,α∗2,⋯,α∗N)T α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T
（2）选择 α∗ α ∗ 的一个正分量0< α∗j<C α j ∗ < C 计算
b∗=yj−∑i=1Nα∗iyiK(xi⋅xj) b ∗ = y j − ∑ i = 1 N α i ∗ y i K ( x i ⋅ x j )
（3）构造决策函数
w∗⋅x+b∗=0 w ∗ ⋅ x + b ∗ = 0
分类决策函数：
f(x)=sign(∑i=1Nα∗iyiK(x⋅xi)+b∗) f ( x ) = s i g n ( ∑ i = 1 N α i ∗ y i K ( x ⋅ x i ) + b ∗ )
当K(x,z)是正定核函数时，上述问题是凸二次规划问题，解是存在的。
为了更为高效的求解凸二次规划问题，这里介绍由Platt于1998年提出的序列最小最优化（SMO）算法。
SMO算法
输入：输入：训练数据集 T=(x1,y1),(x2,y2),⋯,(xN,xN) T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , x N ) ,其中， xi∈χ=Rn,y∈Υ={−1,+1}，i=1,2,⋯,N，精度ε; x i ∈ χ = R n , y ∈ Υ = { − 1 , + 1 } ， i = 1 , 2 , ⋯ , N ， 精 度 ε ;
输出：近似解 α^ α ^ .
（1）取初值 α(0)=0 α ( 0 ) = 0 ，令k=0；
（2）选取最优化变量 α(k)1,α(k)1 α 1 ( k ) , α 1 ( k ) 解析求解两个变量的最优化问题，求得最优解 α(k+1)1,α(k+2)1 α 1 ( k + 1 ) , α 1 ( k + 2 ) ，更新 α为α(k+1) α 为 α ( k + 1 )
（3）若在精度 ε ε 范围内满足停止条件
∑i=1Nαiyi=0 ∑ i = 1 N α i y i = 0
0≤αi≤C, i=1,2,⋯,N 0 ≤ α i ≤ C , i = 1 , 2 , ⋯ , N
yi⋅g(xi)=⎧⎩⎨≥1,=1,≤1,{xi|αi=0}{xi|0<αi<C}{xi|αi=C} y i ⋅ g ( x i ) = { ≥ 1 , { x i | α i = 0 } = 1 , { x i | 0 < α i < C } ≤ 1 , { x i | α i = C }
其中，
g(xi)=∑j=1KαjyjK(xj,xi)+b g ( x i ) = ∑ j = 1 K α j y j K ( x j , x i ) + b
则转（4）；否则令k=k+1，转（2）；
（4）取 α^=α(k+1) α ^ = α ( k + 1 ) 。
Python代码实现
SMO算法求解线性可分支持向量机代码
from numpy import *
def loadDataSet(fileName):
dataMat = [];labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]),float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
def selectJrand(i,m):
j = i
while(j==i):
j = int(random.uniform(0,m))
return j
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def smoSimple(dataMatIn,classLabels,C,toler,maxIter):
dataMatrix = mat(dataMatIn);labelMat = mat(classLabels).transpose()
b = 0; m,n = shape(dataMatrix)
alphas = mat(zeros((m,1)))
iter = 0
while(iter0
for i in range(m):
fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T))+b
Ei = fXi - float(labelMat[i])
if ((labelMat[i]*Ei < - toler) and (alphas[i]or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i,m)
fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T))+b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy()
alphaJold = alphas[j].copy()
if(labelMat[i] != labelMat[j]):
L = max(0,alphas[j]-alphas[i])
H = min(C,C+alphas[j] - alphas[i])
else:
L = max(0,alphas[j]+alphas[i]-C)
H = min(C,alphas[j]+alphas[i])
if L==H:
# print("L==H");
continue
eta = 2.0*dataMatrix[i,:]*dataMatrix[j,:].T-dataMatrix[i,:]*dataMatrix[i,:].T-dataMatrix[j,:]*dataMatrix[j,:].T
if eta >=0:
# print("eta>=0");
continue
alphas[j] -= labelMat[j] *(Ei - Ej)/eta
alphas[j] = clipAlpha(alphas[j],H,L)
if(abs(alphas[j]-alphaJold) < 0.000001):
# print("j not moving enough");
continue
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold-alphas[j])
b1 = b - Ei -labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*\
dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej - labelMat[i]*(alphas[i]-alphaIold)*labelMat[j]*alphas[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]): b = b1
elif (0and (C > alphas[j]): b = b2
else: b = (b1+b2)/2.0
alphaPairsChanged += 1
# print("iter:%d i:%d,pairs changed %d "%(iter,i,alphaPairsChanged))
if(alphaPairsChanged == 0): iter += 1
else: iter = 0
# print("iteration number: %d"% iter)
return b,alphas
def calcWs(alphas,dataArr,classLabels):
X = mat(dataArr); labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
def plotData(dataArr,labelArr,ws,b):
import matplotlib.pyplot as plt
fig = plt.figure()
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
xPlotx,xPloty,oPlotx,oPloty = [],[],[],[]
for i in range(len(labelArr)):
label = labelArr[i]
if label == 1:
xPlotx.append(dataArr[i][0])
xPloty.append(dataArr[i][1])
elif label == -1:
oPlotx.append(dataArr[i][0])
oPloty.append(dataArr[i][1])
plt.title("SVM")
pPlot1,pPlot2 = plt.plot(xPlotx,xPloty,'bx',oPlotx,oPloty,'ro')
#Plot the split line
w0 = ws[0][0]
w1 = ws[1][0]
x = linspace(1,8,100)
y = -(w0/w1)*x-b[0][0]/w1
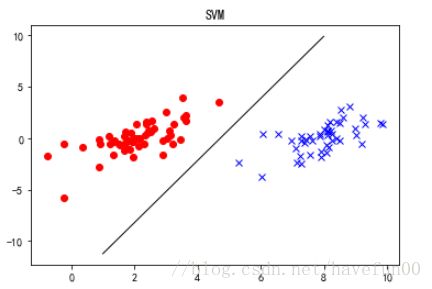
pSplitPlot = plt.plot(x,y,'k',lw=1)
plt.show() 绘制线性可分支持向量机超平面，所用的数据集SVM.rar
dataArr,labelArr = loadDataSet('./SVM/testSet.txt')
# print(labelArr)
b,alphas = smoSimple(dataArr,labelArr,0.6,0.001,40)
ws = calcWs(alphas,dataArr,labelArr)
b = array(b)
plotData(dataArr,labelArr,ws,b)绘制的图形如下
4、小结
支持向量机是一种分类器，称为“机”是因为它会产生一个二值决策结果，即决策“机”。支持向量机的泛化错误率较低，具有良好的学习能力，且学到的结果具有很好的推广性，这些优点使得支持向量机十分流行。John Platt引入了SMO算法，此算法可以通过每次优化两个alpha值来加快SVM的训练速度。
核方法或者说核技巧会将数据（有时是非线性数据），从一个低维空间映射到一个高维空间，可以将一个在低维空间中的非线性问题转换为高维空间下的线性问题来求解，核方法不仅在SVM中适用，还可以用于其他算法中。而其中的径向基函数是一个常用的度量两个方向距离的核函数。
常用的核函数
1、多项式核函数(polynomial kernel function)
K(x,z)=(x⋅z+1)p K ( x , z ) = ( x ⋅ z + 1 ) p
2、高斯核函数（Gaussian kernel function）
K(x,z)=exp(−||x−z||22σ2) K ( x , z ) = e x p ( − | | x − z | | 2 2 σ 2 )
3、字符串核函数（string kernel function）