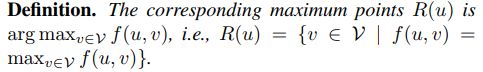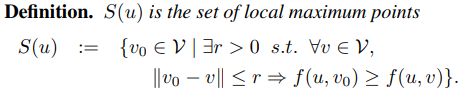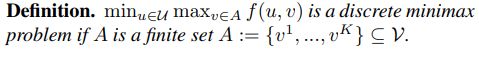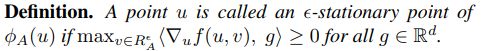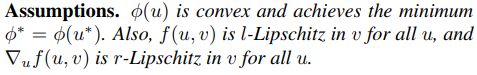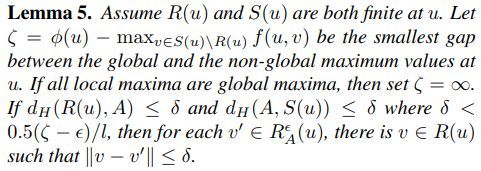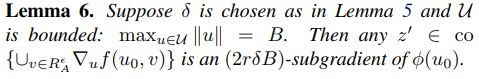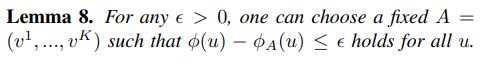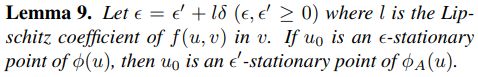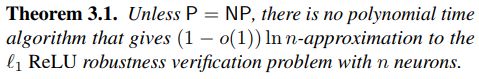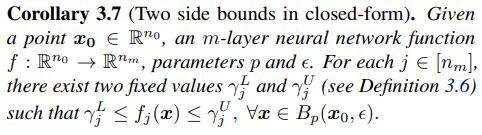ICML 2018 深度学习论文及代码集锦(8)
[1] Geometry Score: A Method For Comparing Generative Adversarial Networks
Valentin Khrulkov, Ivan Oseledets
Skolkovo Institute of Science and Technology, Institute of Numerical Mathematics RAS
http://proceedings.mlr.press/v80/khrulkov18a/khrulkov18a.pdf
下面是原始数据和GAN生成的数据对比如下
计算RLT的算法伪代码如下
其中RLT为relative living times。
计算几何相似度的算法伪代码如下
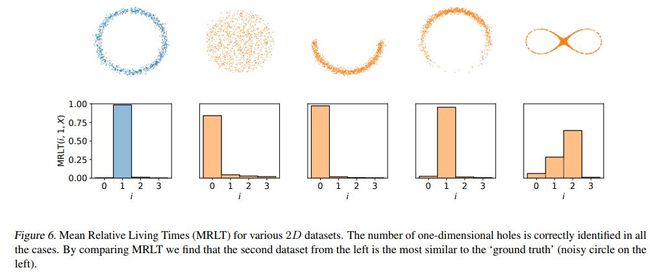
不同数据集的平均RLT对比如下
不同方法的几何得分对比如下
代码地址
https://github.com/KhrulkovV/geometry-score
https://github.com/igul222/improved_wgan_training
https://github.com/carpedm20/DCGAN-tensorflow
https://github.com/hep-lbdl/CaloGAN
[2] K-Beam Minimax: Efficient Optimization for Deep Adversarial Learning
Jihun Hamm, Yung-Kyun Noh
The Ohio State University, Seoul National University
http://proceedings.mlr.press/v80/hamm18a/hamm18a.pdf
定义一
![]()
定义二
定义三
定义四
定义五
引理一
定义六
引理二
K-beam -subgradient descent 算法伪代码如下
梯度方向算法如下
假设
引理三
引理四
引理五
引理六
定理七
引理八
引理九
代码地址
https://github.com/jihunhamm/k-beam-minimax
[3] Learning Dynamics of Linear Denoising Autoencoders
Arnu Pretorius, Steve Kroon, Herman Kamper
Stellenbosch University, CSIR/SU Centre for Artificial Intelligence Research
http://proceedings.mlr.press/v80/pretorius18a/pretorius18a.pdf
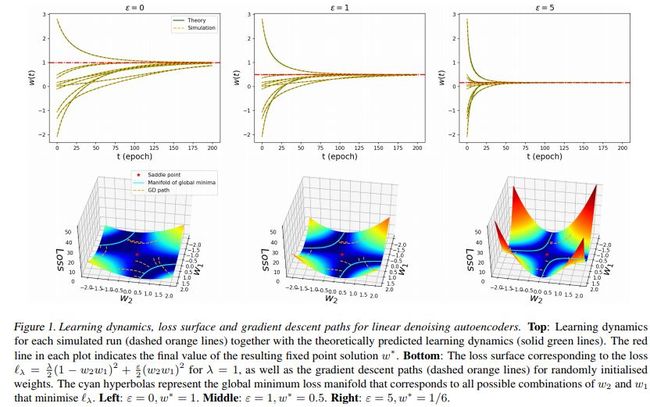
不同参数对模型的影响如下
代码地址
https://github.com/arnupretorius/lindaedynamics_icml2018
[4] Towards Fast Computation of Certified Robustness for ReLU Networks
Tsui-Wei Weng, Huan Zhang, Hongge Chen, Zhao Song, Cho-Jui Hsieh, Duane Boning, Inderjit S. Dhillon, Luca Daniel
Massachusetts Institute of Technology, UC Davis, Harvard University, UT Austin
http://proceedings.mlr.press/v80/weng18a/weng18a.pdf
定理3.1
推论3.2
定义3.3
定义3.4
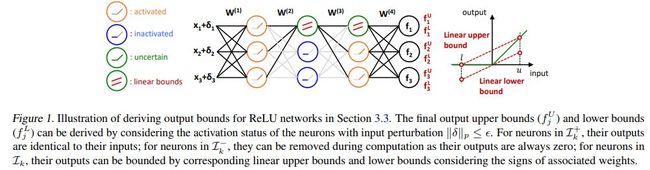
本文网络结构如下
定理3.5
定义3.6
推论3.7
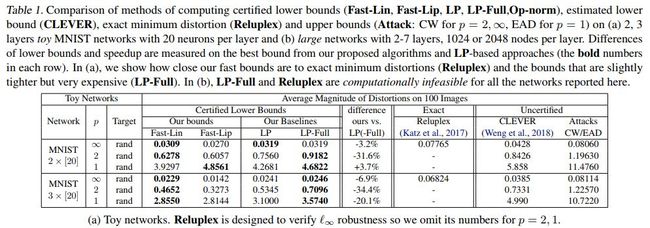
不同方法结果对比如下
代码地址
https://github.com/huanzhang12/CertifiedReLURobustness
[5] prDeep: Robust Phase Retrieval with a Flexible Deep Network
Christopher A. Metzler, Philip Schniter, Ashok Veeraraghavan, Richard G. Baraniuk
Rice University, The Ohio State University
http://proceedings.mlr.press/v80/metzler18a/metzler18a.pdf
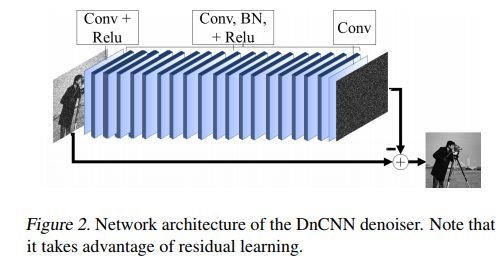
dnCNN网络结构如下
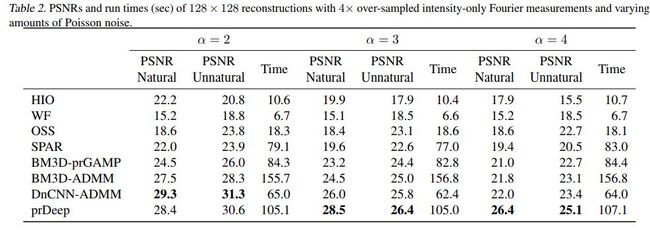
多种方法的效果对比如下
代码地址
https://github.com/ricedsp/prDeep
您可能感兴趣