强化学习经典算法笔记(三)：蒙特卡罗方法Monte Calo Method

强化学习经典算法笔记——蒙特卡罗方法

强化学习经典算法笔记(零)：贝尔曼方程的推导
强化学习经典算法笔记(一)：价值迭代算法Value Iteration
强化学习经典算法笔记(二)：策略迭代算法Policy Iteration

  前三篇都是在环境模型已知的情况下求解最优算法，但是很多情况下，环境的模型是未知的，我们不清楚状态之间如何转移，回报的概率是多少，甚至不清楚全部的状态空间长什么样子。这种情况下，如果不采用model-based方法（即，对复杂环境进行建模，建模过程其实就是学习过程，模型建的充分了，智能体对环境就理解充分了，就可以得出最优policy），而是采用model-free的方法（不去对环境进行建模，只用采样的方式学习出一个最优policy），最经典的就是蒙特卡罗算法了。

蒙特卡罗方法

  蒙特卡罗的思想早已有之。谈及Monte Calo，必说布丰投针实验。我们做一个改进实验：一个正方形区域边长为$a$，其中均匀分布了$N$个散点，取定正方形左下角是原点$O$，计算每个点与原点的距离$l$，统计$l\le a$的点数量为$M$，则
$$\frac{\frac{1}{4}\pi a^2}{a^2}=\frac{M}{N}$$
即$\pi =4M/N$。生成均匀分布的散点，即可以看做分别在四分之一圆和正方形的面积中采样，只要点数够多，散点的数量之比就能代表面积之比。这其中就蕴含着Monte Calo的核心思想——采样Sampling，通过充足的采样来模拟真实环境。

  下面是简单代码。

import numpy as np
import math
import random
import matplotlib.pyplot as plt
%matplotlib inline

square_size = 1

# 圆内点数
points_inside_circle = 0

# 方形点数
points_inside_square = 0

# 散点数量
sample_size = 2000

# 用于画圆曲线，计算时不用
arc = np.linspace(0, np.pi/2, 100)

def generate_points(size):
    # 生成散点
    x = random.random()*size
    y = random.random()*size
    return (x, y)

def is_in_circle(point, size):
    # 判断散点是否在圆内，欧氏距离
    return math.sqrt(point[0]**2 + point[1]**2) <= size

def compute_pi(points_inside_circle, points_inside_square):
    # 计算 4*M/N
    return 4 * (points_inside_circle / points_inside_square) 

plt.axes().set_aspect('equal')
plt.plot(1*np.cos(arc), 1*np.sin(arc))

for i in range(sample_size):
    point = generate_points(square_size)
    plt.plot(point[0], point[1], 'c.')
    points_inside_square += 1
    if is_in_circle(point, square_size):
        points_inside_circle += 1
print("Approximate value of pi is {}" .format(compute_pi(points_inside_circle,points_inside_square)))

  估计的$\pi$值和生成的散点图。

基于蒙特卡罗方法的model-free RL算法

  蒙特卡罗方法应用于Value Function的求解过程中。我们已经知道，Value Function是在基于某个策略的前提下，对状态的好坏进行评估的函数。Monte Calo用于值估计的思想很简单：对于状态$s_t$，要确定$s_t$的价值，也就是$s_t$之后直到游戏结束的累计回报，只需要不停地玩游戏，记录每次从$s_t$出发，直到结束所得的分数。比如访问了状态 $s_t$ 20次，累计回报是

9, 14, 18, 13, 11, 20, 17, 15, 10, 16, 18, 16, 6, 13, 10, 20, 19, 1, 12, 10
sum = 221

则$V^{\pi }(s_t)$可以近似为
$$\frac{221}{20}=10.15$$

  对Q函数的估计也是相似的，记录从状态$s_t$出发，采取动作$a$之后，获得的累计回报，取其平均值，作为$Q^{\pi }(s_t,a)$的估计。

  当然，还有一个问题：同一次游戏中，可能多次访问同一个状态，如何记录多次访问前后的累计回报呢？两个方法：

• 首次访问 First Visit Monte Calo 每局游戏只记录第一次访问$s_t$之后的累计回报
• 每次访问 Every Visit Monte Calo 每局游戏记录每次访问$s_t$之后的累计回报

编程实现

  先简单介绍一下游戏环境Blackjack-v0，就是21点。21点的规则不多介绍，大体上就是比较谁的牌面值之和最接近21。

  状态空间Observation向量的长度是3，表示闲家分数、庄家分数、是否将Ace当做11来计算。动作空间就两个取值，Hit或Stand，也就是叫牌或者不叫牌。需要注意的是，21点游戏中，两张牌面值之和最小不是2，是4。因为两张A看做$11+1=12$更有优势，所以最小的数是$2+2=4$。

  定义一个简单策略：当前牌面值之和＜20就继续叫牌，否则就不叫牌。

def sample_policy(observation):
    '''
    如果当前牌面值>=20，就不再叫牌（Stand）
    如果当前牌面值<20,继续叫牌（Hit）
    '''
    # observation len=3,分别是闲家分数、庄家分数、是否将A当做11
    score, dealer_score, usable_ace = observation
    return 0 if score >= 20 else 1

  利用这个简单策略玩游戏，记录游戏过程中每一回合的状态、动作、回报数据。

def generate_episode(policy, env):
    '''
    玩一局游戏，收集状态信息、动作信息和reward
    '''
    states, actions, rewards = [], [], []
    observation = env.reset()
    while True:
        states.append(observation)
        # 根据策略函数，确定采取的动作
        action = sample_policy(observation)
        actions.append(action)
        observation, reward, done, info = env.step(action)
        rewards.append(reward)
        if done:
            break
    return states, actions, rewards

  实现首次访问的蒙特卡罗算法。

def first_visit_mc_prediction(policy, env, n_episodes):
    '''
    
    '''
    value_table = defaultdict(float)
    N = defaultdict(int)
    for _ in range(n_episodes):
        states, _, rewards = generate_episode(policy, env)
        returns = 0
        for t in range(len(states) - 1, -1, -1):
            R = rewards[t]
            S = states[t]
            returns += R
            if S not in states[:t]:
                N[S] += 1
                value_table[S] += (returns - value_table[S]) / N[S]
    return value_table

  完整代码，最后画出Value Function。

import numpy
import gym
from matplotlib import pyplot
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from collections import defaultdict
from functools import partial
%matplotlib inline
plt.style.use('ggplot')


## Blackjack Environment
env = gym.make('Blackjack-v0')


def sample_policy(observation):
    '''
    如果当前牌面值>=20，就不再叫牌（Stand）
    如果当前牌面值<20,继续叫牌（Hit）
    '''
    # observation len=3,分别是闲家分数、庄家分数、是否将A当做11
    score, dealer_score, usable_ace = observation
    return 0 if score >= 20 else 1

def generate_episode(policy, env):
    '''
    玩一局游戏，收集状态信息、动作信息和reward
    '''
    states, actions, rewards = [], [], []
    observation = env.reset()
    while True:
        states.append(observation)
        # 根据策略函数，确定采取的动作
        action = sample_policy(observation)
        actions.append(action)
        observation, reward, done, info = env.step(action)
        rewards.append(reward)
        if done:
            break
    return states, actions, rewards

def first_visit_mc_prediction(policy, env, n_episodes):
    '''
    
    '''
    value_table = defaultdict(float)
    N = defaultdict(int)
    for _ in range(n_episodes):
        states, _, rewards = generate_episode(policy, env)
        returns = 0
        for t in range(len(states) - 1, -1, -1):
            R = rewards[t]
            S = states[t]
            returns += R
            if S not in states[:t]:
                N[S] += 1
                value_table[S] += (returns - value_table[S]) / N[S]
    return value_table

def plot_blackjack(V, ax1, ax2):
    player_sum = numpy.arange(12, 21 + 1)
    dealer_show = numpy.arange(1, 10 + 1)
    usable_ace = numpy.array([False, True])
    state_values = numpy.zeros((len(player_sum),
                                len(dealer_show),
                                len(usable_ace)))
    for i, player in enumerate(player_sum):
        for j, dealer in enumerate(dealer_show):
            for k, ace in enumerate(usable_ace):
                state_values[i, j, k] = V[player, dealer, ace]
    print(np.shape(state_values))
    X, Y = numpy.meshgrid(player_sum, dealer_show)
    ax1.plot_wireframe(X, Y, state_values[:, :, 0])
    ax2.plot_wireframe(X, Y, state_values[:, :, 1])
    for ax in ax1, ax2:
        ax.set_zlim(-1, 1)
        ax.set_ylabel('player sum')
        ax.set_xlabel('dealer showing')
        ax.set_zlabel('state-value')
        
fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8), subplot_kw={'projection': '3d'})
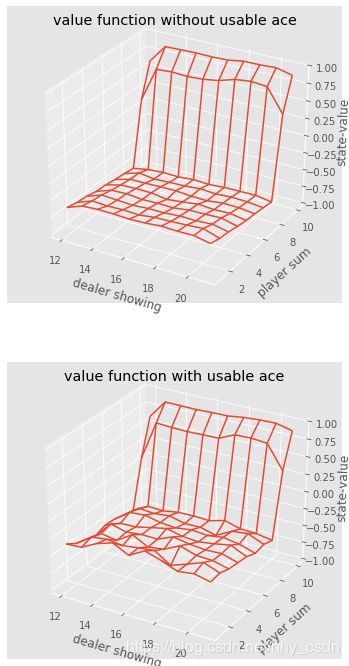
axes[0].set_title('value function without usable ace')
axes[1].set_title('value function with usable ace')

value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000)

plot_blackjack(value, axes[0], axes[1])

  价值函数三维函数。由于observation是三维向量（闲家牌值，庄家牌值，是否把A当做11），所以把最后一维拆开来画。第一张图是 不把A当做11（即，without usable Ace）的情况下把前两维（闲家牌值，庄家牌值）画出来的，第二张图是with usable Ace的情况下画的。