TensorFlow.js学习笔记—曲线拟合
这个DEMO是参考了TensorFlow.js官网的教程,融合了一些自己的实现。
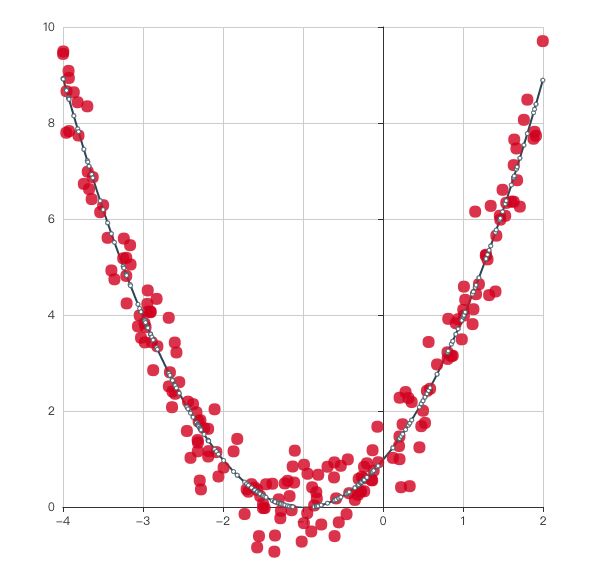
这是一个二次函数曲线的拟合,效果我个人觉得还可以。
为了实现这个效果,首先我们得有要有数据,不然我们拟合什么?数据就是下图所示的这些散点。
为了巧妇能有米来炊,我们首先得要实现一个产生数据的函数。
function generateData(numPoints, coeff, sigma = 0.5) {
return tf.tidy(() => {
const [a, b, c] = [
tf.scalar(coeff.a),
tf.scalar(coeff.b),
tf.scalar(coeff.c)
];
const xs = tf.randomUniform([numPoints], -4, 2);
const ys = a.mul(xs.pow(tf.scalar(2, 'int32')))
.add(b.mul(xs))
.add(c)
//添加噪声
.add(tf.randomNormal([numPoints], 0, sigma));
/*
//数据归一化
const ymin = ys.min();
const ymax = ys.max();
const yrange = ymax.sub(ymin);
const ysNormalized = ys.sub(ymin).div(yrange);
*/
return {
xs,
ys: ys
};
})
}
我们首先是要拿到你所要拟合的函数的系数,本例中所要拟合的函数方程是 y = x 2 + 2 x + 1 y=x^2+2x+1 y=x2+2x+1,所以 a = 1 , b = 2 , c = 1 a=1,b=2,c=1 a=1,b=2,c=1。
然后我们使用tf.randomUniform方法产生指定数量,指定范围且均匀分布的点的X坐标。
接下来我们就要通过计算得出点的Y坐标,如下面代码所示。
const ys = a.mul(xs.pow(tf.scalar(2, 'int32')))
.add(b.mul(xs))
.add(c)
到这里,y坐标已经被计算出来了,然而我们还需要为它们添加噪声,不然我们就没有什么好拟合的了。
.add(tf.randomNormal([numPoints], 0, sigma));
tf.randomNormal和上面的tf.randomUniform一样都是产生随机数,不同在于tf.randomNormal生成的数据是正态分布的。
我注释掉的那段代码是对y值进行归一化操作,实际上归一化能够提高效率,我只是为了数据看起来更符合直觉去掉了它,在实际应用中还是最好保留。
数据产生完了,下面就是重头戏–模型的构造与训练。
1.声明变量
首先,我们要声明一些变量(就是函数的系数),用以存放最终训练完成后拟合出的函数系数。不过一开始我们只是给他们赋成随机数。
const a = tf.varible(tf.scalar(Math.random()));
const b = tf.varible(tf.scalar(Math.random()));
const c = tf.varible(tf.scalar(Math.random()));
2.构建一个模型
一个模型其实就是一个函数,你给出一个输入,模型便会给你一个你期望中的结果。那么在本例中,模型便是要计算 y = x 2 + 2 x + 1 y=x^2+2x+1 y=x2+2x+1。
function predict(x) {
return tf.tidy(() => {
return a.mul(x.pow(tf.scalar(2, 'int32')))
.add(b.mul(x))
.add(c);
});
}
如果你写到这里就直接运行的话,那么你得到的散点跟绘制出的曲线根本没有什么关系,原因很简单,因为在这个时候模型的系数依然还是随机数。所以我们还需要对模型进行训练。
3.训练模型
- 定义损失函数:
在这个例子中,我使用了均方误差作为损失函数。代码如下
function loss(prediction, labels) {
const squareMeanError = prediction.sub(labels).square().mean();
return squareMeanError;
}
- 定义优化器:
在这个例子里面,我使用了SGD(随机梯度下降)。TensorFlow.js提供了简便的方法来实现SGD,我们就不用操心要自己来写许多繁杂的数学计算了。在这里,我使用了tf.train.sgd,这个方法需要一个learning rate 作为参数。
learning rate 控制了当改进预测值时需要对函数系数做出的变动大小。一个低的learning rate 将会使学习过程变得更缓慢,因为需要更多的迭代次数。一个大的learning rate 虽然能使学习过程变快,但是可能导致模型总在正确值附近摇摆。
const learningRate = 0.5;
const optimizer = tf.train.sgd(learningRate);
- 定义训练迭代
我们定义完了损失函数和优化器之后,我们就可以构建训练的迭代过程了。这个过程就是迭代的运行随机梯度下降来改进模型的参数从而最小化损失。
async function train(xs, ys, numIterations) {
for (let iter = 0; iter < numIterations; iter++) {
optimizer.minimize(() => {
const pred = predict(xs);
return loss(pred, ys);
});
await tf.nextFrame();
}
}
参数中的xs,ys就是上面生成的数据,numIterations就是迭代次数。
在for循环中,我们执行优化器的minimize方法。
minimize方法接受一个函数作为参数,这个函数需要做两件事:
- 使用predict(也就是模型)为所有的x都计算出y值。
- 返回这些y值的均方误差(使用前面定义的loss函数计算)
minimize方法将会自动的修改被这个函数调用的变量(也就是函数参数),目的是最小化损失。
训练的迭代过程运行完后,a、b、c将会变为模型经过numIteration次随机梯度下降后所学习到的值。
最后运行就能看到文章开头图片的效果了,DEMO完整的代码,在这里。