高性能计算简介

高性能计算简介

---

高性能计算

高性能计算（High Performance Computing，HPC）是一个综合的领域，包括各种并行编程范式、与各范式相关的编程语言和应用编程接口（Applicaiton Programming Interface，API）、定制的软件工具等。

HPC有助于更快、更加准确（对于模拟类的应用，例如天气预报、汽车碰撞测试中的计算力学、或者其他更加复杂的现象的模拟）的运行程序

• 在超级计算机上利用模型进行模拟
• 能够快速地获取结果并没有延迟：天气状况、股票行情
• 处理大数据集：基因组分析或基因组系

大数据的特性

• 数据量（Volume）
• 多样性（Variety）、异构数据
• 生成速度（Velocity）不断地从传感器中获取数据
• 价值（Value）并非模拟数据而是有价值的真实数据

并行编程范式：MPI和MapReduce

• MPI（消息传递接口编程） MPI对硬件或网络没有鲁棒性，但是为程序员提供了一个灵活的编程框架
• MapReduce（对应的免费开源版本Hadoop）编程。MapReduce包含一个底层架构，能够应对网络或硬件错误，但是与MPI相比，编程方式非常有限。

粒度

粒度是指代码中能够被并行化的部分所占的比例。

• 细粒度并行（fine-grained parellelism）:在同一个任务内变量级别并行，多数的扩展指令集都支持SIMD指令。细粒度并行也依赖于显卡的GPU片段
• 中粒度并行（mid-grained parallelism）：同一个程序中的线程级别并行
• 粗粒度并行（coarse-grained parallelism）：大数据块计算完成之后，通常会进行有限次数的数据传输。

内存和网络

我们将并行计算机分为两类：基于共享内存的并行机和基于分布式内存的并行机

通常，在一个多核处理器上，所有核使用同一个存储器组（memory bank），这种架构将所有的核视为独立的处理单元，因此也称为共享内存多处理器（Symmetric Shared Memory Multiprocessor，SMP）。

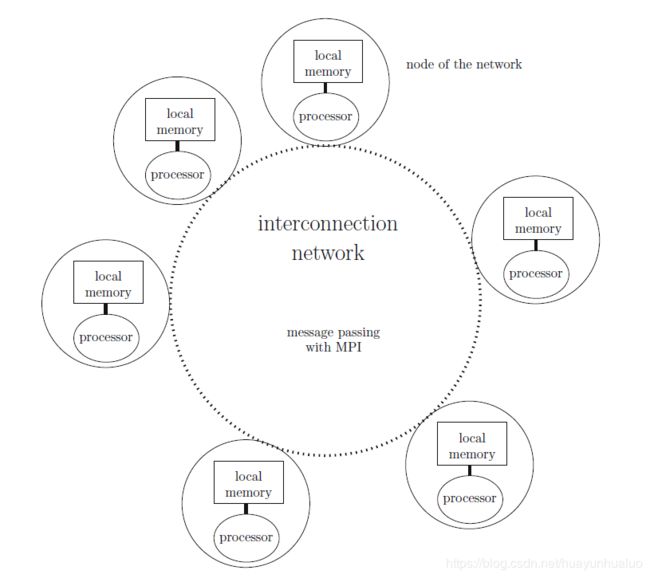
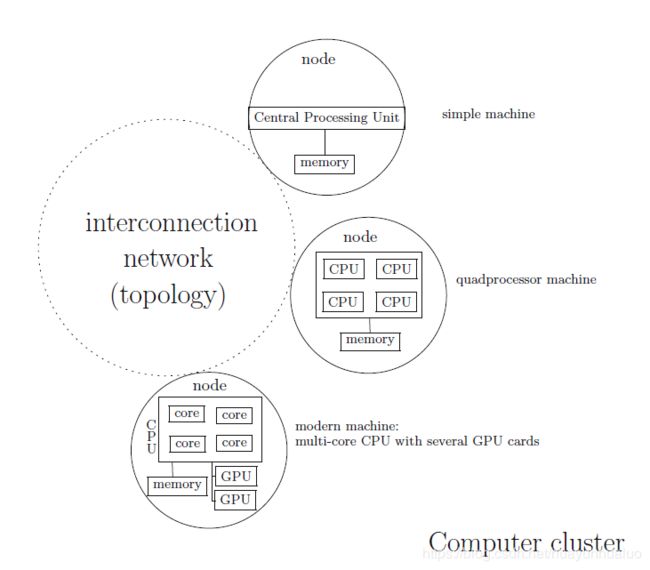
与共享内存架构相反，基于分布式内存的并行集群通过互联网将每个独立的计算机连接起来。

消息可以通过点对点的方式或者中间节点为路由的方式进行交换。

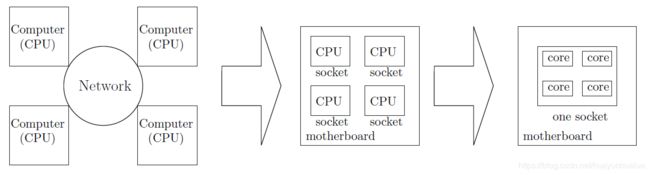
计算机体系的发展，从一个小型的计算机到多处理器计算机到多核计算机。

在分布式架构中，当访问另外一个进程的时候，需要显式的调用内存访问操作，并通过互联网进行信息交换。

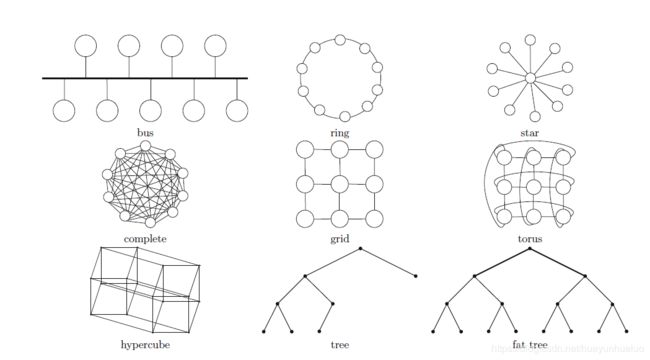
互联网的三个特性

• 延迟：一个通信所需要的时间
• 带宽：通信链路上的数据的传输速率
• 拓扑：互联网络的物理结构

加速比

令$t_{seq}$表示顺序程序的运行时间，$t_p$表示对应的并行程序在$P$个处理器上的运行时间。令$t_1$表示并行程序在$P=1$个处理器上的运行时间。

加速比
$$speedup(P)=\frac{t_{seq}}{t_P}$$
通常由$\frac{t_{seq}}{t_P}\simeq \frac{t_1}{t_P}$

效率：
$$e=\frac{speedup(P)}{P}=\frac{t_{seq}}{P\times t_P}$$
低效率意味着高并行负载，最佳的线性加速比意味着最大的效率，即为1.

扩展性
$$scalability(O,P)=\frac{t_o}{t_P}O<P$$

扩展性和等效效率分析

一个可扩展的并行算法能够很容易的运行在任意$P$个处理器上。对于给定的问题规模$n$，当我们增加处理器个数$P$时，程序的效率会呈现下降趋势。因此为了维持一个好的加速比，当$P$增加时，我们同样的增加输入的数据规模$n$。更加确切的说，参数$n$和$P$是相关的。

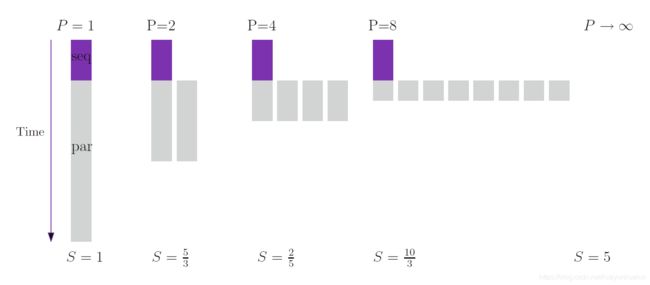
Amdahl定律：描述数据规模固定时渐近加速比的变化趋势

令${\alpha }_{par}$表示代码中可并行化部分所占的比例，${\alpha }_{seq}$表示本质上串行所占的比例，且${\alpha }_{par}+{\alpha }_{seq}=1$
$$t_p={\alpha }_{seq}{t}_1+(1-{\alpha }_{seq})\frac{t_1}{P}={\alpha }_{par}\frac{t_1}{P}+{\alpha }_{seq}{t}_1$$
假设$t_{seq}=t_1$
$$speedup(P)=\frac{t_1}{t_P}=\frac{({\alpha }_{par}+{\alpha }_{seq})t_1}{({\alpha }_{seq}+\frac{{\alpha }_{par}}{P})t_1}=\frac{1}{{\alpha }_{seq}+\frac{{\alpha }_{par}}{P}}$$
当处理器数量趋近于无穷$P\to \infty$ 因此
$$\underset{P\to \infty }{\lim }speedup(P)=\frac{1}{{\alpha }_{seq}}=\frac{1}{1-{\alpha }_{par}}$$
因此加速是上限由代码中不可并行化的部分决定的。

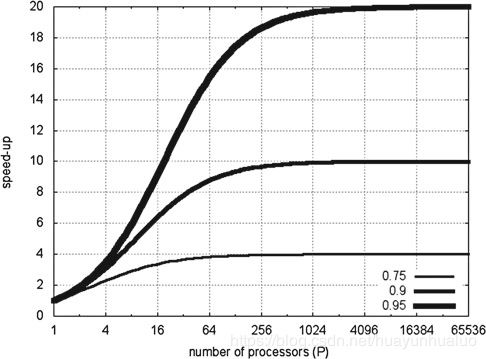
定理：Amdahl定律给出了一个并行程序的最优渐近加速比，即$speedup=\frac{1}{{\alpha }_{seq}}=\frac{1}{1-{\alpha }_{par}}$

Amdahl定律假设输入的数据规模是固定的。

当使用$P$个计算机并行地处理$n$个数据时，我们隐含的假设计算机处理$n$个数据，那么$\frac{n}{P}$数据可以存储在RAM中，然而，如果使用一个计算机处理$n$个数据，那么$\frac{n}{P}$可以存储在RAM中，剩余的$\frac{n-1}{P}$个数据存储在硬盘中，并且硬盘的处理速度要远远小于RAM的访问速度。这样。对于大数据集，我们可以通过将数据存储在每个计算机的本地RAM中的方式来观察超线程加速比。

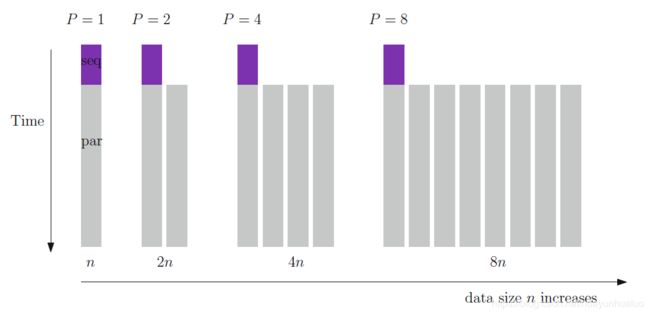
Gustafson定律：可扩展的加速比

加速比
$$speedup(P)=\frac{t_{seq}+P\times t_{par}}{t_{seq}+t_{par}}$$
根据定义$\frac{t_{seq}}{t_{seq}+t_{par}}={\alpha }_{seq},\frac{t_{par}}{t_{seq}+t_{par}}={\alpha }_{par}$
$$speedu{p}_{Gustafson}(P)={\alpha }_{seq}+P\times {\alpha }_{par}$$
定理：Gustafson定律表明了最优加速比渐近于$speedup(P)=P\times {\alpha }_{par}$

在串行计算机上模拟并行机

理论上，通过在串行计算机上模拟并行程序，能够得到的结论

1. 最大加速比时$O(P)$，$P$表示处理器个数
2. 能为某个问题生成下界，因为利用并行方法解决一个问题的最好的时间复杂度时$\Omega (\frac{C_{seq}}{P})$，$\Omega (C_{seq})$表示串行执行时间的复杂度下界。

大数据和并行输入/输出

为了处理大数据，需要读取或存储超大文件，或者是大量的小文件，这些操作称为输入/输出，为了避免这种非常耗时的编程任务，人们开发出多个并行文件系统用来处理各种复杂的I/O操作。例如MapReduce，是基于Google文件系统开发的（HDFS，Hadoop分布式文件系统）

分布式系统常见的误区

• 网络是可靠的
• 延迟为零
• 带宽无限大
• 网络是安全的
• 网络的拓扑是静态的
• 只有一个网络管理员
• 数据传输和程序迁移不需要成本
• 网络是同构的