PRML读书笔记——图模型

本章主要分析贝叶斯网络、条件独立、马尔科夫随机场和图模型的推断

0 前言

概率图模型：用概率分布的图形表示变量之间的依赖关系

⼀个图由结点（nodes）和它们之间的链接（links）组成。在概率图模型中，每个结点表⽰⼀个随机变量（或⼀组随机变量），链接表⽰这些变量之间的概率关系。这样，图描述了联合概率分布在所有随机变量上能够分解为⼀组因⼦的乘积的⽅式，每个因⼦只依赖于随机变量的⼀个⼦集。

1 贝叶斯网络

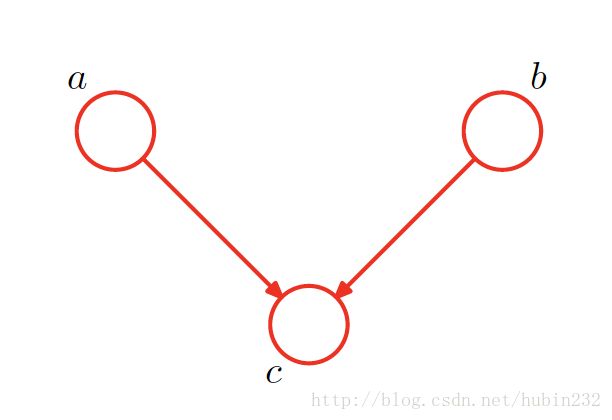
贝叶斯网络是一个有向图模型，一个简单的示例如下：

就上图而言，链接的起点就是条件概率的条件中的随机变量对应的结果，因此上图对应概率形式可以表示如下：

p(x1)p(x2)p(x3)p(x4|x1,x2,x3)p(x5|x1,x3)p(x6|x4)p(x7|x4,x5)

显然，真正传递出图表示的概率分布的有趣信息的是图中链接的缺失。

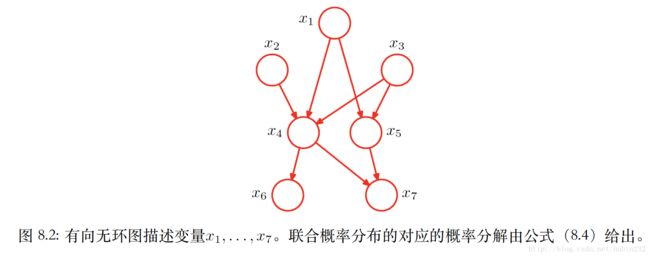
下面给出更一般的形式，对于一个有K个结点的图，联合概率为：

p(x)=∏k=1Kp(xk|pak)

其中， pak 表示 xk 的父结点的集合， x={x1,...,xk} 。这个关键的方程表示有向图模型的联合概率分布的分解属性。

这里，贝叶斯网络对应的有向图是有向无环图（DAG）。这等价于存在一个对所有点的排序，使得不存在从某个结点到序号较小的结点的链接。

多项式回归的例子

多项式回归的概率形式为：

p(t,w|x,α,σ2)=p(w|α)∏n=1Np(tn|w,xn,σ2)

一般而言，会用给对应结点加上阴影的方式表示观测变量。因此，以t为观测变量，上述概率形式用图模型表示如下：

生成式模型的例子

这里分析的是图模型与采样方法的关系。对应于⼀个有向⽆环图。我们假设变量已经进⾏了排序，从⽽不存在从某个结点到序号较低的结点的链接。换句话说，每个结点的序号都⼤于它的⽗结点。我们的⽬标是从这样的联合概率分布中取样 x1ˆ,...,xkˆ 。这里，假设我们已知第一个样本的初始概率分布。那么，图模型对应的就是祖先采样。

祖先采样：我们⾸先选出序号最⼩的结点，按照概率分布 p(x1) 取样，记作 x1 。然后，我们顺序计算每个结点，使得对于结点n，我们根据条件概率 p(xn|pan) 进⾏取样，其中⽗结点的变量被设置为它们的取样值。注意，在每个阶段，这些⽗结点的变量总是可以得到的，因为它们对应于已经采样过的序号较⼩的结点。⼀旦我们对最后的变量 xK 取样结束，我们就达到了根据联合概率分布取样的⽬标。为了从对应于变量的⼦集的边缘概率分布中取样，我们简单地取要求结点的取样值，忽略剩余结点的取样值。

离散变量的例子

对于一个有K个可能状态的一元离散变量 x ，概率 p(x|u) 为：

p(x|u)=∏k=1Kuxkk

其中，参数 u=(u1,...,uK)T ，由于限制条件 ∑kuk=1 的存在，实际上定义这个概率分布，只需要K-1个参数即可。

这里讨论参数个数是因为，对离散变量采用图模型表示时，隐含的参数数量随着结点个数的增长迅速增长。

比如，考虑一般的情形，如果我们有M个离散变量 x1,...,xM ，我们可以用有向图来对联合概率分布建模，每个变量一个结点。假如考虑链式的链接形式（如下图），那么整个图的概率分布所需要的参数数量为 K−1+(M−1)K(K−1) 。

有效减少模型中独立参数的方法有两个：

（1）参数共享。比如为参数引入先验，或者对每个结点包含的参数增加约束

（2）对条件概率分布使用参数化的模型，而不是使用条件概率的完整表示。

2 条件独立

条件独立

多变量概率的分布的一个重要概念是条件独立，这在图模型中很容易看出来，实现联合概率分布条件独立的方法被称为d-划分(d-separation)

所谓的条件独立，是指：

考虑三个变量 a,b,c ，如果其联合概率存在下面的形式：

p(a,b|c)=p(a|b,c)p(b|c)=p(a|c)p(b|c)

那么，我们说在给定c的条件下，a条件独立于b

三种基本情况

（1）tail-to-tail

假设以变量c为条件，则有：

p(a,b|c)=p(a,b,c)P(c)=p(a|c)p(b|c)

显然，此时a，b相互独立。

假设现在没有变量是观测变量，则有：

p(a,b)=∑cp(c)p(a|c)p(b|c)

显然，此时a，b不一定相互独立。

（2）tail-to-head

假设以c为条件，则有：

p(a,b|c)=p(a,b,c)p(c)=p(a)p(c|a)p(b|c)p(c)=p(a|c)p(b|c)

显然，此时，a和b关于条件c相互独立。

假设没有观测变量，则有：

p(a,b)=p(a)∑cp(c|a)p(b|c)=p(a)p(b|a)

此时，a，b不相互独立。

（3）head-to-head

假设以c为条件，则有：

p(a,b|c)=p(a,b,c)p(c)=p(a|c)p(b|c)p(c|a,b)p(c)

显然，此时，a，b不相互独立。

假设没有观测变量，则有：

p(a,b)=∑cp(a)p(b)p(c|a,b)=p(a)p(b)

此时，显然，a，b相互独立。

d-划分

我们现在给出有向图d-划分性质的⼀个⼀般的叙述。考虑⼀个⼀般的有向图，其中A,B,C是任意⽆交集的结点集合（它们的并集可能⽐图中结点的完整集合要⼩）。我们希望弄清楚，⼀个有向⽆环图是否暗⽰了⼀个特定的条件依赖表述 A独立B|C 。为了解决这个问题，我们考虑从A中任意结点到B中任意结点的所有可能的路径。我们说这样的路径被“阻隔”，如果它包含⼀个结点满⾜下⾯两个性质中的任何⼀个。

（1）路径上的箭头以头到尾或者尾到尾的⽅式交汇于这个结点，且这个结点在集合C中。

（2）箭头以头到头的⽅式交汇于这个结点，且这个结点和它的所有后继都不在集合C中。

如果所有的路径都被“阻隔”，那么我们说C把A从B中d-划分开，且图中所有变量上的联合概率分布将会满⾜ A独立B|C 。

上图是一个例子，左边的图中，a和b不独立；右边的图中， a独立b|f

朴素贝叶斯模型的图模型表示：

对应的表达式为：

p(D|u)=∏n=1Np(xn|u)

3 马尔科夫随机场

上面分析的是有向图模型，下面考虑无向图，他表示一个分解方式，也表示一组条件独立关系。而马尔科夫随机场是一个无向图模型。

条件独立性质

分析条件独立，主要就是看路径是否被阻隔。假设在无向图中，有三个结点集合，记作 A,B,C ，我们考虑条件独立性质 A独立B|C

我们考虑连接集合A的结点和集合B的结点的所有可能路径。如果所有这些路径都通过了集合C中的⼀个或多个结点，那么所有这样的路径都被“阻隔”，因此条件独⽴性质成⽴。然⽽，如果存在⾄少⼀条未被阻隔的路径，那么性质条件独⽴的性质未必成⽴，或者更精确地说，存在⾄少某些对应于图的概率分布不满⾜条件独⽴性质。

分解性质

所谓的分解性质，就是将联合概率分布 p(x) 表示为在图的局部范围内的变量集合上定义的函数的乘积。

考虑两个结点 xi 和 xj ，它们不存在链接，那么给定图中的所有其他结点，这两个节点条件独立，有：

p(xi,xj|x/{i,j})=p(xi|x/{i,j})p(xj|x/{i,j})

所以，联合概率分布的分解要让两个节点不出现在同一个因子中，从而让属于这个图的所有可能的概率分布都满足条件独立性质。

因此引入“团”的概念。它被定义为图中结点的⼀个⼦集，使得在这个⼦集中的每对结点之间都存在链接。换句话说，团块中的结点集合是全连接的。此外，⼀个最⼤团块（maximal clique）是具有下⾯性质的团块：不可能将图中的任何⼀个其他的结点包含到这个团块中⽽不破坏团块的性质。

上图最大团有两个，分别是 {x1,x2,x3} 和 {x2,x3,x4} 。

有了团的概念后，我们考虑图中联合概率的分解。这里将团块记作C，团块中的变量集合记作 xC 。这样，联合概率分布可以写成图的最大团块的势函数：

p(x)=1Z∏CψC(xC)

这里， ψ 是势函数，而Z是一个归一化常数，等于：

Z=∑x∏CψC(xC)

这样，就将联合概率和势函数（能量函数）关联起来了。

这里，归一化常数的存在是无向图的主要缺点之一。因为难以计算，我们可以考虑先计算为归一化的联合概率分布，最后再显示地归一化所有边缘概率。

为了将势函数严格限制为大于零，一般讲势函数表示为指数形式：

ψC(xC)=exp(−E(xC))

其中， E(xC) 被称为能量函数。而其具体的形式则根据实际情况具体分析设计。

图像去噪

这里列举图像去噪的例子来使用势能函数，

我们令观测的噪声图像通过一个二指像素值 yi∈{−1,+1} 组成的数组来描述，而未知的无噪声图像，由二值像素值 xi∈{−1,+1} 描述。现在，该问题对应的马尔科夫随机场可以由下图表示：

显然，这幅图的最大团块是 {xi,xj} 和 {xi,yi} 。因为能量函数是最大团结点的函数，可以设计如下：

E(x,y)=h∑ixi−β∑{i,j}xixj−η∑ixiyi

这里，相邻的像素颜色相近则能量较小；观测值与真实值相近则能量小。

因此，x和y上的联合概率分布可以表示为：

p(x,y)=1Zexp{−E(x,y)}

与有向图的关系

有向图可以转化为无向图。这里的转化需要保留相关的概率形式。

转化步骤是：

（1）在图中每个结点的所有⽗结点之间添加额外的⽆向链接（这个过程也被称为伦理）

（2）去掉原始链接的箭头，得到道德图

（3）将道德图的所有的团块势函数初始化为1

（4）拿出原始有向图中所有的条件概率分布因⼦，将它乘到⼀个团块
势函数中去

4 图模型中的推断

推断问题就是指，图中的一些结点被限制为观测值，需要计算其他结点中的一个或多个子集的后验概率分布。

链推断

这里主要考虑如下的无向图：

它对应的联合概率分布为：

p(x)=1Zψ1,2(x1,x2)ψ2,3(x2,x3)...ψN−1,N(xN−1,xN)

现在寻找 p(xn) 的边缘概率分布，其中 xn 是链子上的具体结点。由于没有观测结点，则对应的边缘概率分布为:

p(xn)=∑x1...∑xn−1∑xn+1...∑xNp(x)

进一步整合，可得：

p(xn)=1Z⎡⎣⎢⎢∑xn−1ψn−1,n(xn−1,xn)...⎡⎣⎢⎢∑x2ψ2,3(x2,x3)⎡⎣⎢⎢∑x1ψ1,2(x1,x2)⎤⎦⎥⎥⎤⎦⎥⎥...⎤⎦⎥⎥⎡⎣⎢⎢∑xn+1ψn,n+1(xn,xn+1)...⎡⎣⎢⎢∑xNψN−1,N(xN−1,xN)⎤⎦⎥⎥...⎤⎦⎥⎥

显然，这个公式可以分解为两个音字的乘积乘以归一化系数，如下：

p(xn)=1Zuα(xn)uβ(xn)

其中， uα(xn) 是从结点 xn−1 到结点 xn 的沿着链向前传递的信息；而 uβ(xn) 从结点 xn+1 到结点 xn 沿着链向后传递的信息。它们都可以递归求解，分别如下：

uα(xn)=∑xn−1ψn−1,n(xn−1,xn)⎡⎣⎢⎢∑xn−2...⎤⎦⎥⎥=∑xn−1ψn−1,n(xn−1,xn)uα(xn−1)

uβ(xn)=∑xn1ψn,n+1(xn,xn+1)⎡⎣⎢⎢∑xn+2...⎤⎦⎥⎥=∑xn+1ψn,n+1(xn,xn+1)uβ(xn+1)

树结构

在无向图中，树的定义是：任意一对节点之间有且只有一条罗京。于是这样的图没有环

在有向图中，树的定义是：有一个没有父结点的结点，被称为根，其他所有的结点都有一个父节点。

在有向图中，多树的定义是：存在具有多个⽗结点的结点，但是在任意两个结点之间仍然只有⼀条路径（忽略箭头⽅向）

因子图

因子图就是在表示变量的结点的基础上，引入额外的结点表示因子本身。

首先，定义一组变量上的联合概率分布可以写成因子的乘积形式：

p(x)=∏sfs(xs)

那么，最上面那个图的概率表示形式为：

p(x)=fa(x1,x2)fb(x1,x2)fc(x2,x3)fd(x3)

加和-乘积算法

因子图可以用来表示有向图和无向图的概率分布，通过因子图统一出算法进行计算。

加和-乘积算法的目的：

（1） 得到一个高效的精确推断算法来寻找边缘概率

（2）在需要求解多个边缘概率的情况下，计算可以高效地共享

因子图把概率依赖关系看做是信息的传递，用传递的思想求解边缘概率。

以下图为例说明：

这里存在两种信息的传递，即从因子节点到变量节点、从变量结点到因子节点。加和-乘积算法就是对这两种信息传递提出了固定的表达形式。

加和-乘积算法：

对于因子节点，如果自身是叶子结点，则将自身f(x)传递给父节点；如果自身是非叶子结点，则将受到的信息与自身f(x)相乘再求和，发送给父节点

对于变量结点，如果自身是叶子节点，则默认自身信息为1，发送给父节点；如果自身是非叶子节点，就将收到的信息直接相乘，发给父节点。

这里，父节点和叶子节点是相对的。如果要求的是 xi 的边缘概率，则以 xi 为根节点，形成树，得到对应的叶子节点和信息传递的路径，再根据加和—乘积算法计算。

对于上图的例子，如果想求 x3 的边缘概率，则我们以 x3 根节点，信息传递如左下。则有：

ux1→fa(x1)=1

ufa→x2(x2)=∑x1fa(x1,x2)

ux4→fc(x4)=1

ufc→x2(x2)=∑x4fc(x2,x4)

ux2→fb(x2)=ufa→x2(x2)ufc→x2(x2)

ufb→x3(x3)=∑x2fb(x2,x3)ux2→fb(x2)

同理，可以将信息传递回到各个叶节点，公式如下：

ux3→fb(x3)=1

ufb→x2(x2)=∑x3fb(x2,x3)

ux2→fa(x2)=ufb→x2(x2)ufc→x2(x2)

ufa→x1(x1)=∑x2fa(x1,x2)ux2→fa(x2)

ux2→fc(x2)=ufa→x2(x2)ufb→x2(x2)

ufc→x4(x4)=∑x2fc(x2,x4)ux2→fc(x2)

最大加和算法

加和-乘积算法使得我们能够将联合概率分布p(x)表⽰为⼀个因⼦图，并且⾼效地求出成分变量上的边缘概率分布。有两个其他的⽐较常见的任务，即找到变量的具有最⼤概率的⼀个设置，以及找到这个概率的值。这两个任务可以通过⼀个密切相关的算法完成，这个算法被称为最⼤加和。

其实，这里本质就是求解：

xmax=argmaxxp(x)

以及对应的概率分布值：

p(xmax)=maxxp(x)

具体求解可以采用反向跟踪法，这个算法应用的典型代表应该是隐马尔科夫链中的隐含状态的最可能序列，那个问题采用的是Viterbi算法。