图文并茂的PCA教程
声明:
- 参考:PCA数学原理、维基百科
PCA——主成分分析
简介
PCA全称Principal Component Analysis,即主成分分析,是一种常用的数据降维方法。它可以通过线性变换将原始数据变换为一组各维度线性无关的表示,以此来提取数据的主要线性分量。
z = w T x z = w^Tx z=wTx
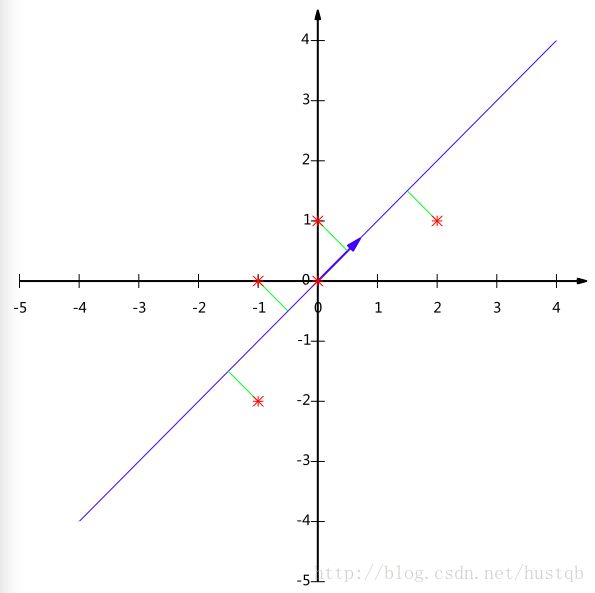
其中,z为低维矩阵,x为高维矩阵,w为两者之间的映射关系。假如我们有二维数据(原始数据有两个特征轴——特征1和特征2)如下图所示,样本点分布为斜45°的蓝色椭圆区域。PCA算法认为斜45°为主要线性分量,与之正交的虚线是次要线性分量(应当舍去以达到降维的目的)。
划重点:
- 线性变换=>新特征轴可由原始特征轴线性变换表征
- 线性无关=>构建的特征轴是正交的
- 主要线性分量(或者说是主成分)=>方差加大的方向
- PCA算法的求解就是找到主要线性分量及其表征方式的过程
相应的,PCA解释方差并对离群点很敏感:少量原远离中心的点对方差有很大的影响,从而也对特征向量有很大的影响。
线性变换
一个矩阵与一个列向量A相乘,等到一个新的列向量B,则称该矩阵为列向量A到列向量B的线性变换。
我们希望投影后投影值尽可能分散,而这种分散程度,可以用数学上的方差来表述。 V a r ( a ) = 1 m ∑ i = 1 m ( a i − μ ) 2 Var(a) = \frac 1m \sum_{i=1}^m(a_i - \mu)^2 Var(a)=m1i=1∑m(ai−μ)2即寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大。
解释:方差越大,说明数据越分散。通常认为,数据的某个特征维度上数据越分散,该特征越重要。
对于更高维度,还有一个问题需要解决,考虑三维降到二维问题。与之前相同,首先我们希望找到一个方向使得投影后方差最大,这样就完成了第一个方向的选择,继而我们选择第二个投影方向。如果我们还是单纯只选择方差最大的方向,很明显,这个方向与第一个方向应该是“几乎重合在一起”,显然这样的维度是没有用的,因此,应该有其他约束条件——就是正交
解释:从直观上说,让两个字段尽可能表示更多的原始信息,我们是不希望它们之间存在(线性)相关性的,因为相关性意味着两个字段不是完全独立,必然存在重复表示的信息。
字段在本文中指,降维后的样本的特征轴
数学上可以用两个字段的协方差表示其相关性: C o v ( a , b ) = 1 m ∑ i = 1 m ( a i − μ a ) ( b i − μ b ) Cov(a, b) = \frac 1m \sum_{i=1}^m (a_i - \mu_a)(b_i - \mu_b) Cov(a,b)=m1i=1∑m(ai−μa)(bi−μb)当协方差为0时,表示两个字段线性不相关。
总结一下,PCA的优化目标是:
将一组N维向量降为K维(K大于0,小于N),其目标是选择K个单位正交基,使得原始数据变换到这组基上后,各字段两两间协方差为0,而字段的方差则尽可能大。
所以现在的重点是方差和协方差
协方差
在统计学上,协方差用来刻画两个随机变量之间的相关性,反映的是变量之间的二阶统计特性。考虑两个随机变量 X i X_i Xi和 X j X_j Xj,它们的协方差定义为
c o v ( X i , X j ) = E [ ( X i − E ( X i ) ) ( X j − E ( X j ) ) ] cov(X_i, X_j) = E[(X_i - E(X_i))(X_j - E(X_j))] cov(Xi,Xj)=E[(Xi−E(Xi))(Xj−E(Xj))]
tips:独立,不相关与协方差为零三者的关系
只讨论离散型随机变量的情形。
独立:随机变量 ξ , η \xi ,\eta ξ,η独立是指对于任意的常数a,b,都有 P ( ξ = a , η = b ) = P ( ξ = a ) ⋅ P ( η = b ) P(\xi = a, \eta = b) = P(\xi = a) \cdot P(\eta = b) P(ξ=a,η=b)=P(ξ=a)⋅P(η=b).
相关性,相关系数 ρ ξ η = c o v ( ξ , η ) v a r ( ξ ) v a r ( η ) \rho _{\xi \eta } = \frac {cov(\xi, \eta)}{\sqrt{var(\xi)} \sqrt{var(\eta)}} ρξη=var(ξ)var(η)cov(ξ,η)
相关系数其实是“线性相关系数”
相关系数和协方差在描述相关性方面是等价的,但独立与相关性的关系是:**独立=>不相关**
协方差矩阵:
假设有m个变量,特征维度为2, a 1 a_1 a1表示变量1的a特征。那么构成的数据集矩阵为:
X = ( a 1 a 2 . . . a m b 1 b 2 . . . b m ) X=\begin{pmatrix} a_1 & a_2 &...& a_m\\ b_1 & b_2 &...&b_m \end{pmatrix} X=(a1b1a2b2......ambm)
再假设它们的均值都是0,对于有两个均值为0的m维向量组成的向量组, 1 m X X T = ( 1 m ∑ i = 1 m a i 2 1 m ∑ i = 1 m a i b i 1 m ∑ i = 1 m a i b i 1 m ∑ i = 1 m b i 2 ) \frac 1mXX^T=\begin{pmatrix} \frac 1m \sum_{i=1}^m a_i^2 & \frac 1m \sum_{i=1}^m a_ib_i\\ \frac 1m \sum_{i=1}^m a_ib_i & \frac 1m \sum_{i=1}^m b_i^2 \end{pmatrix} m1XXT=(m1∑i=1mai2m1∑i=1maibim1∑i=1maibim1∑i=1mbi2)
可以发现对角线上的元素是两个字段的方差,其他元素是两个字段的协方差,两者都被统一到了一个矩阵——协方差矩阵中。
回顾一下前面所说的PCA算法的目标:方差max,协方差min!!
要达到PCA降维目的,等价于将协方差矩阵对角化:即除对角线外的其他元素化为0,并且在对角线上将元素按大小从上到下排列,这样我们就达到了优化目的。
设原始数据矩阵X对应的协方差矩阵为C,而P是一组基按行组成的矩阵,设Y=PX,则Y为X对P做基变换后的数据。设Y的协方差矩阵为D,我们推导一下D与C的关系: D = 1 m Y Y T = 1 m ( P X ) ( P X ) T = 1 m P X X T P T = P ( 1 m X X T ) P T = P C P T D = \frac 1m YY^T = \frac 1m (PX)(PX)^T = \frac 1m PXX^TP^T = P(\frac 1m XX^T)P^T = PCP^T D=m1YYT=m1(PX)(PX)T=m1PXXTPT=P(m1XXT)PT=PCPT
解释:想让原始数据集X =>pca成数据集Y,使得Y的协方差矩阵是个对角矩阵。
有上述推导可得,若有矩阵P能使X的协方差矩阵对角化,则P就是我们要找的PCA变换。
优化目标变成了寻找一个矩阵 P P P,满足 P C P T PCP^T PCPT是一个对角矩阵,并且对角元素按从大到小依次排列,那么 P P P的前 K K K行就是要寻找的基,用 P P P的前 K K K行组成的矩阵乘以 X X X就使得 X X X从 N N N维降到了 K K K维并满足上述优化条件。
矩阵对角化
首先,原始数据矩阵X的协方差矩阵C是一个实对称矩阵,它有特殊的数学性质:
- 实对称矩阵不同特征值对应的特征向量必然正交。
- 设特征值 λ \lambda λ重数为r,则必然存在r个线性无关的特征向量对应于 λ \lambda λ,因此可以将这r个特征向量单位正交化。
一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量,设这n个特征向量为 e 1 , e 2 , . . . , e n e_1, e_2, ..., e_n e1,e2,...,en,我们将其按列组成矩阵: E = ( e 1 e 2 . . . e n ) E = (e_1 \ e_2 \ ... \ e_n) E=(e1 e2 ... en)
则对协方差矩阵C有如下结论:
E T C E = Λ = ( λ 1 λ 2 . . . λ n ) E^TCE = \Lambda = \begin{pmatrix} \lambda_1 & & & \\ &\lambda_2 & & \\ & &... & \\ & & &\lambda_n \end{pmatrix} ETCE=Λ=⎝⎜⎜⎛λ1λ2...λn⎠⎟⎟⎞这里不懂的朋友可以查阅线性代数相关书籍。
P = E T P = E^T P=ET
P是协方差矩阵的特征向量单位化后按行排列出的矩阵,其中每一行都是C的一个特征向量。如果设P按照中特征值的从大到小,将特征向量从上到下排列,则用P的前K行组成的矩阵乘以原始数据矩阵X,就得到了我们需要的降维后的数据矩阵Y。
在解释一下,特征值 λ \lambda λ为什么要从大到小排列,为什么要选较大的 λ \lambda λ???
因为我们协方差矩阵的对角线元素是方差,我们想要找方差交大的特征维度,所以要选择较大的对角线元素。
而对角矩阵 Λ \Lambda Λ虽然是C经过线性变化后的矩阵,但它在对角线上元素的大小关系没变,特征维度 i i i对应的特征值 λ i \lambda_i λi越大,该维度上数据的方差越大。
另一种解释思路
该思路基于拉格朗日问题的求解方法。
回到一开始, z = w T x z=w^Tx z=wTx。其中,最主要的成分是这样的 w 1 w_1 w1,样本投影到 w 1 w_1 w1上之后最分散,使得样本点之间的差别变得最明显。为了得到唯一解且是该方向成为最重要的因素,我们要求 ∣ ∣ w 1 ∣ ∣ = 1 ||w_1|| = 1 ∣∣w1∣∣=1. 如果 z 1 = w 1 T x z_1={w_1}^Tx z1=w1Tx且 C o v ( x ) = ∑ Cov(x)=\sum Cov(x)=∑,则
V a r ( z 1 ) = E [ ( w T x − w T μ ) 2 ] = w 1 t ∑ w 1 Var(z_1) =E[(w^Tx - w^T\mu)^2] = {w_1}^t\sum w_1 Var(z1)=E[(wTx−wTμ)2]=w1t∑w1
寻找 w 1 w_1 w1,使得 w 1 w_1 w1在约束下最大化。将这写成拉格朗日问题,则有:
max w 1 w 1 T ∑ w 1 − α ( w 1 T w 1 − 1 ) \max_{w_1}{w_1}^T\sum w_1 - \alpha(w_1^Tw_1 - 1) w1maxw1T∑w1−α(w1Tw1−1)
关于 w 1 w_1 w1求导并让它等于0,有:
2 ∑ w 1 − 2 α w 1 = 0 2\sum w_1 - 2\alpha w_1 = 0 2∑w1−2αw1=0
因此, ∑ w 1 = α w 1 \sum w_1 = \alpha w_1 ∑w1=αw1
如果 w 1 w_1 w1是协方差矩阵 ∑ \sum ∑的特征向量,a是对应的特征值,则上式成立。因为我们想最大化
V a r ( z 1 ) = w 1 T ∑ w 1 = α w 1 T w 1 = α Var(z_1) = w_1^T \sum w_1 = \alpha w_1^Tw_1 = \alpha Var(z1)=w1T∑w1=αw1Tw1=α
所以为了方差最大,我们选择具有最大特征值的特征向量。因此,主成分是输入样本的协方差矩阵的具有最大特征值 λ 1 = α \lambda_1 = \alpha λ1=α的特征向量。
第二个主成分 w 2 w_2 w2也应该是最大化方差,具有单位长度,并且与 w 1 w_1 w1正交。后一个要求是使得投影后 z 2 = w 2 T x z_2=w_2^Tx z2=w2Tx与 z 1 z_1 z1不相关。对于第二个主成分,有
max w 2 w 2 T ∑ w 2 − α ( w 2 T w 2 − 1 ) − β ( w 2 T w 1 − 0 ) \max_{w_2} w_2^T \sum w_2 - \alpha(w_2^Tw_2 - 1) - \beta(w_2^Tw_1 - 0) w2maxw2T∑w2−α(w2Tw2−1)−β(w2Tw1−0)
最后,该式简化为 ∑ w 2 = α w 2 \sum w_2 = \alpha w_2 ∑w2=αw2,这表明 w 2 w_2 w2应该是 ∑ \sum ∑的具有第二大特征值 λ 2 = α \lambda_2=\alpha λ2=α的特征向量。类次的,我们可以证明其他维被具有递减特征值的特征向量给出。
算法及实例
PCA算法
总结一下PCA的算法步骤:
设有n条m维数据。
- 将原始数据按列组成m行n列矩阵X
- 将X的每一行(代表一个属性字段)进行零均值化
- 求出协方差矩阵 C = 1 m X X T C = \frac 1m XX^T C=m1XXT
- 求出协方差矩阵的特征值及对应的特征向量
- 将特征相浪按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
- Y = P X Y = PX Y=PX即为降维到k维后的数据
关于PCA的python实现代码可以参考这里,不过ipynb文件可能在github上刷不出来,建议下载下来用jupyter notebook打开。
实例
原始数据集矩阵X:
( 1 1 2 4 2 1 3 3 4 4 ) \begin{pmatrix} 1 & 1 & 2 & 4 & 2 \\ 1 & 3 & 3 & 4 & 4 \end{pmatrix} (1113234424)
求均值后:
( − 1 − 1 0 2 0 − 2 0 0 1 1 ) \begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{pmatrix} (−1−2−10002101)
再求协方差矩阵
C = 1 5 ( − 1 − 1 0 2 0 − 2 0 0 1 1 ) ⋅ ( − 1 − 2 − 1 0 0 0 2 1 0 1 ) = ( 6 5 4 5 4 5 6 5 ) C = \frac 15 \begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{pmatrix} \cdot \begin{pmatrix} -1 &-2 \\ -1 &0 \\ 0 &0 \\ 2 &1 \\ 0 &1 \end{pmatrix} = \begin{pmatrix} \frac65 &\frac45 \\ \frac45 &\frac65 \end{pmatrix} C=51(−1−2−10002101)⋅⎝⎜⎜⎜⎜⎛−1−1020−20011⎠⎟⎟⎟⎟⎞=(56545456)
特征值:
λ 1 = 2 , λ 2 = 2 5 \lambda_1 = 2, \lambda_2 = \frac 25 λ1=2,λ2=52
对应的特征向量:
c 1 ( 1 2 1 2 ) , c 1 ( − 1 2 1 2 ) c1\begin{pmatrix} \frac 1{\sqrt 2}\\ \frac 1{\sqrt 2} \end{pmatrix}, c1\begin{pmatrix} -\frac 1{\sqrt 2}\\ \frac 1{\sqrt 2} \end{pmatrix} c1(2121),c1(−2121)
标准化(其实不标准化也一样,只是稍显不专业)
P = ( 1 2 1 2 − 1 2 1 2 ) P = \begin{pmatrix} \frac 1{\sqrt 2} &\frac 1{\sqrt 2} \\ -\frac 1{\sqrt 2} &\frac 1{\sqrt 2} \end{pmatrix} P=(21−212121)
选择较大特征值对应的特征向量:
( 1 2 1 2 ) \begin{pmatrix} \frac 1{\sqrt 2} &\frac 1{\sqrt 2} \end{pmatrix} (2121)
执行PCA变换:Y=PX,得到的Y就是PCA降维后的值数据集矩阵:
Y = ( 1 2 1 2 ) ⋅ ( − 1 − 1 0 2 0 − 2 0 0 1 1 ) = ( − 3 2 − 1 2 0 3 2 1 2 ) Y = \begin{pmatrix} \frac 1{\sqrt 2} &\frac 1{\sqrt 2} \end{pmatrix} \cdot \begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{pmatrix} = \begin{pmatrix} -\frac 3 {\sqrt 2} & -\frac 1 {\sqrt 2} & 0 & \frac 3 {\sqrt 2} & \frac 1 {\sqrt 2}\end{pmatrix} Y=(2121)⋅(−1−2−10002101)=(−23−2102321)
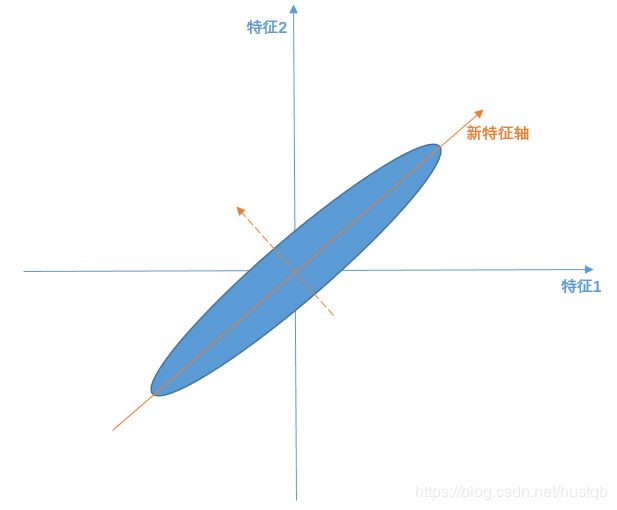
降维过程的示意图
进一步讨论
根据上面对PCA的数学原理的解释,我们可以了解到一些PCA的能力和限制。PCA本质上是将方差最大的方向作为主要特征,并且在各个正交方向上将数据“离相关”,也就是让它们在不同正交方向上没有相关性。
因此,PCA也存在一些限制,例如它可以很好的解除线性相关,但是对于高阶相关性就没有办法了,对于存在高阶相关性的数据,可以考虑Kernel PCA,通过Kernel函数将非线性相关转为线性相关,关于这点就不展开讨论了。另外,PCA假设数据各主特征是分布在正交方向上,如果在非正交方向上存在几个方差较大的方向,PCA的效果就大打折扣了。
最后需要说明的是,PCA是一种无参数技术,也就是说面对同样的数据,如果不考虑清洗,谁来做结果都一样,没有主观参数的介入,所以PCA便于通用实现,但是本身无法个性化的优化。