为什么用交叉熵做损失函数

博客已迁移至知乎 本文地址：https://zhuanlan.zhihu.com/p/70804197

前言

在处理分类问题的神经网络模型中，很多都使用交叉熵 (cross entropy) 做损失函数。
这篇文章详细地介绍了交叉熵的由来、为什么使用交叉熵，以及它解决了什么问题，最后介绍了交叉熵损失函数的应用场景。

---

要讲交叉熵就要从最基本的信息熵说起。

1.信息熵

信息熵是消除不确定性所需信息量的度量。（多看几遍这句话）

信息熵就是信息的不确定程度，信息熵越小，信息越确定。

$$信息熵=\sum _{x=1}^n(信息x发生的概率\times 验证信息x需要的信息量)$$

(因为事件都有个概率分布，这里我们只考虑离散分布)

举个列子，比如说：今年中国取消高考了，这句话我们很不确定(甚至心里还觉得这TM是扯淡)，那我们就要去查证了，这样就需要很多信息量(去查证)；反之如果说今年正常高考，大家回想：这很正常啊，不怎么需要查证，这样需要的信息量就很小。从这里我们可以学到：根据信息的真实分布，我们能够找到一个最优策略，以最小的代价消除系统的不确定性，即最小信息熵。

简而言之，概率越低，需要越多的信息去验证，所以验证真假需要的信息量和概率成反比。我们需要用数学表达式把它描述出来，推导：

考虑一个离散的随机变量 $x$，已知信息的量度依赖于概率分布 $p(x)$，因此我们想要寻找一个函数 $I(x)$，它是概率$p(x)$的单调函数，表示信息量。
怎么寻找呢？如果我们有两个不相关的事件 $x$ 和 $y$，那么观察两个事件同时发生时获得的信息量应该等于观察到事件各自发生时获得的信息之和，即：
$$I(x,y)=I(x)+I(y)$$

因为两个事件是独立不相关的，因此
$$p(x,y)=p(x)p(y)$$

根据这两个关系，很容易看出 $I(x)$一定与 $P(x)$ 的对数有关。
由对数的运算法则可知：
$$lo{g}_a(p(x)p(y))=lo{g}_{a}p(x)+lo{g}_{a}p(y)$$

因此，我们有
$$I(x)=-log(p(x))$$

其中负号是用来保证信息量是正数或者零。而 $log$ 函数基的选择是任意的（信息论中基常常选择为2，因此信息的单位为比特bits；而机器学习中基常常选择为自然常数，因此单位常常被称为奈特nats）。$I(x)$ 也被称为随机变量 x 的自信息 (self-information)，描述的是随机变量的某个事件发生所带来的信息量。

以上推导借鉴了这篇博客。

信息熵即所有信息量的期望：
$$H(X)=-\sum _{x}p(x)log(p(x))=-\sum _{i=1}^{n}p(x_i)log(p(x_i))$$

其中n为事件的所有可能性。

---

2.相对熵(KL散度)

相对熵又称KL散度，如果对于同一个随机变量$x$有两个单独的概率分布$p(x)$和 $q(x)$，可以使用相对熵来衡量这两个分布的差异。
$$D_{KL}(p||q)=\sum _{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)})$$

注：$D_{KL}$越小，表示p(x)和q(x)的分布越近。

---

3.交叉熵

交叉熵公式：
$$H(p,q)=-\sum _{i=1}^{n}p(x_i)log(q(x_i))$$

相对熵的推导：
$$\begin{array}{l}{D}_{KL}(p||q)\\ \\ ={\sum }_{i=1}^{n}p(x_i)log(p(x_i))-{\sum }_{i=1}^{n}p(x_i)log(q(x_i))\\ \\ =-H(X)+[-{\sum }_{i=1}^{n}p(x_i)log(q(x_i))]\\ \\ =[-{\sum }_{i=1}^{n}p(x_i)log(q(x_i))]-H(X)\end{array}$$

在机器学习中，往往用$p(x)$用来描述真实分布，$q(x)$用来描述模型预测的分布。

计算损失，理应使用相对熵来计算概率分布的差异，然而由相对熵推导出的结果看：

$$相对熵=交叉熵-信息熵$$

由于信息熵描述的是消除 $p$ (即真实分布) 的不确定性所需信息量的度量，所以其值应该是最小的、固定的。那么：优化减小相对熵也就是优化交叉熵，所以在机器学习中使用交叉熵就可以了。

---

4.为什么使用交叉熵

在机器学习中，我们希望模型在训练数据上学到的预测数据分布与真实数据分布越相近越好，上面讲过了，用相对熵，但是为了简便计算使用交叉熵就可以了。

注意：此处真实数据分布指的就是训练数据的分布(标注)。

交叉熵损失函数：

$$L=-[ylog\hat{y}+(1-y)log(1-\hat{y})]$$

交叉熵损失函数一般用来代替均方差损失函数与sigmoid激活函数组合。
sigmoid激活函数表达式：
$$\sigma (z)=\frac{1}{1+e^{-z}}$$

下面是sigmoid函数及其导数的图像：
[外链图片转存失败(img-zGeLUZMx-1565158338849)(https://ws1.sinaimg.cn/large/e3bfcf62ly1fy1heq9aroj20sh0gymy7.jpg =800x)]

从图中可以看出，对于sigmoid函数，当$x$的取值越大或越小，函数曲线变得越平缓，意味着导数$\sigma \prime (x)$越趋近于0。

以单个样本的一次梯度下降为例：

$$z=wx+b$$

$$\hat{y}=a=\sigma (z)$$

$$L_1(y,a)=\frac{1}{2}(y-a{)}^2$$

$$L_2(y,a)=-(ylog(a)+(1-y)log(1-a))$$

前两个公式公式分别是前向传播的线性和非线性部分，第三个公式公式是均方差损失函数，第四个公式是交叉熵损失函数。梯度下降的目的，直白地说：是减小真实值和预测值的距离，而损失函数用来度量真实值和预测值之间距离，所以梯度下降目的也就是减小损失函数的值。怎么减小损失函数的值呢？变量只有$w$和$b$，所以我们要做的就是不断修改$w$和$b$的值以使损失函数越来越小。(这里例子只有一步，只修改一次)

$w$和$b$的更新：$参数=参数-学习率\times 损失函数对参数的偏导$：

$$w=w-\alpha \frac{\partial L(y,a)}{\partial w}$$

$$b=b-\alpha \frac{\partial L(y,a)}{\partial w}$$

其中$\alpha$ 表示学习率，用来控制步长，即向下走一步的长度

为什么要这样更新参数呢，讲完下面的关键点我们会解释一下。

关键点来了，为什么用交叉熵而不是均方差呢？

均方差对参数的偏导：

$$\frac{\partial L_1(y,a)}{\partial w}=-|y-\sigma (z)|{\sigma }^{\prime }(z)x$$

$$\frac{\partial L_1(y,a)}{\partial b}=-|y-\sigma (z)|{\sigma }^{\prime }(z)$$

交叉熵对参数的偏导：

$$\frac{\partial L_2(y,a)}{\partial w}=x[\sigma (z)-y]$$

$$\frac{\partial L_2(y,a)}{\partial w}=\sigma (z)-y$$

注：为了简洁，以上公式中用 $z$ 代替了 $wx+b$

从以上公式可以看出：均方差对参数的偏导的结果都乘了sigmoid的导数${\sigma }^{\prime }(z)x$，而之前看图发现sigmoid导数在其变量值很大或很小时趋近于0，所以偏导数很有可能接近于0。
由参数更新公式： $参数=参数-学习率\times 损失函数对参数的偏导$
可知，偏导很小时，参数更新速度会变得很慢，而当偏导接近于0时，参数几乎就不更新了。

反观交叉熵对参数的偏导就没有sigmoid导数，所以不存在这个问题。这就是选择交叉熵而不选择均方差的原因。

---

梯度下降的原理，为什么要这样更新参数

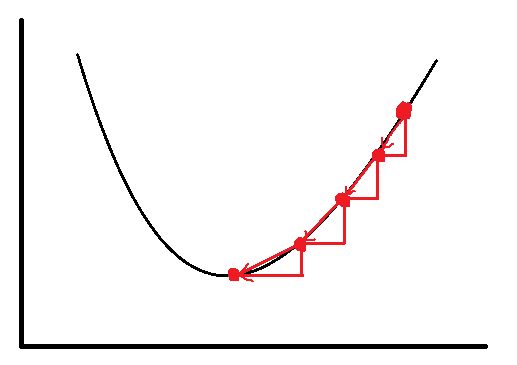
借用吴恩达深度学习课上的图：

在这个图中，横轴表示参数w和b，在实践中，w可以是更高的维度，但是为了更好地绘图，我们定义w和b都是单一实数，损失函数$J(w,b)$是在水平轴和上的曲面，因此曲面的高度就是$J(w,b)$在某一点的函数值。我们所做的就是找到使得损失函数$J(w,b)$函数值为最小值时，对应的参数w和b。
两个参数不太好说明，我们把它简化成一个参数来讲，假设损失函数只有$w$一个参数：

图画的丑，能说明意思就行，曲线是损失函数，参数w为横坐标，红色的点记录参数$w$的每次更新(这里例子只有一步，只更新一次)。
损失函数对$w$的偏导$\frac{\partial L_1(y,a)}{\partial w}$相当于曲线的斜率，$w=w-\alpha \frac{\partial L(y,a)}{\partial w}$，会使红点像曲线下端移动，这样就减小了损失函数。多个参数也是同样的道理。

---

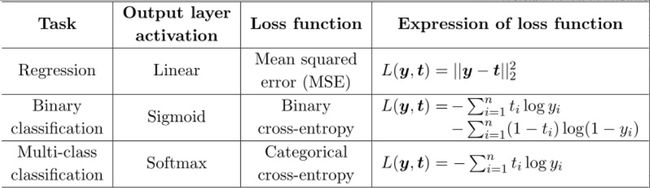
5.使用场景

下面是知乎上看到的一张图，图中写得很清楚了。

CSDN图片显示不正常，博客已迁移至知乎：https://zhuanlan.zhihu.com/p/70804197

---

References：

[1] 详解机器学习中的熵、条件熵、相对熵和交叉熵
[2] 吴恩达深度学习课程
[3] 知乎：为什么交叉熵（cross-entropy）可以用于计算代价？
[4] 使用ReLU作为激活函数还有必要用交叉熵计算损失函数吗？