算法图解第八章笔记与习题(贪婪算法)
算法图解第八章笔记与习题(贪婪算法)
文章目录
- 算法图解第八章笔记与习题(贪婪算法)
- 8.1 贪婪算法
- 8.2 集合覆盖问题
- 8.3 NP完全问题
- 8.3.1 旅行商问题:
- 8.3.2 如何识别NP完全问题
- 8.4 小结
- 练习
- 习题8.1:
- 习题8.2:
- 习题8.3-5题干:
- 习题8.3:
- 习题8.4:
- 习题8.5:
- 习题8.6:
- 习题8.7:
- 习题8.8:
算法图解pdf百度云链接,提取码:jttg
8.1 贪婪算法
贪婪算法:对于一个问题,根据问题要求的目标,每步都选择局部最优解。在某些特定的情况下,贪婪算法能够得到最优解,但通常只能能够得到一个接近最优解的解。
举例:从十个数中选择五个使其和最大1,2,3,4,5,6,7,8,9,10。
根据问题要求的目标(和最大),每步都选择局部最优解(从未被选择的数中选择最大的那个数)。对于这个简单的情况来说,贪婪算法将得到最优解10+9+8+7+6=40。但对于更复杂的情况来说,通常会得到一个接近最优解的解。
8.2 集合覆盖问题
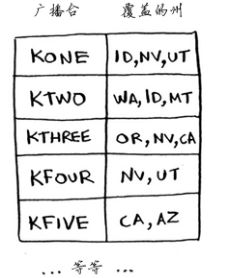
假设现在有个广播节目,要让全美国50个州的听众都收听得到,为此,需要决定在哪些广播台播出。在每个广播台播出都需要支付费用,因此必须在尽可能少的广播台播出。现有广播台名单如下:
每个广播台都覆盖特定的区域,不同广播台的覆盖区域可能重叠。
那么找出覆盖全美50个州的最小广播台合集呢?下面是解决步骤:
- 列出每个可能的广播台集合,这被称为幂集(power set)。可能的子集有 2 n 2^n 2n个。
- 在这些集合中,选出覆盖全美50个州的最小集合。
这样做固然能找到最优解,但其时间复杂度为 O ( 2 n ) O(2^n) O(2n),其中n为广播台数量。在这种情况下,我们可以使用贪婪算法来解决这个问题。步骤如下:
- 选出这样一个广播台,即它覆盖了最多未覆盖的州。即便这个广播台覆盖了一些已覆盖的州(就是重复覆盖),也没有关系。
- 重复第一步,直到覆盖了所有的州。
这是一种近似算法(approximation algorithm)。在获得精确解需要的时间太长时,可以考虑使用近似算法。判断近似算法优劣的标准如下:
- 速度有多快;
- 得到的近似解与最优解的接近程度。
因此贪婪算法是一个不错的选择,它们不仅简单,而且通常运行速度很快。在本例中,贪婪算法的运行时间为 O ( n 2 ) O(n^2) O(n2),其中n为广播台数量。
代码如下:
# 创建一个列表,其中包含要覆盖的州
states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"]) # 传入一个数组,被转换为集合
stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])
final_stations = set() # 使用一个集合来存储最终选择的广播台
while states_needed:
best_station = None # 将覆盖了最多的未覆盖州的广播台存储进去
states_covered = set() # 一个集合,包含该广播台覆盖的所有未覆盖的州
for station, states in stations.items(): # 循环迭代每个广播台并确定它是否是最佳的广播台
covered = states_needed & states # 计算交集
if len(covered) > len(states_covered): # 检查该广播台的州是否比best_station多
best_station = station # 如果多,就将best_station设置为当前广播台
states_covered = covered
states_needed -= states_covered # 更新states_needed
final_stations.add(best_station) # 在for循环结束后将best_station添加到最终的广播台列表中
print(final_stations) # 打印final_stations
set(['ktwo', 'kthree', 'kone', 'kfive'])
#(算法也可以用未被覆盖的州来做比较,未被覆盖的州越少,则该广播台是局部更优的广播台。)
上述代码中,set()是一种集合,类似于列表,但相同的元素在其中出现一次,也没有索引供查找。
另外,还涉及到了数学中交集的计算&,以及集合间相见-=。具体不做详细介绍。
使用上述贪婪算法的运行时间仅为 O ( n 2 ) O(n^2) O(n2),比起遍历所有子集来获得精确解的精确算法 O ( 2 n ) O(2^n) O(2n)来说非常快。
8.3 NP完全问题
8.3.1 旅行商问题:
旅行商问题是指,旅行商需要在一次旅行中途径多个不同的城市,如何求解其最短路径。
对于 1 个城市而言,仅有 1 条可能的路径。
对于 2 个城市而言,有 2 个可能的起点X每个出发的城市1条可能的路径 = 2条可能的路径。
对于 3 个城市而言,有 3 个可能的起点X每个出发的城市2条可能的路径 = 6条可能的路径。
对于 4 个城市而言,有 4 个可能的起点X每个出发的城市6条可能的路径 = 24条可能的路径。
对于 5 个城市而言,有 5 个可能的起点X每个出发的城市24条可能的路径 = 120条可能的路径。
……
这是一个阶乘函数(factorical function),当涉及的城市越多时,可能的路径条数增加的非常快。因此当涉及的城市足够多时,根本就难以计算出旅行商问题的正确解。
NP完全问题的简单定义是,以难著称的问题,如旅行商问题和集合覆盖问题。(?)
8.3.2 如何识别NP完全问题
NP完全问题无处不在!如果能够判断出要解决的问题属于NP完全问题就好了,这样就不用去寻找完美的解决方案,而是使用近似算法即可。但要判断问题是不是NP完全问题很难,易于解决的问题和NP完全问题的差别通常很小。
但事实是没办法判断问题是不是NP完全问题,但还是有迹可循的:
- 元素较少时算法的运行速度非常快,但随着元素数量的增加,速度会变得非常慢。
- 涉及“所有组合”的问题通常是NP完全问题。
- 不能将问题分成小问题,必须考虑各种可能的情况。这可能是NP完全问题。
- 如果问题涉及序列(如旅行商问题中的城市序列)且难以解决,它可能就是NP完全问题。
- 如果问题涉及集合(如广播台集合)且难以解决,它可能就是NP完全问题。
- 如果问题可转换为集合覆盖问题或旅行商问题,那它肯定是NP完全问题。
8.4 小结
- 贪婪算法寻找局部最优解,企图以这种方式获得全局最优解。
- 对于NP完全问题,还没有找到快速解决方案。
- 面临NP完全问题时,最佳的做法是使用近似算法。
- 贪婪算法易于实现、运行速度快,是不错的近似算法。
练习
习题8.1:
- 你在一家家具公司工作,需要将家具发往全国各地,为此你需要将箱子装上卡车。每个箱子的尺寸各不相同,你需要尽可能利用每辆卡车的空间,为此你将如何选择要装上卡车的箱子呢?请设计一种贪婪算法。使用这种算法能得到最优解吗?
将剩余箱子中最大的一个装入箱子,直到将所有的箱子装入卡车为止。使用这种算法不能找到最优解。
习题8.2:
- 你要去欧洲旅行,总行程为7天。对于每个旅游胜地,你都给它分配一个价值——表示你有多想去那里看看,并估算出需要多长时间。你如何将这次旅行的价值最大化?请设计一种贪婪算法。使用这种算法能得到最优解吗?
从剩余未去过的旅游胜地中选择价值最高的,直至时间用完为止。使用这种算法不能找到最优解。
习题8.3-5题干:
- 下面各种算法是否是贪婪算法。
习题8.3:
- 快速排序。
不是。
习题8.4:
- 广度优先搜索。
是。
习题8.5:
- 狄克斯特拉算法。
是。
习题8.6:
- 有个邮递员负责给20个家庭送信,需要找出经过这20个家庭的最短路径。请问这是一 个NP完全问题吗?
是。可转化为旅行商问题。
习题8.7:
- 在一堆人中找出最大的朋友圈(即其中任何两个人都相识)是NP完全问题吗?
是。可转化为集合覆盖问题。
习题8.8:
- 你要制作美国地图,需要用不同的颜色标出相邻的州。为此,你需要确定最少需要使用多少种颜色,才能确保任何两个相邻州的颜色都不同。请问这是NP完全问题吗?
不是。(图着色问题,是NP完全问题。)