巴尔加瓦算法图解：K最近邻算法

巴尔加瓦算法图解：K最近邻算法

本章内容
❑ 学习使用K最近邻算法创建分类系统。❑ 学习特征抽取。❑ 学习回归，即预测数值，如明天的股价或用户对某部电影的喜欢程度。❑ 学习K最近邻算法的应用案例和局限性。

判断水果

判断这个水果是橙子还是柚子呢？一种办法是看它的邻居。来看看离它最近的三个邻居。在这三个邻居中，橙子比柚子多，因此这个水果很可能是橙子。祝贺你，你刚才就是使用K最近邻(k-nearest neighbours,KNN)算法进行了分类！

顺便说一句，其实并非一定要选择3个最近的邻居，也可选择2个、10个或10000个。这就是这种算法名为K最近邻而不是5最近邻的原因！

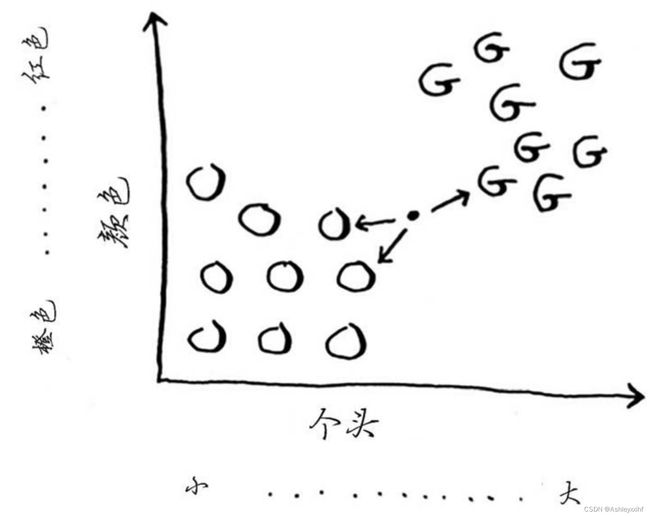
创建推荐系统

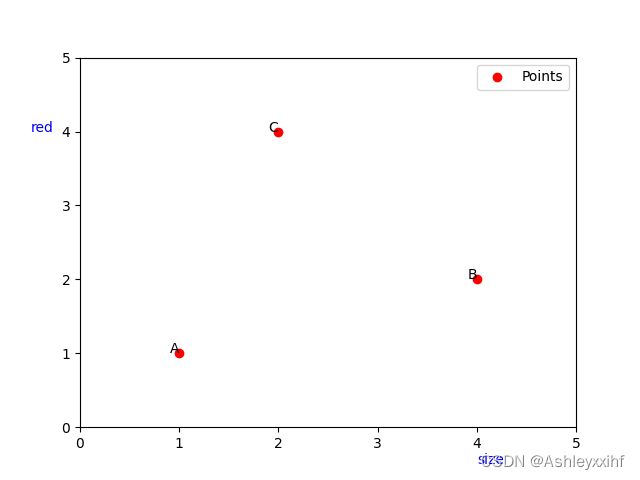
1. 判断相似程度

例子：比较个头和颜色，绘制坐标轴。

import matplotlib.pyplot as plt

# 设置坐标轴范围
plt.xlim(0, 5)
plt.ylim(0, 5)

# 绘制坐标轴
plt.axhline(0, color='black',linewidth=0)
plt.axvline(0, color='black',linewidth=0)

# 绘制横坐标
plt.text(4, -0.5, 'size',color='blue')

# 绘制纵坐标（颜色为蓝色）
plt.text(-0.5, 4, 'red', color='blue')

# 绘制点 A、B、C
plt.scatter([1, 4, 2], [1, 2, 4], c='red', marker='o', label='Points')
plt.text(1, 1, 'A', ha='right') #右边对齐
plt.text(4, 2, 'B', ha='right')
plt.text(2, 4, 'C', ha='right')

# 显示图例
plt.legend()

# 显示图形
plt.show()

再用毕达哥拉斯公式
$$c=\sqrt{a^2+b^2}$$

练习

1.在Netflix示例中，你使用距离公式计算两位用户的距离，但给电影打分时，每位用户的标准并不都相同。假设你有两位用户——Yogi和Pinky，他们欣赏电影的品味相同，但Yogi给喜欢的电影都打5分，而Pinky更挑剔，只给特别好的电影打5分。他们的品味一致，但根据距离算法，他们并非邻居。如何将这种评分方式的差异考虑进来呢？

• 评分归一化： 将用户的评分归一到一个标准范围内，例如0到1之间。这有助于消除由于评分尺度不同而导致的偏差。
• 用户偏好建模： 考虑到不同用户的评分习惯，推荐系统可以采用更复杂的模型，例如考虑到用户的平均评分水平，以更好地捕捉他们的个性化喜好。
• 隐式反馈： 有时，用户并不直接给电影打分，而是通过观看时间、点击次数等隐式行为表达他们的喜好。这种隐式反馈也可以用于个性化推荐。
• 深度学习模型： 使用深度学习技术，能够更好地捕捉用户和电影之间的复杂关系，从而更精准地进行推荐。

2.假设Netflix指定了一组意见领袖。例如，Quentin Tarantino和WesAnderson就是Netflix的意见领袖，因此他们的评分比普通用户更重要。请问你该如何修改推荐系统，使其偏重于意见领袖的评分呢？

• 给意见领袖的评分赋予更高的权重。例如，如果一部电影被Quentin Tarantino评分为5分，可以将其权重乘以一个调整系数，使其对整体推荐的影响更大。

回归（预测结果）

这就是回归(regression)。你将使用KNN来做两项基本工作——分类和回归：❑ 分类就是编组；❑ 回归就是预测结果（如一个数字）。
找出最近的邻居，进行平均数计算。

回归分析是一种统计学方法，用于研究两个或多个变量之间的关系。主要目的是建立一个数学模型，描述一个或多个自变量如何影响因变量。在回归分析中，我们通常使用已知数据来拟合模型，并利用这个模型来进行预测或理解变量之间的关系。

关键概念：

1. 因变量（Dependent Variable）： 需要解释或预测的变量，通常用 (Y) 表示。

2. 自变量（Independent Variable）： 用来解释或预测因变量的变量，通常用 (X) 表示。可以有一个或多个自变量。

3. 回归方程（Regression Equation）： 描述了自变量和因变量之间关系的数学公式。一般形式为 $Y=f(X)+ϵ$，其中 $ϵ$ 是误差项。

4. 回归系数$\beta$（Regression Coefficients）： 描述自变量对因变量影响的系数。回归方程中的参数就是这些系数。

5. 残差（Residuals）： 观测值与回归方程预测值之间的差异，即残差。残差用于评估模型的拟合程度。

回归分析主要分为两类：

1. 简单线性回归（Simple Linear Regression）： 当只有一个自变量时使用。回归方程的形式为 $Y={\beta }_0+{\beta }_{1}X+ϵ$

2. 多元线性回归（Multiple Linear Regression）： 当有两个或多个自变量时使用。回归方程的形式为 $Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\dots +{\beta }_k{X}_k+ϵ$

回归分析可以用于预测、解释变量之间的关系、评估因变量对自变量的敏感度等。在实际应用中，回归分析广泛用于经济学、生物统计学、社会科学、工程等领域。

机器学习

1. OCR指的是光学字符识别(optical character recognition)，这意味着你可拍摄印刷页面的照片，计算机将自动识别出其中的文字。
   使用KNN：(1)浏览大量的数字图像，将这些数字的特征提取出来。(2)遇到新图像时，你提取该图像的特征，再找出它最近的邻居都是谁！这与前面判断水果是橙子还是柚子时一样。一般而言，OCR算法提取线段、点和曲线等特征。
2. 创建垃圾邮件过滤器
   假设你收到一封主题为“collect your million dollars now!”的邮件，这是垃圾邮件吗？你可研究这个句子中的每个单词，看看它在垃圾邮件中出现的概率是多少。例如，使用这个非常简单的模型时，发现只有单词million在垃圾邮件中出现过。朴素贝叶斯分类器能计算出邮件为垃圾邮件的概率，其应用领域与KNN相似。
3. 预测股票市场（不太可能）
   使用机器学习来预测股票市场的涨跌真的很难。对于股票市场，如何挑选合适的特征呢？股票昨天涨了，今天也会涨，这样的特征合适吗？又或者每年五月份股票市场都以绿盘报收，这样的预测可行吗？在根据以往的数据来预测未来方面，没有万无一失的方法。未来很难预测，由于涉及的变数太多，这几乎是不可能完成的任务。

总结

但愿通过阅读本章，你对KNN和机器学习的各种用途能有大致的认识！机器学习是个很有趣的领域，只要下定决心，你就能很深入地了解它。❑ KNN用于分类和回归，需要考虑最近的邻居。❑ 分类就是编组。❑ 回归就是预测结果（如数字）。❑ 特征抽取意味着将物品（如水果或用户）转换为一系列可比较的数字。❑ 能否挑选合适的特征事关KNN算法的成败。