算法精解-C语言描述 递归和尾递归 (图解+实例)
递归是一种强大的方法,它允许一个对象以其自身更小的形式来定义自己。
让我们来观察一下自然界中出现的递归现象:蕨类植物的叶子,每片叶子叶脉中的小分支都是整片叶子的较小缩影;又或者两个反光的物体,相互映射对方渐远的影像。这样的例子使我们明白,尽管大自然的力量是强大的,在许多方面它那种出乎意料的简洁更让我们觉得优美。同样的道理也可以用在递归算法上,从很多方面来说递归算法都是简洁而优美的,而且非常强大。
在计算机科学领域中,递归是通过函数来实现的。递归函数是一种可以调用自身的函数。
基本递归
假设我们想计算整数n的阶乘。n的阶乘可能写作n!,其结果是1~n之间的各数之积。比如,4!=4 x 3 x 2 x 1。一种方法是循环遍历其中的每一个数,然后与它之前的数相乘作为结果再参与下一次计算。这种方法称为迭代法,可以正式定义为:
n! = n(n-1)(n-2)...(1)
看待这个问题的另一种方式是将n!定义为更小的阶乘形式。我们将n!定义为n-1阶乘的n倍。再把(n-1)!定义为n-1倍的(n-2)!,(n-2)!看作(n-2)倍的(n-3)!,一直到n=1时,我们就计算完了。这就是递归的方式,可以正式定义为:
| 1 |
如果 n=0,n=1 |
|
| f(n)= |
||
| nf(n) |
如果 n>1 |
图1: 以递归的方式计算4的阶乘
上图(1)展示了利用递归计算4!的过程。它也说明了递归过程中的两个基本阶段:递推和回归。在递推阶段,每一个递归调用通过进一步调用自己来记住这次递归过程。当其中有调用满足终止条件时,递推结束。比如,在计算n!时,终止条件是当n=1和n=0,此时函数只需简单的返回1即可。每一个递归函数都必须拥有至少一个终止条件;否则递推阶段永远不会结束了。一旦递推阶段结束,处理过程就进入回归阶段,在这之前的函数调用以逆序的方式回归,直到最初调用的函数为止,此时递归过程结束。
以递归的方式计算n的阶乘的函数实现:
C函数fact的工作方式如下:它接受一个整数n作为参数,如果n小于0,该函数直接返回0,这代表一个错误。如果n等于0或1,该函数返回1,这是因为0!和1!都等于1,以上是终止递归的条件。否则,函数返回n-1的阶乘的n倍。而n-1的阶乘又会以递归的方式再次调用fact来计算,如此继续。
代码实例(1):fact.c
/*fact.c*/
#include "fact.h"
int fact(int n){
if (n<0)
return 0;
else if(n==0)
return 1;
else if(n==1)
return 1;
else
return n*f(n-1);
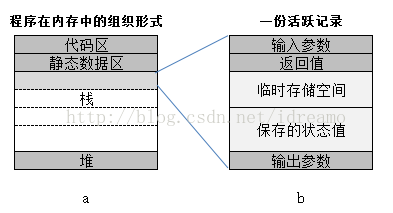
}为理解递归究竟是如何工作的,有必要先看看C语言中函数的执行方式。我们先来看看C程序在内存中的组织方式(见图2-a)。基本上,一个可执行程序由4个区域组成:代码段、静态数据区、堆与栈。代码段包含程序运行时所执行的机器指令。静态数据区包含在程序生命周期内一直持久的数据,比如全局变量和静态局部变量。堆包含程序运行时动态分配的存储空间,比如malloc分配的内存。栈包含函数调用的信息。
当C中调用了一个函数时,栈中会分配一块空间来保存与这个调用相关的信息。每一个调用都被当做是活跃的。栈上的那块存储空间称为活跃记录(见图2-b),或称为栈帧。栈帧由5个区域组成:输入参数、返回值空间、计算表达式时用到的临时存储空间、函数调用时保存的状态信息以及输出参数。输入参数是传递到活跃记录中的参数;输出参数是传递给在活跃记录中调用的函数所使用的。一个活跃记录中的输出参数就成为栈中下一个活跃记录的输入参数。函数调用所产生的活跃记录将一直存在于栈中直到这个函数调用结束。
图2: a) C程序在内存中的组织形式 b) 一份活跃记录
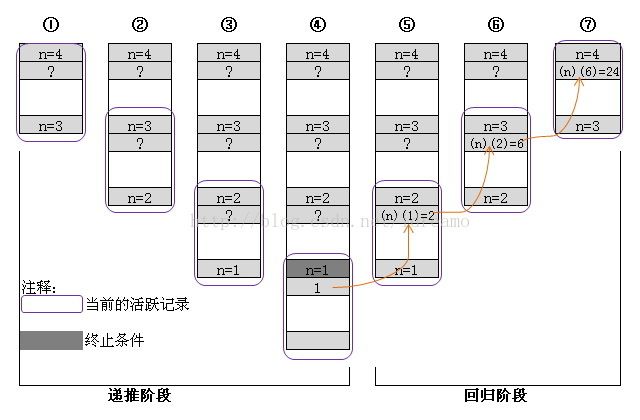
我们以示例fact.c为例,考虑一下当计算4!时栈中都发生了什么(见图3)?初始调用fact会在栈中产生一个活跃记录,输入参数n=4。由于这个调用没有满足函数的终止条件,因此fact将继续以n=3为参数递归调用。这将在栈上创建另一个活跃记录,但这次输入参数n=3。这里,n=3也是第一个活跃期中的输出参数,因为正是在第一个活跃期内调用fact产生了第二个活跃期。这个过程将一直继续,直到n的值变为1,此时满足终止条件,fact将返回1。
图3:递归计算4!时的C程序的栈
一旦n=1时的活跃期结束,n=2时的递归计算结果就是2X1=2,因而n=2时的活跃期也将结束,返回值为2。结果就是n=3时的递归计算结果表示为3X2=6,因此n=3时的活跃期结束,返回值为6。最终,当n=4时的递归计算结果将表示为6X4=24,n=4时的活跃期将结束,返回值为24。此时,函数已经从最初的调用中返回,递归过程结束。
栈是用来存储函数调用信息的绝好方案。这正是由于其后进先出的特点精确满足了函数调用和返回的顺序。然而,使用栈也有一些缺点,栈维护了每个函数调用的信息直到函数返回后才释放,这需要占用相当大的空间,尤其是在程序中使用了许多递归调用的情况下。除此之外,因为有大量的信息需要保存和恢复,因此生产和销毁活跃记录需要耗费一定的时间。如此一来,当函数调用的开销变的很大时,我们就需要考虑应该采用迭代的方案。幸运的是,我们可以使用一种称为尾递归的特殊递归方式来避免前面提到的这些缺点。
尾递归
如果一上函数中所有递归形式的调用都出现在函数的末尾,我们称这个递归函数是尾递归的。当递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分时,这个递归调用就是尾递归。
尾递归函数的特点是在回归过程中不用做任何操作。
当编译器检测到一个函数调用是尾递归的时候,它就覆盖当前的活跃记录而不是在栈中去创建一个新的。编译器可以做到这一点,因为递归调用是当前活跃期内最后一条待执行的语句,于是当这个调用返回时栈帧中并没有其他事情可做,因此也就没有保存栈帧的必要了。通过覆盖栈帧而不是在其之上重新添加一个,这样所使用的栈空间就大大缩减了,这使得实际的运行效率会变得更高。因此, 只要有可能我们就需要将递归函数写成尾递归的形式。
回忆之前对计算n!的定义:在每个活跃期计算n倍的(n-1)!的值,让n=n-1并持续这个过程直到n=1为止。这种定义不是尾递归的,因为每个活跃期的返回值都依赖于用n乘以下一个活跃期的返回值,因此每次调用产生的栈帧不得不保存在栈上直到下一个子调用的返回值确定。现在让我们考虑以尾递归的形式来定义计算n!的过程。函数可以定义成如下形式:
| a | 如果 n=0,n=1 | ||
| f(n,a)= | |||
| f(n-1,na) | 如果 n>1 |
图4:以尾递归的方式计算4!
代码实例(2):facttail.c
facttail.c接受一个整数n并以尾递归的形式计算n的阶乘。这个函数还接受一个参数a,a的初始值为1。函数使用a来维护递归层次的深度,除此之外它和fact很相似。
/*facttail.c*/
#include "facttail.h"
int facttail(int n,int a)
{
if(n<0)
return 0;
else if(n==0)
return 1;
else if(n==1)
return a;
else
return facttail(n-1,n*a);
}
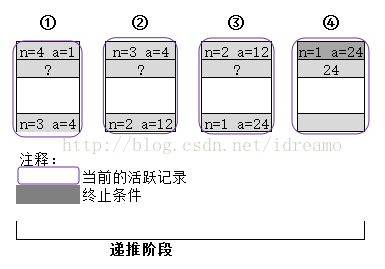
图5:以尾递归形式计算4!时栈的使用情况
递归和反向计算
下面我们来考虑一个使用递归处理反序的问题(在这类问题中使用递归比使用循环更简单)。
问题是这样的,编写一个函数将一个整数转换成二进制形式。二进制的意思是指数值以2为底数进行表示。
解决上述问题,需要使用一个算法(algorithm)。因为奇数的二进制形式的最后一位一定是1,而偶数的二进制数的最后一位是0,所以可以通过5%2得出5的进制形式中最后一位数字是1或者是0。一般来讲,对于数值n,其二进制数的最后一位是n%2,因此计算出的第一个数字恰好是需要输出的最后一位。这就需要使用一个递归函数实现。在函数中,首先在递归调用之前计算n%2的数值,然后在递归调用语句之后进行输出,这样计算出的第一个数值反而在最后一个输出。
为了得出下一个数字,需要把原数值除以2。这种计算就相当于在十进制下把小数点左移一位。如果此时得出的数值是偶数,则下一个二进制数是0;若得出的数值是奇数,则下一个二进制数是1.例如,5/2的数值是2(整数除法),所以下一位值是0。这时已经得到了数值01.重复以上计算,即使用2/2得出1,而1%2的数值是1,因此下一位数是1.这时得到的数值是101.那么何时停止这种计算呢?因为只要被2除的结果大于或等于2,那么就还需要一位二进制位进行表示,所以只有被2除的结果小于2时才停止计算。每次除以2就可以得出一位二进制位值,直到计算出最后一位为止。代码实例(3):binary.c
/*binary.c --以二进制形式输出整数*/
#include
void to_binary(unsigned long n);
int main(void)
{
unsigned long number;
printf("Enter an integer (q to quit): \n");
while(scanf("%ul",&number)==1)
{
printf("Binary equivalent: ");
to_binary(number);
putchar('\n');
printf("Enter an integer (q to quit): \n");
}
printf("Done.\n");
return 0;
}
void to_binary(unsigned long n)/*递归函数*/
{
int r ;
r = n%2;
if(n>=2)
to_binary(n/2);
putchar('0'+r); /*以字符形式输出*/
return 0;
} 示例程序中,如果r 是0,表达式‘0’+r就是字符‘0’;当r为1时,则该表达式的值为字符‘1’。得出这种结果的前提假设是字符‘1’的数值编码比字符‘0’的数值编码大1.ASCII和EBCDIC两种编码都满足上述条件。更一般的方式,你可以使用如下方法:
putchar(r ? '1' : '0' );
当然,不使用递归也能实现这个算法。但是由于本算法先计算出最后一位的数值,所以在显示结果之前必须对所有的数值进行存储。
递归的优缺点
其优点是在于为某些编程问题提供了最简单的方法,而缺点是一些递归算法会很快耗尽内存。同时,使用递归的程序难于阅读和维护。从下面的例子,可以看出递归的优缺点。
斐波纳契数列定义如下:第一个和第二个数字都是1,而后续的每个数字是前两个数字之和。例如,数列中前几个数字是1,1,2,3,5,8,13.下面我们创建一个函数,它接受一个正整数n作为参数,返回相应的斐波纳契数值。
首先,关于递归深度,递归提供了一个简单的定义。如果调用函数Fionacci(),当n为1或2时Fabonacci(n)应返回1;对于其他数值应返回Fibonacci(n-1)+Fabonacci(n-2) :
代码实例(4)
为了具体说明这个弱点,先假设调用函数Fibonacci(40)。第1级递归会创建变量n。接着它两次调用Fibonacci(),在第2级递归中又创建两个变量n。上述的两次调用中的每一次又进行了再次调用,因而在第3级调用中需要4个变量n,这时变量总数为7.因为每级调用需要的变量数是上级的两倍,所以变量的个数是以指数规律增长的!这种情况下,指数增长的变量数会占用大量内存,这就可能导致程序瘫痪。当然,以上是一个比较极端的例子,但它也表明了必须小心使用递归,尤其效率处于第一位时。
相关主题递归树:画图表能帮助我们形象地理解函数的调用顺序。递归树在形式上有所不同,展示递归计算阶乘的图1和图4都是递归树。递归树最常用在包含两个或更多个递归调用的函数中。