树状数组的原理与实现

树状数组的作用

        实际上，树状数组算是线段树的小弟角色，树状数组能解决的问题线段树一定能解决，而线段树能解决的问题树状数组却不一定能解决。两者都是在区间进行操作，但是树状数组是不如线段树厉害的。但是树状数组的有点就在于常数小，并且短小精悍，手搓的时候就几行代码快的一匹。并且lowbit函数的思想非常精妙，能从代码行中感受到美感啊（突然中二）

位运算

        树状数组涉及到大量位运算，这里不再多说，不会的同学先看看位运算、二进制的东西再学习树状数组。位运算其实并不难，并且计算机专业的话迟早要学的XD。

lowbit 函数

int lowbit(int x) return x&(-x);

        没错就是这么简单，lowbit函数可以说是树状数组的精髓了，而其作用是“二进制数从低位向高位数，第一个数字1"作为运算结果。比较难理解，看下例子好了：

lowbit(12) = 4

12的二进制为1100，从低位到高位，碰见第一个1时，截断，只取下面部分作为结果，即：100，十进制是4。

        其实就是二进制从右向左碰见第一个1时分开这个数，右边的部分转化成十进制后输出。这样，很明显我们得到的结果必定是1、2、4、8、16等数，同时在变化的过程中不断循环增大。我们只需要提供1-8的lowbit结果就可以了：

	1	2	3	4	5	6	7	8
lowbit	1	2	1	4	1	2	1	8

树状数组的原理

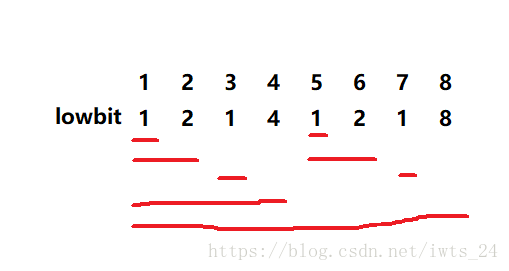
        为什么要利用lowbit函数？对树状数组有什么作用么？那么我们仍然利用上面的表格，得到这样的图：

如果把lowbit函数的值作为这个位置储存的区域和，这样就可以完美覆盖所有位置。也就是，每一个数字管理一段区间。就像线段树一样。这就是为什么我们要利用lowbit函数。

        我们在维护、使用树状数组的时候，利用累加。原来数组上利用累加的时候是i++，这样遍历一次数组时间复杂度为O(n)，我们既然可以利用lowbit，那么累加的时候将i++改为i += lowbit(i)，这样虽然我们还是在原数组上跳跃，但是可以抽象成在一个树上按顺序遍历。

树状数组的区间维护

        我们利用数组查找时候O(1)的特点，直接修改对应的数值，即：tree[index] = n。这样是最开始的一步，接下来就是维护了。我们从index开始，根据lowbit进行遍历，即：i += lowbit(i)，每次循环就将tree[i] += n，这样就保证的了树状数组的更新。

void update(int index, int n) {
    for (int i = index; i <= NUM; i += (i&-i)) {
        tree[i] += n;
    }
}

        跟线段树一样，操作是非常多变的，具体的操作有具体的写法，这里就随便写一个操作了。里面NUM这个全局变量，很明显是数据的总长度，设置成全局变量了，当然作为参数由外面传进来也是可以的。

树状数组的区间查询

        这里的区间查询很明显能感到是比线段树简单很多的，或者说查找的是前缀和。例如我们查找20，得到的是1-20的和，只能得到前缀无法得到具体的区间值。不过问题不大，我们可以通过求两次取差的方法获取区间值，例如：find(right) - find(left)。不过如果是大量的区间运算，麻烦一点写成线段树更好。

        跟更新相反，我们从index开始，利用lowbit进行递减，就可以一直减到1，就可以求出前缀和了。

int query_sum(int n) {
    int ans = 0;
    for (int i = n; i > 0; i -= (i&-i)) {
        ans += tree[i];
    }
    return ans;
}

树状数组模板

#include
#include

using namespace std;

int tree[100010];
int NUM = 100005;
/* 
注意这个NUM，应该是原数组的长度，可以设成全局变
量，在最初构造树状数组的时候手动累加。
*/

void update(int index,int n){
    for(int i = index;i < NUM;i += (i&-i)){
        tree[i] += n;
    }
}

int query_sum(int n){
    int ans = 0;
    for(int i = n;i > 0;i -= (i&-i)){
        ans += tree[i];
    }
    return ans;
}

int main() {
    
    system("pause");
    return 0;
}

hdu的树状数组模板题-1166

#include
#include
#include
#define MAX_Tot 500005

using namespace std;

int tree[50010];
int NUM = 2;

void update(int index, int n) {
    for (int i = index; i <= NUM; i += (i&-i)) {
        tree[i] += n;
    }
}

int query_sum(int n) {
    int ans = 0;
    for (int i = n; i > 0; i -= (i&-i)) {
        ans += tree[i];
    }
    return ans;
}

int main() {
    int T;
    scanf("%d", &T);
    for (int I = 1; I <= T; I++) {
        memset(tree, 0, sizeof(tree));
        cout << "Case " << I << ":" << endl;
        int N;
        int end = 0;
        scanf("%d", &N);
        NUM = N;
        for (int i = 1; i <= N; i++) {
            int num;
            scanf("%d", &num);
            update(i, num);
        }
        string com;
        int i, j;
        while (1) {
            cin >> com;
            int flag = com[0] - 'A';
            switch (flag) {
                case 0: {
                    scanf("%d%d", &i, &j);
                    update(i, j);
                }break;
                case 4: end = 1; break;
                case 16: {
                    scanf("%d%d", &i, &j);
                    cout << query_sum(j) - query_sum(i - 1) << endl;
                }break;
                case 18: {
                    scanf("%d%d", &i, &j);
                    update(i, -j);
                }break;
            }
            if (end == 1) break;
        }
    }

    system("pause");
    return 0;
}

总结

        树状数组代码量真的很少，相比于线段树，如果一些题能用树状数组还是用树状数组比较好，现场手搓的时候简单快捷不易出错。在TLE的时候利用树状数组维护可能就AC了。不过感觉用树状数组的时候还是略少吧，为了求稳，坑一点的题可能就打线段树维护了。当然菜狗就是随缘了= =毕竟大部分时间是想不到利用树状数组或者线段树去搞维护的。TLE这个设定好难啊。