深度学习基本模型浅析
深度学习基本模型浅析
-
前言
台湾李宏毅的深度学习课程说实话讲得还是比较不错的,有需要的话还是比较推荐学习,这篇也是基于它的深度学习基本结构的讲解的总结。
-
深度学习的三个步骤
深度学习首先是我们要构建一个网络,这个网络也就是我们所说的深度学习神经网络模型。深度学习一般可以归纳为下图所示的3个步骤:
第一个步骤, 神经网络模型是一个有简单函数组成的复杂的函数,通常我们设计一个神经网络模型(结构),然后用计算机从给定的训练数据中训练得到一些参数,这些参数保证我们的模型能够在测试集中达到设计预期的效果,并且具有泛化能力。
第二个步骤,根据训练数据定义一个代价函数,通过代价函数可以评估什么参数是有效的什么参数不是很有效的,模型中什么样的函数是好的什么样的函数是不好的,怎样定义一个代价函数则是根据你的具体任务和实际的训练数据来设计。
第三个步骤,根据前面两步骤的结果找出最佳的函数,例如用梯度下降的方法找出这个最佳的函数。
-
全连接层
-
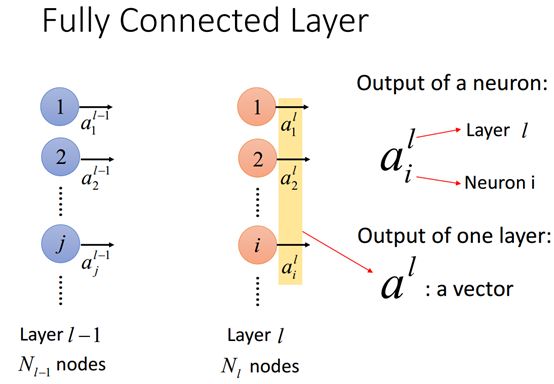
神经元向量
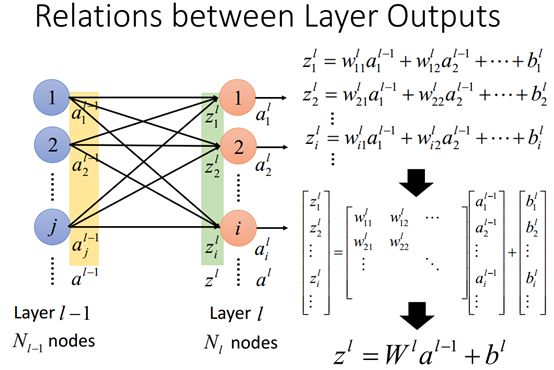
右边的输出神经元a的上标l表示第l层的神经元,i则表示在这一层上的第i个神经元,通常用一个向量方式表示所有第l层的的所有神经元。
-
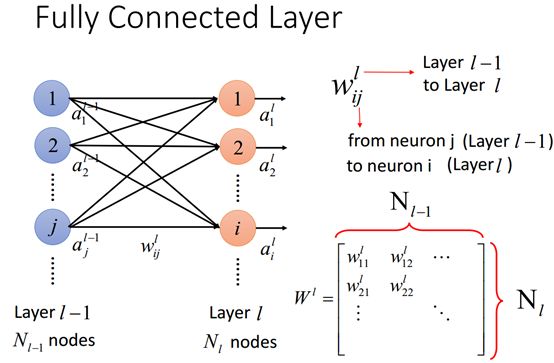
权值向量W
给这两层神经元加入权值连接成一个网络后,用上标l表示从第L-1层到第L层的权值,下标ij表示从神经元j到神经元i,细心的话可以看出有点问题,为什么不是定义为输入在左边输出在右边,而是定义为输入在右边输出在左边,这明显不符合一般的理解,但是这样表示是有一定的深意的,后面我们将讲到这样做有什么好处。
然后我们看到右下角的权值矩阵,他表示第L层相对于L-1层的权值矩阵,上图中只是两列神经元节点的两两连接就有ij个权值,例如作为输出的右边第一个神经元对应左边每个神经元都有一个权值,左边有j个神经元对应右边的第一个神经元就会有j个权值,这样右边的第一个神经元就有j个权值(得到了一行权值向量),同样作为输出的右边的有i个神经元,就会有i行这样的权值矩阵。这样第L层的神经元相对于第l-1层的神经元的权值就组成了一个权值矩阵W。这样就解释了为什么Wij将输出i卸载左边,而输入j写在右边的道理。
当然进一步的,如果是一个有n层的神经网络,就会有n组这样的W权值矩阵。
-
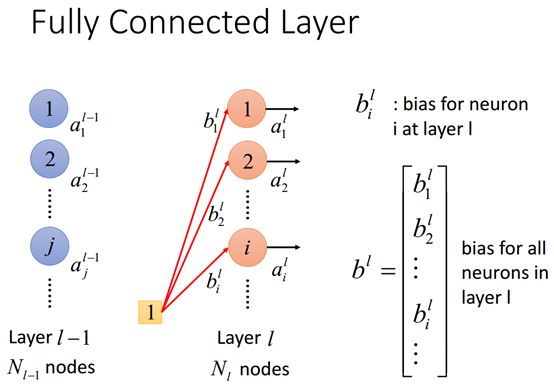
偏置矩阵向量
不要忘了还有bias,但是往往论文中常常不会将bias写出来,因为我们通常可以将bias认为是权值w的一部分而一同写在w里,上图中我们可以看到第L层上的第i个神经元上的bias,同样i个神经元的bias可以组成一个列矩阵。
-
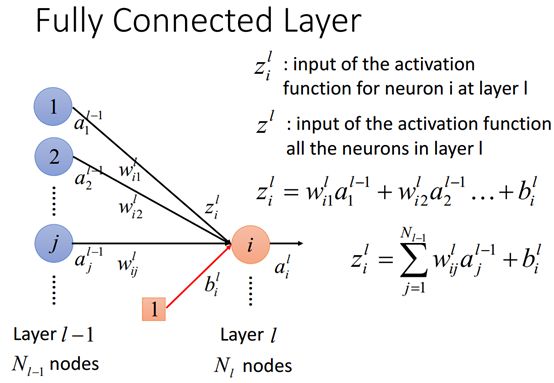
激活函数的输入Z
在介绍了全连接层权值和bias后我们还有激活函数的输入,Z加入了下标的i的就表示第L层的输入i神经元的激活函数的输入,当然我们也用Z加上一个上标l表示所有输入神经元的激活函数的输入。我们可以看到每一条神经元连接线上的权值w和a的乘积之和就为Z加上一个上标,也就事表示所有的激活函数的输入。
注意:Wij一定是从j指向i的,例如Wi1表示1指向i的连接之间的权值向量w.
-
激活函数的输入Z与L-1层神经元之间的关系
我们前面知道如何计算z也就是第L层级的激活函数输入,现在我们计算所有层i的Z, 看上图我们可以很清楚的看到如果有i层,则Z可以写成权值矩阵w和L-1层输入举证乘积再加上bias。这里值得注意的是,如果前面我们的i(输出)和j(输入)的定义相反的话,我们这里的W就必须写成W的装置。所以这也是为什么有些文献写成W的装置而有些问些就直接写成我们这里的W。这也进一步解释了我们为什么前面要将Wij不是定义为输入在左边输出在右边,而是定义为输入在右边输出在左边。
-
激活函数的输入Z与L层神经元之间的关系
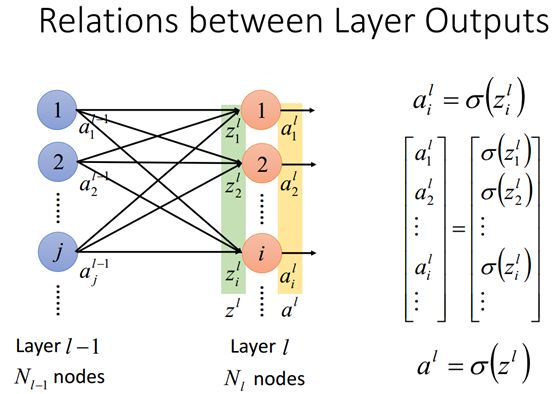
我们再看激活函数的输入z和输出a之间的关系,假设神经元的激活函数是Sigma,则将z带入到Sigma中去就得到输出某一个输出神经元a,所有的a要也可写成矩阵得表达式,也可以简便的写成右下角的式子,表示L层上每一个a。
-
L层输出与激活函数、权值向量、偏执之间的关系
在得到前面的各个层次的所有参数之间的关系之后我们就可以很自然的知道全连接网络的第L层神经元输出与激活函数等之间的关系。如上图。
-
Recurrent结构(RNN)
Recurrent的结构有一种说法就是它使得神经网络有了记忆,这是一个比较潮的说法,但是更确切一点的说就是同一个结构(网络)被反复的应用,Recurrent的优势在于输入是一个比较复杂的序列的时候,由于它是反复应用同一个结构,所以无论我们的输入的序列有多长,我们的网络所需要的参数量都一样,不会随着输入序列的长度的变化而变化。
关于RNN,我们可以参考教科书<
> -
-
RNN
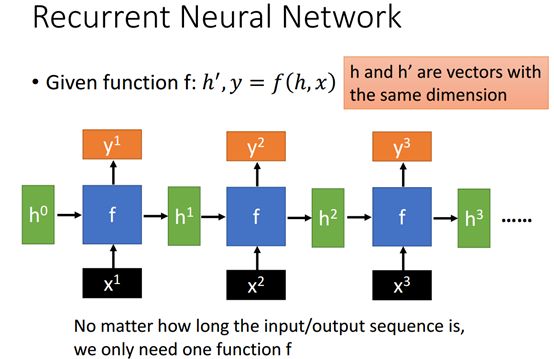
假设我们有一个给定的函数f,这个f具体是一系列的矩阵运算,也就使我们的神经网络结构组成的一个函数,通过这个函数我们会得到一些输出。
我们看到上面的示意图,一个单独的f有两个输入和两个输出,如第一个,输入为h0和x1输出则为h1和y1,RNN有一个特点就是f会被反复的使用,所以我们看到如果有一个新的输入x2给定,同样的f会以h1和x2为输入经过f后得到输出h2和y2,以此类推下去。需要强调的因为每一级的h都做为输入给f所以设计模型的时候h和h'的维数必须一致,所以h0和h1等等后面的h的维数都是一致的。
前面我们说过RNN的精髓是反复应用同一个结构,无论我们输入的序列有多长都不会影响我们的参数量,因为我们用的都是同样一个f。但是处理序列数据的时候是否只有RNN可以处理呢,当然不是,普通的前馈神经网络同样也可以,但是为什么我们选择RNN呢,因为加入序列很长,它的确可以很长,这时候如果其他的网络在输入层就会有一个很大的向量,并且参数一多就容易过拟合,即使你在训练集上拿到一个比较好的结果。但是如果你用RNN就不一样,它的参数比较少,虽然比较难在训练集上拿到一个比较好结果,但是一旦你训练好了,就比较不容易过拟合,比较容易在测试集的到好的结果。
-
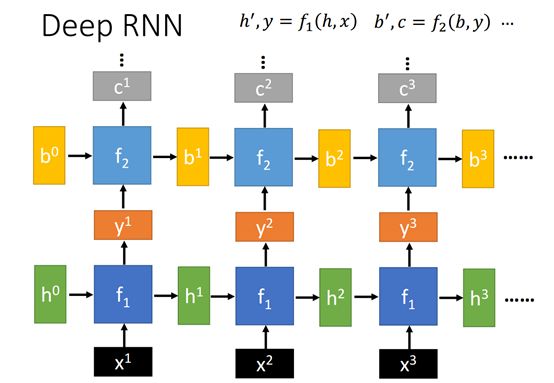
RNN当然也可以做Deep,如上图,只要保证输入到f的维数一样即可。
-
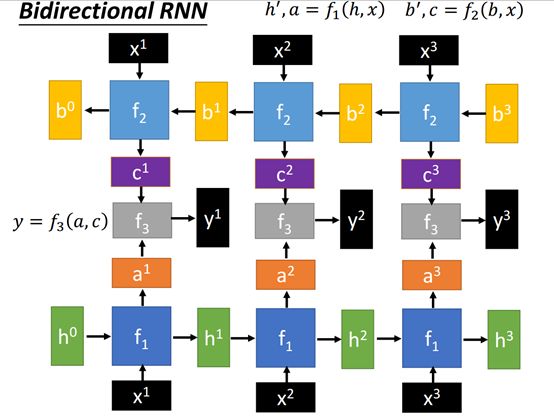
Bidirectional RNN
双向RNN其实也一样,下面的是前向的部分,上面的是反向的部分,中间通过一个f3把上下串联起来,其中每一级的c和a作为它的输入。F可以根据实际的需要进行设计。
-
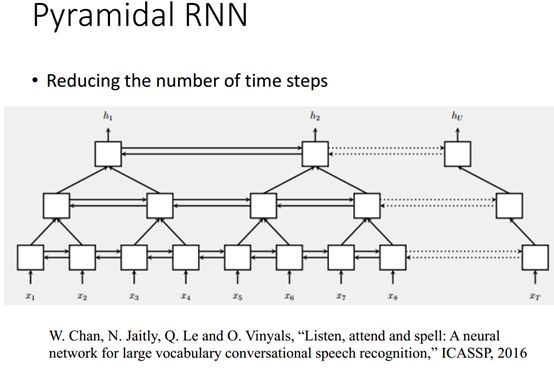
Pyramidal RNN
我们现在有一个很长的输入序列,可以看到这是一个双向的RNN,上图是谷歌的W.Chan做的一个测试,它原先要做的是语音识别,他要用序列到序列的模型做语音识别,序列到序列就是说,输入一个序列然后就输出一个序列。
最开始的时候W.Chan用的是一般的RNN,训练了几个月都没有收敛,到最后他用了Pyamidal RNN,用PyamidalRNN训练速度就会快很多,因为我们知道序列越长你需要运算量就越大,而这种金字塔型的RNN,有一个很长的序列作为输入,并且是一个bidirectional RNN也就是双向的RNN,然后用每一层的两个或是多个输出喂给下一层作为输入,这样做有一个好处是每一个层级的序列都在变短,但是反过来每一层f的输入也变多(相对单一序列),这样运算量似乎也没有减少多少。我们知道每一个层的f的运算是可以并行的,而一个序列的运算则不能够并行,因为他必须是一个输入到f输出然后喂给下一个输入,从这个角度来看,运算量还是可以接受的,特别是在原始输入序列较短的时候还是有优势的。
-
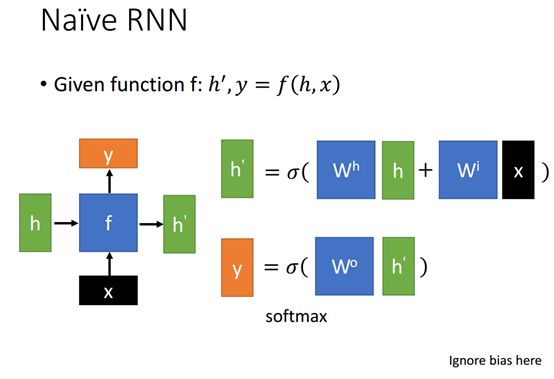
Naïve RNN
Naïve RNN也非常简单,我们可以把h和x想象成L-1到L层的输入,每个输入和他对应的权值矩阵相乘,得到的乘积相加的结果和sigmoid激活函数相乘得输出h',激活函数可以其他函数,同理可以算得到y,但是这里的y是通过h'算出来的,注意:这里是忽略了bias,但是它是必须的,只是没有写在公式里。
另外如果y是最后一层,并且希望他的输出是一个机率的话,激活函数就可以用一个softmax函数。
以上是一个最简单的Naïve RNN.
-
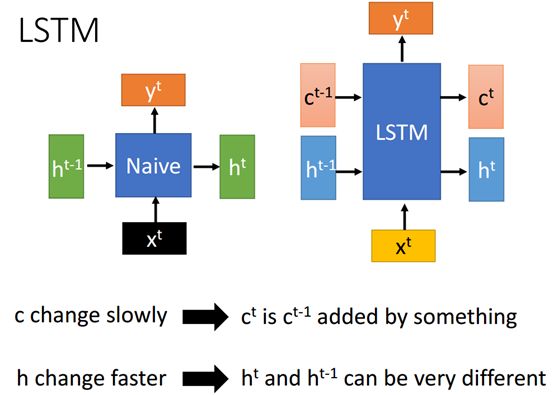
LSTM详解
上图我们看到Naïve的RNN和LSTM在结构上的区别,似乎LSTM只是在输入端多了一个输入Ct-1,输出也只是相应的多了一个Ct,为什么不可以将输入端的Ct-1和Ht-1合并在一起看成一个整体呢?
因为c和h有比较大的不同,Ct-1和Ct的关系是Ct-1加上一些东西后得到Ct,并且C改变的很慢。而H则不同,它的变化非常快,并且Ht和Ht-1有很大的不同。
上面的意思就是说LSTM在将信息传递到下一层级的时候有两条路径,一条路径比较快,另一条路径则比较快,慢的路径可以记住比较久的一些信息。
-
计算LSTM四个z
LSTM的输出是如何计算得来的呢,看到上图应该比较好理解了:
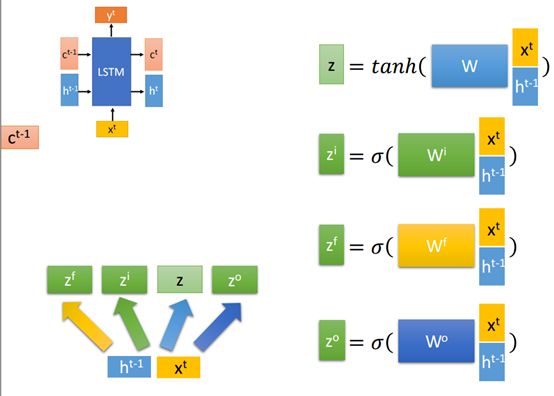
LSTM中我们前面讲到的我们有3个输入t-1上标的c、h和t上标的x,经过LSTM后得到3个t做为上标的c、t、y,将t上标x和t-1上标的h分别乘上四个不同的权值向量w然后乘上激活函数分别得到四个不同的向量t。
另外,这四个计算是可以并行运算的,当然现在的一些LSTM的库已经都给做好了,但是我们不要忽略了这个细节,往后深入看到实现代码的时候我们可以看到它是如何实现的。
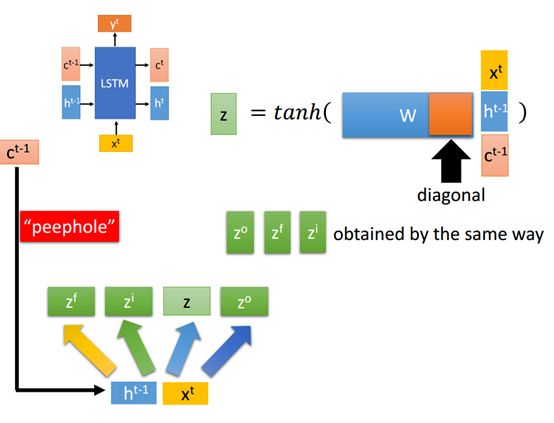
通常也可以将t-1下标的c和其他两个输入接在一起,如上图所示,这种形式叫做"peephole",也就是窥视孔,如果接在一起,我们可以看到右上角的计算z的时候w的也相应的变长,但是在实际操作中会将w其中的一部分强制的矩阵变成diagonal,也就是对角线的。
其他的几个输出z的和上面的描述一样。
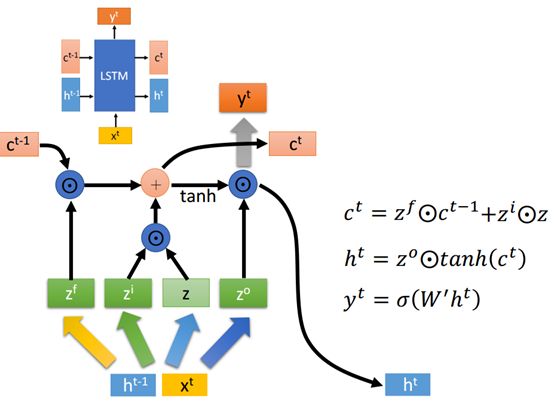
上面的步骤我们通过计算得到了四个不同的向量z,我们先将中间的两个向量上标为i的z和z相乘,当然这两个向量的维数必须是一样的。然后将c和f上标的z相乘的到结果与前面的结果相加,得到下一个时间点的Ct,注意相乘的操作(圆圈中间加点)也都是element wise operation。
其中上标为i的z就是input gate,它决定z的信息能否流入。
上标为f的z是forget gate,它决定c的memory能否被传入到下一个时间点。
ht是ct取tanh后与Z0进行element wise 操作得到的结果。
Yt则是ht乘上激活函数sigmoid。
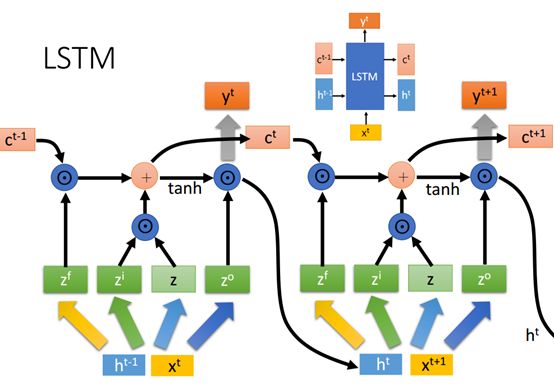
于是我们就得到ct和ht与新加入的xt+1作为为输入喂到下一个LSTM模型,反复利用。看下图:
如上面所描述的ct和ht与新加入的xt+1作为为输入喂到下一个LSTM模型,然后在得到一组新的ct和ht在喂给下一个LSTM, 如此反复,和普通的RNN是一样的。
-
GRU
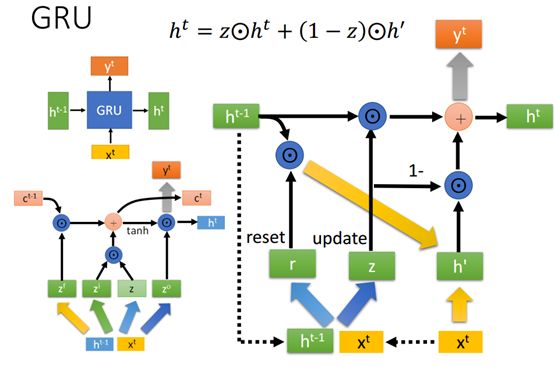
GRU是gate recurrent unit的缩写,它现在有取代LSTM的趋势,就大的架构来说GRU和Naïve RNN 很像,它没有LSTM那一样的变化很慢的和变化很快的输入,在外观上和一般的RNN是一样的,但是在它的内部就有很大的不同。
-
GRU结构
如下图:
Ht-1和xt并在一起乘上一个蓝色箭头表示的矩阵再通过激活函数的到r,r为reset gate,另一边通过乘以另外一个矩阵在激活函数激活之后得到z,z为update gate。
Ht-1和r做element wise operation的到一个新的向量后与xt并在一起乘以一个黄色箭头表示的矩阵的到h'。
Ht-1与z做element wise operation的结果在与h'做element wise相乘得到ht。
相对于LSTM而言,我们可以把上图中的下面这一路中的输出看成是forget gate
把下图中的这一路的输出看成input gate
把input gate 和forget gate的输出加起来就得到新的memory ht,然后让它在下一个时间
点再算一次output gate。
-
GRU的优势
上边的每一个颜色的箭头表示一个矩阵,我们可以看到LSTM有四个不同颜色的箭头,而GRU只有3个不同颜色的箭头,也就是说LSTM的输入要乘上四个不同的向量矩阵,而GRU的每个输入只要成上三个不同的向量矩阵,所以说GRU相对于LSTM,运算量会比较小,进一步的GRU所用的参数就会较少,也就更加不容易过拟合。
-
Stack RNN
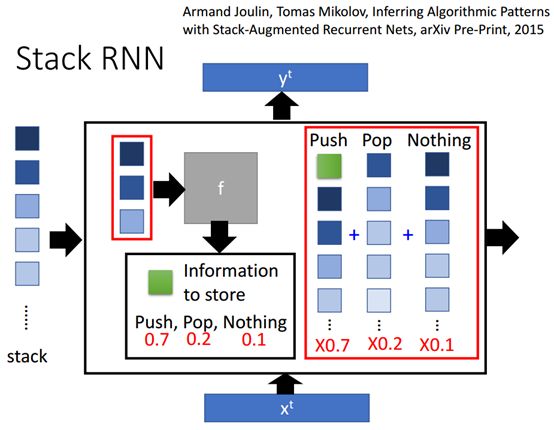
Stack RNN的特点是输入可以很大,甚至是无穷大,一般的RNN例如LSTM随着输入变大模型训练的参数也随之变多,很容易导致过拟合。但是Stack RNN就不一样,它需要的参数量和输入的大小是不相关的,所以就算输入是无穷大也无所谓。
看上图,Stack RNN的输入是一个叫做stack的序列,左边红色方框中一列输入只有3个,也就是说Stack RNN不会用所有的stack作为输入,而只是取其中的一部分,取几个stack做为输入可以由模型的设计者自己自行决定,例子里是序列的前几个。
Stack RNN会将输入的stack喂入一个f的函数,然后函数会输出要放到stack里面的信息,另外还会输出push,pop,nothing。
Push就是说将经过f后得到的信息(绿色),push到stack里面最前面。
Pop就是说将stack最上面的一个元素弹出,这里将stack中最上面的一个深蓝的stack弹出了。
Nothing就是什么都不做。
给push、pop和nothing这三个运算添加一个权值,也就是说对stack分别做push、pop和nothing这三个操作,然后分别得到三个stack,然后分别乘以三个操作的比重值分别是0.7、02和0.1最后相加得到新的stack,在将新的stack传到下一个时间点。
-
卷积神经网络CNN
CNN首先得目标同样是为了简化神经网络,所以CNN所需要的参数量比全连接的神经网络更少。
-
-
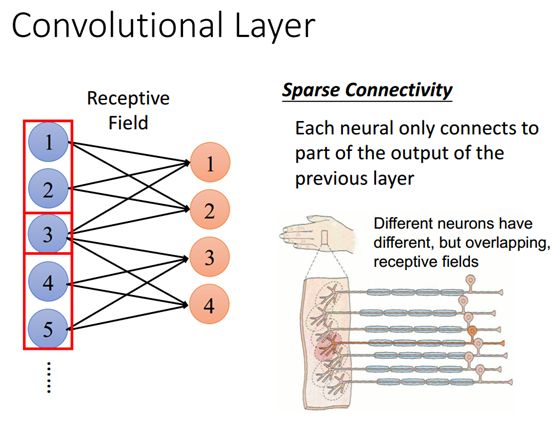
稀疏连接
上面1~5是前一层的输出,1~4是下一层的输出,如果是全连接层的话,就会要考虑前一层所有的输出以后才决定下一层一个神经元,这一层上的每一个神经元都需要考虑前一层的所有的神经元。如果是CNN,就是稀疏连接,也就是每一个神经元值会连接到前一层的部分输出,如上图所示的红色的这一层只是连接了前一层的前面3个输出,至于这个部分是多少,是3个还是多个,就有神经网络模型的设计者自己决定。
这个被连接的前一层的部分神经元叫做"感受野",就好皮肤上的一歌神经元只管皮肤的一小部分。
-
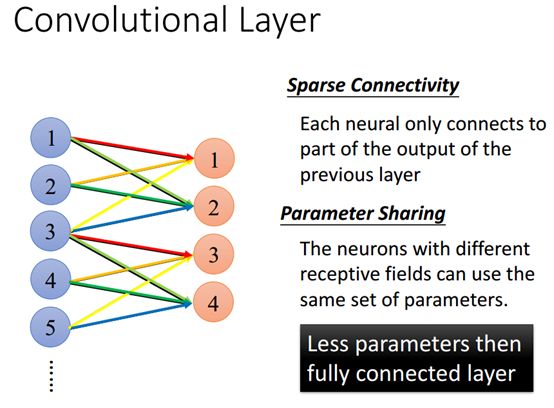
参数共享是指不同神经元可以由不同的参数,当然这里的不同是指不同的感受野的神经元有不同的参数,如果是让同一个感受野的神经元有同一样的参数,那就没有什么意义。
这里假设第一个和第三个神经元共享一个同样的参数,第二个和第四个神经元贡献一个同样的参数,这样我们就可以看出稀疏连接和参数贡献特性的神经网络比全连接的神经网络拥有更少的参数。
-
Filter
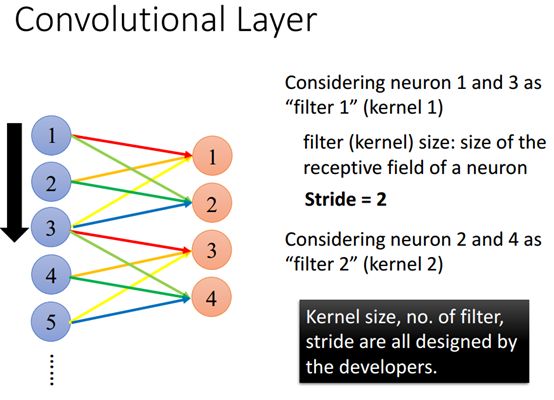
如果现在我们有不同的神经元但是他们的参数是共享的,这组参数叫做"filter",也叫做kernel。
Filter(kernel) size的意思是说一个神经元的感受野的大小,这里1~3是kernel1的感受野,所以filter1(kernel1) 大小就是3,同理filter2(kernel2) 大小也是3。
Stride的意思是感受野和感受野之间的间距。
-
一维单通道CNN例子
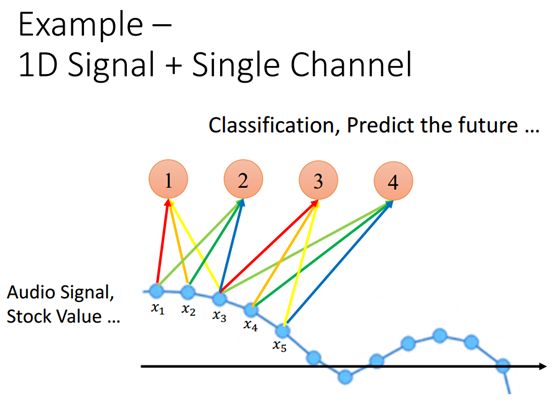
上图这个例子1维单通道的例子,是一个声音信号,x1~ x5就是声音信号的取样点。股票的上下波动也可以看成是1维单通道的例子。
如果将CNN用在这个例子上,感受野就可以是如例子上的x1~x3以及x3~x4等时间的区间,不同的感受野对应不同的filter,filter可以再接其他的CNN或是全连接的神经网络,就可以做预测、分类等不同的事情。
-
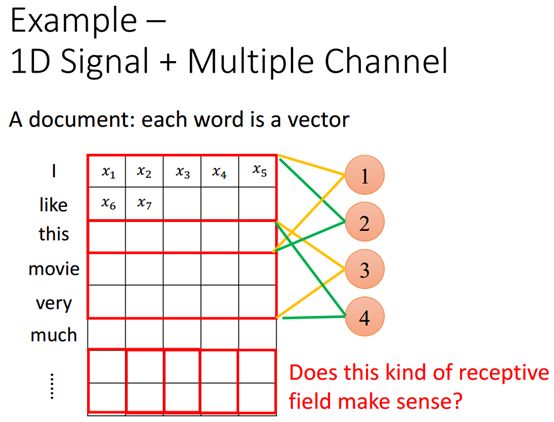
一维多通道CNN例子
如上图,multiple chanel的意思就是说在这个维度上的每一个时间点,并不是用一个value去描述它,而前面声音的例子中一个时间点我们则是用一个value取描述它。在这里我们用一个向量去描述它(word),这个向量的每一维代表了不同的通道。
-
二维单通道CNN例子
这个例子我们看到是一个6*6的黑白图片图像,感受野是3*3大小,stride是1,也就是说以1的跨度滑动。
-
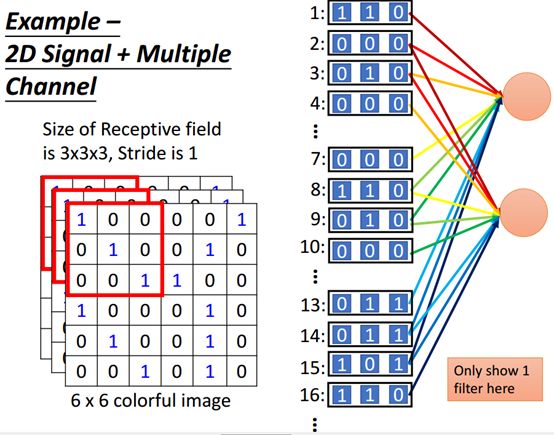
二维多通道CNN例子
上图也就是如果彩色图片,我们就可以做二维多通道的模型,其中每一个通道就表示一个颜色,而每一个像素是RGB三种颜色组成的,RGB分别就是一个通道。
二维多通道的感受野是一3*3*3的立方体,所以每个神经元是连接到27个像素。
同样如果要处理的是一个视频图像,那感受野就是思维的,每个神经元连接到一个思维的感受野有更多的像素。
-
Padding
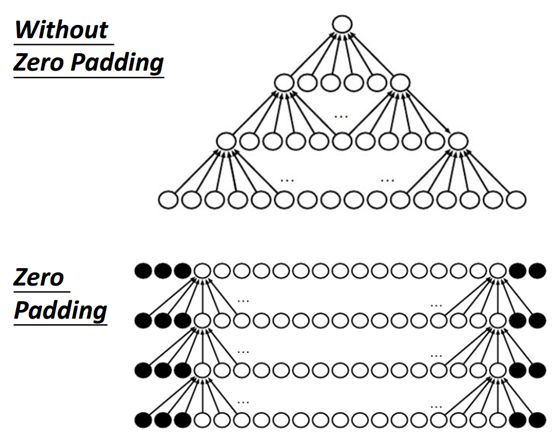
如果没有做padding(填充),那就会少考虑边缘的地方,所以你的图像就会越做越小,例如图中上部分。
也可以做zero padding,但是zero padding有很多中,你可以尝试一下看哪种效果比较好。假如我们现在有一个filter可以考虑前面的5个输入,图中的下半部分没有涂黑圈的地方就是输入,黑圈就是padding(填充)。
如果只填充两个,让每一次做卷积以后输入和输出的图像一样大。
如果感受野可以考虑5个输入,要填充4个是没有问题的,最边缘的filter还是会产生输出,如果要填充5个则不行,最边缘的输入都是0,所以最多能填充4个。
-
Pooling Layer
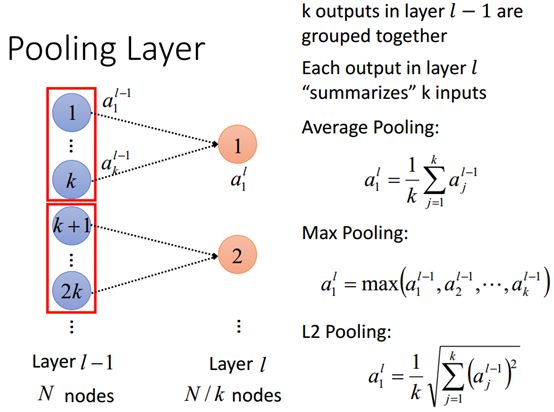
Pooling layer要做的事情是把L层的前一层L-1层的k个输出组成一群,然后L层每一个输出代表前一层k个输出的特性(也可以理解为对前面k个输出的一个概括-summarize),这就叫做pooing,如下图:
-
Pooling的层次结构
如上图,假设L层的前一层L-1层的N个节点分成k做,则L层就有N/k个节点,也就是说L层的每一个节点代表L-1层k组节点。
那么如何从L-1层中的K组节点中的每一组中选择一个节点来电表这一组节点呢?这就很多种方法,例如右边的公式给出集中方法。
首先是取每组中的一个平均值,代表这一组。
然后是取每组中的一个最大值,代表这一组。
再次是L2 pooling,也就是所有值都平方相加然后开根号再除以k。
或者上面的都不满足需求的话,还可以是上面几个方法的一个组合,着个比较灵活,可以做各式各样的尝试。
-
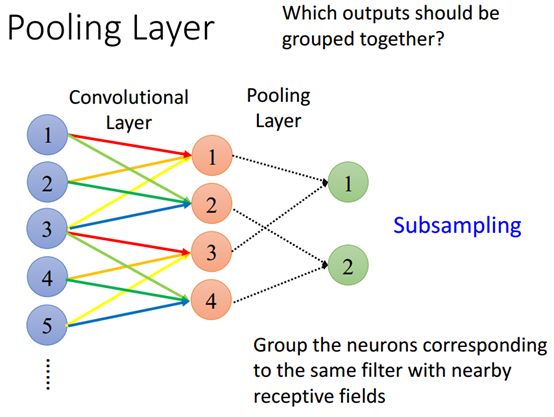
那些输出可以组合在一起?
首先如果神经元属于同一个filter,就可以将这些神经元组合在一起,也就是说同一个filter的输出组合在一起,例如上图的1和3,2和4属于同一个filter,我们就将他们组合在一起,这也是比较常见的做法,例如subsampling 即二次抽样。
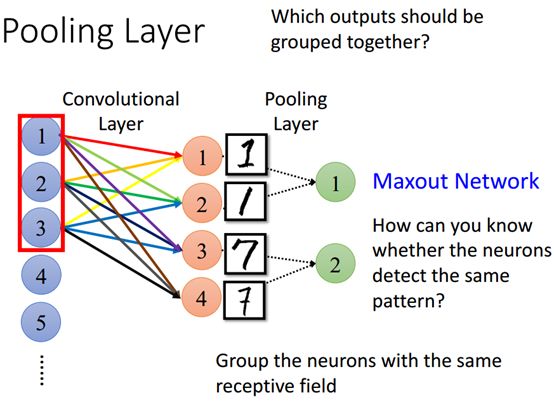
还有一些不同的方法,如上图,把不同的filter但是对应到同一个感受野的神经元组合在一起作为输出。例如上图我们的123三个神经元应用到1234四个filter,然后把12两个组合在一起,34组合在一起作为pooling输出,这也是可以的,这其实就是我们通常所说的Maxout network。
这样分组的好处是,模型可以将长得不像的东西,但是是属于同一类的东西归类在一起,例如一辆火车从不同角度看他是不一样的,在正面看它,它是一个长方形,从侧面看它它就是一个长方形。再如我们本例子中1的两种不同写法,但是我们有不同的filter来检测它,第一种filter来检测上一种1的写法(模式),另外一种filter2来检测它的另一种写法。所以不管输入的东西是什么形式,只要他属于同一类,我们就可以将它归类起来。
-
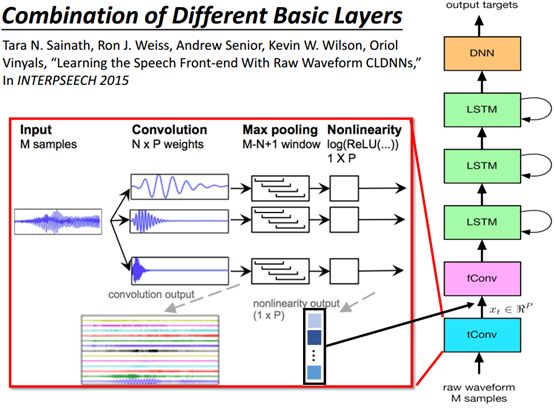
如何绑定不同神经网络结构
-