word2vec 介绍

1.背景

在NLP中，传统算法通常使用one-hot形式表示一个词，存在以下问题：

1）维度爆炸，词表通常会非常大，导致词向量维度也会非常大。

2）损失语义信息，one hot随机给每个词语进行编号映射，无法表示词语之间的关系。

所以word embeding的优势如下：

1）将词语映射成一个固定维度的向量，节省空间。

2）词向量可能会具备一定的语义信息，将相似的词语放到相近的向量空间（比如香蕉和苹果都是属于水果，苹果又会涉及到歧义问题），可以学习到词语之间的关系（比如经典的 男人-女人=国王-王后）。

本文会介绍一下Word2vec原理，这是一种常见的可以用于训练词向量的模型工具。常见的做法是，我们先用word2vec在公开数据集上预训练词向量，加载到自己的模型中，对词向量进行调整，调整成适合自己数据集的词向量。

2.训练模式

我们通常是通过将词向量用于某些任务中，用这些任务的衡量指标去衡量模型结果。

那么反过来，如果我们想要训练词向量，可以先去训练一个语言模型，然后将模型中对应的参数，作为词向量。从任务形式上看，我们是在训练语言模型，而实际上我们最终的目标是想得到词向量，我们更关心的是这个词向量合不合理。

Word2vec根据上下文之间的出现关系去训练词向量，有两种训练模式，Skip Gram和CBOW（constinuous bags of words），其中Skip Gram根据目标单词预测上下文，CBOW根据上下文预测目标单词，最后使用模型的部分参数作为词向量。

AutoEncoder也可以用于训练词向量，先将one hot映射成一个hidden state，再映射回原来的维度，令输入等于输出，取中间的hidden vector作为词向量，在不损耗原表达能力的前提下压缩向量维度，得到一个压缩的向量表达形式

2.1 CBOW

根据上下文预测目标单词，我们需要极大化这个目标单词的出现概率。

假设词表大小为V，词向量维度为N，上下文单词为x1，x2, …, xc，定义上下文窗口大小为c，对应的目标单词为y，我们将x跟y都表示成one hot形式。这里涉及到两个矩阵参数，W是词向量矩阵，每一行都是某个词的词向量v，W’可以看做是一个辅助矩阵，每一列可以看做是某个词对应的相关向量v’。

前向过程：

x->hidden：对于每个xi，取出对应的词向量vi，再对这些词向量取平均作为hidden vector，相当于通过简单粗暴的叠加，得到这些词语的语义向量。

h->y：将h乘以W’得到一个维度为V的向量u，进行softmax归一化得到概率向量，取概率最大的作为预测单词。

后向过程：

我们需要极大化目标单词的出现概率p(y | x1, x2, … , xc)，也就是极小化负对数似然函数，Loss函数定义为：

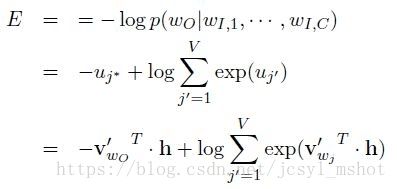
我们需要更新两个矩阵参数，W和W’，先根据loss对参数求梯度，再使用梯度下降法更新参数。具体的求导过程这里略过，请移步原论文。

对于W’，经过求导，v’更新公式为：

对于W，经过求导，v更新公式为：

2.2 skip-gram

3.训练优化

原始的方法所存在的问题是计算量太大，体现在以下两方面：

1）前向过程，h->y这部分在对向量进行softmax的时候，需要计算V次（每次除目标词的概率， 还需要计算词表中其它词的概率 ，最终才能进行softmax 归一）。

2）后向过程，softmax涉及到了V列向量，所以也需要更新V个向量。

问题就出在V太大，而softmax需要进行V次操作，用整个W进行计算。

因此word2vec使用了两种优化方法，Hierarchical SoftMax和Negative Sampling，对softmax进行优化，不去计算整个W，大大提高了训练速度。

3.1 Hierarchical SoftMax

首先我们要定义词向量的维度大小M，以及CBOW的上下文大小2c,这样我们对于训练样本中的每一个词，其前面的c个词和后面的c个词作为了CBOW模型的输入,该词本身作为样本的输出，期望softmax概率最大。

在做CBOW模型前，我们需要先将词汇表建立成一颗霍夫曼树。可以根据单词在语料中出现的次数建立。

对于从输入层到隐藏层（投影层），这一步比较简单，就是对w周围的2c个词向量求和取平均即可。

我们把之前所有都要计算的从输出softmax层的概率计算变成了一颗二叉霍夫曼树，那么我们的softmax概率计算只需要沿着树形结构进行就可以了。如下图所示，我们可以沿着霍夫曼树从根节点一直走到我们的叶子节点的词w2。

其中，根节点的词向量对应我们的投影后的词向量，而所有叶子节点就类似于之前神经网络softmax输出层的神经元，叶子节点的个数就是词汇表的大小。在霍夫曼树中，隐藏层到输出层的softmax映射不是一下子完成的，而是沿着霍夫曼树一步步完成的。

如何“沿着霍夫曼树一步步完成”呢？在word2vec中，我们采用了二元逻辑回归的方法，即规定沿着左子树走，那么就是负类(霍夫曼树编码1)，沿着右子树走，那么就是正类(霍夫曼树编码0)。判别正类和负类的方法是使用sigmoid函数，即：

我们使用最大似然法来寻找所有节点的词向量和所有内部节点θ，先拿上面的w2例子来看，我们期望最大化下面的似然函数：

在根节点处左右概率之和是1，然后在接下来的每个节点，对应两个子节点的概率值之和等于父节点本身的概率值，那么走到最后，所有叶子节点的概率值之和必定还是等于1。

Loss函数定义为：

其中n(w, i)表示从根节点到叶节点w路径中的第i个节点，v’(w, i)表示n(w, i)所对应的v’向量，L(w) 路径的长度。

通过求导也就是说，这里只需要更新L(w)-1个v’向量，时间复杂度直接从O(V)降到了O(logV)，

3.2 Negative Sampling