【机器学习】降维方法学习笔记

降维的目的：便于计算和可视化；有利于提取有效信息、摈弃无用信息

降维的主要方法：线性映射和非线性映射

 

线性映射方法里比较常见的就是：

• 主成分分析 PCA（Principal Component Analysis）
• 线性判别分析 LDA（Linear Discriminant Analysis，Fisher Linear Discriminant)

本博文主要介绍这两种线性降维方法。 

 

主成分分析 PCA

使用最广泛的非监督数据压缩算法

本质：找到一些投影方向，使得数据在这些投影方向上的方差最大，且这些投影方向相互正交。

在信号处理领域，信号具有较大方差，噪声具有较小方差，信号与噪声之比称为信噪比。信噪比越大意味着数据的质量越好，反之，信噪比越小意味着数据的质量越差。由此不难引出PCA的目标，即最大化投影方差，也就是让数据在主轴上投影的方差最大。

总之，方差越大，在该投影方向上的信息量越大。

均值：
标准差：
方差：

协方差的性质：

(X的方差)

很重要的一句话：协方差矩阵及时计算不同维度(也就是不同属性)之间的方差

PCA是一种线性降维方法，虽然经典，但具有一定的局限性。可以通过核映射对PCA进行扩展得到核主成分分析（KPCA），也可以通过流形映射的降维方法，比如等距映射、局部线性嵌入、拉普拉斯特征映射等，对一些PCA效果不好的复杂数据集进行非线性降维操作。

总结一下算法的步骤：(假设有n条具有m个属性的数据)

1. 组成m行n列的矩阵X
2. 对x的每一行(每一个属性字段)进行均值化mean
3. 将矩阵进行中心化(每一维减去该维度的均值)
4. 求出上面的矩阵的协方差矩阵C
5. 求出C的特征值和特征向量
6. 将特征向量按特征值排序，去前K行组成矩阵P(也就是最终的投影面)
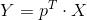7. 就是降维为K维之后的数据
8. 恢复原数据

 

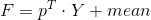
# coding=utf-8
from numpy import *

'''
通过方差的百分比来计算将数据降到多少维是比较合适的，
函数传入的参数是特征值和百分比percentage，返回需要降到的维度数num
'''
def eigValPct(eigVals,percentage):
    sortArray = sort(eigVals)  # 使用numpy中的sort()对特征值按照从小到大排序
    sortArray = sortArray[-1::-1]  # 特征值从大到小排序
    arraySum = sum(sortArray)  # 数据全部的方差arraySum
    tempSum = 0
    num = 0
    for i in sortArray:
        tempSum += i
        num += 1
        if tempSum >= arraySum*percentage:
            return num

'''
pca函数有两个参数，其中dataMat是已经转换成矩阵matrix形式的数据集，列表示特征；
其中的percentage表示取前多少个特征需要达到的方差占比，默认为0.9
'''
def pca(dataMat,percentage=0.9):
    meanVals = mean(dataMat,axis=0)  # 对每一列求平均值，因为协方差的计算中需要减去均值
    meanRemoved = dataMat-meanVals
    covMat = cov(meanRemoved, rowvar=0)  # cov()计算方差
    eigVals,eigVects = linalg.eig(mat(covMat))  # 利用numpy中寻找特征值和特征向量的模块linalg中的eig()方法
    k = eigValPct(eigVals,percentage)  # 要达到方差的百分比percentage，需要前k个向量
    eigValInd = argsort(eigVals)  # 对特征值eigVals从小到大排序
    eigValInd = eigValInd[:-(k+1):-1]  # 从排好序的特征值，从后往前取k个，这样就实现了特征值的从大到小排列
    redEigVects = eigVects[:, eigValInd]   # 返回排序后特征值对应的特征向量redEigVects（主成分）
    lowDDataMat = meanRemoved*redEigVects  # 将原始数据投影到主成分上得到新的低维数据lowDDataMat
    reconMat = (lowDDataMat*redEigVects.T)+meanVals   # 得到重构数据reconMat
    return lowDDataMat, reconMat

if __name__ == '__main__':
    t = [[1, 2, 3], [3, 3, 6], [4, 6, 8], [4, 7, 7]]
    lowDDataMat, reconMat = pca(t)
    print('lowDDataMat', lowDDataMat)
    print('reconMat', reconMat)

 

线性判别分析 LDA

有监督的线性降维算法

本质：找到一些投影方向，使得数据在这些投影方向后类内方差最小、类间方差最大。(高内聚，低耦合)

 

总结一下算法的步骤：(假设有两类数据)

1. 第i类数据的集合，其均值为，协方差矩阵i
2. 两类样本的中心在直线上的投影为：和
3. 两类样本的协方差0和1
4. 同类样例的投影尽可能接近，0+1尽可能小
5. 异类样例的投影点尽可能远离，尽可能大
6. 从而

 其中，

类间散度矩阵 ；类内散度矩阵 =0+1

LDA的目标：最大化广义瑞利商(其中，w成倍缩放不影响J值，仅考虑方向)

 

# LDA
''''''
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_classification,make_multilabel_classification


def LDA(X1, X2, y):
    # print(X1)
    # print(X2)
    len1 = len(X1)
    len2 = len(X2)
    print(len1, len2)
    u1 = np.mean(X1, axis=0)  # 求均值
    u2 = np.mean(X2, axis=0)
    print(u1, u2)
    cov1 = np.dot((X1 - u1).T, (X1 - u1))   # 计算协方差
    cov2 = np.dot((X2 - u2).T, (X2 - u2))
    Sw = cov1 + cov2    # 类内散度矩阵
    w = np.dot(np.mat(Sw).I, (u1 - u2).reshape((len(u1), 1)))
    print('w', w)
    X1_new = np.dot(X1, w)
    X2_new = np.dot(X2, w)
    y1_new = [1 for i in range(len1)]
    y2_new = [2 for i in range(len2)]
    return X1_new, X2_new, y1_new, y2_new


if '__main__' == __name__:
    # 用scikit-learn的接口来生成数据,设置随机数种子，保证每次产生相同的数据。
    X, y = make_classification(n_samples=200, n_features=2, n_redundant=0, n_classes=2, random_state=2)
    X1 = np.array([X[i] for i in range(len(X)) if y[i] == 0])
    X2 = np.array([X[i] for i in range(len(X)) if y[i] == 1])
    
    X1_new, X2_new, y1_new, y2_new = LDA(X1, X2, y)
    plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
    plt.show()
    plt.plot(X1_new, y1_new, 'b*')
    plt.plot(X2_new, y2_new, 'ro')
    plt.show()

 

参考文献

1. [机器学习笔记]主成分分析PCA简介及其python实现(本博文中代码来源)

2. PCA （主成分分析）详解 （写给初学者）(这篇看完可以很好地理解PCA)

3. 线性判别分析（LDA）基本原理及实现

4. 线性判别分析(LDA)和python实现（二分类问题）(本博文中代码来源)

5. 数据降维方法小结

6. 机器学习降维方法概况

 之前的博文里提到一道相关的的题目可供参考：杂谈：几个知识点整理