强化学习算法学习汇总笔记 (一) — Q-learning、Sarsa、DQN、Policy Gradients
一. 强化学习的分类
1.Model-free 和 Model-based
Model-free 即机器人不知道外界环境信息,只能在机器人执行每一步动作后从环境中得到反馈然后去学习,只能按部就班,一步一步等待真实世界的反馈,再根据反馈采取下一步行动。诸如Q Learning, Sarsa,Policy Gradients等算法。
Model-based 指机器人对环境有一定的了解,可以对环境进行建模,通过模型机器人再也不必等真实世界的反馈做出动作。可以这么理解,当机器人要学习的时候,由于有了环境的模型,机器人可以将建立的环境模型当做是真实世界,不断的学习。在模型世界中,选择学习情况最好的那一种。
2.基于概率和基于价值(value)
基于概率:是强化学习中最直接的一种,通过state(观测)直接输出下一步采取的action(动作)的概率,然后根据概率采取行动,所以每一种action(动作)都有可能被选中,只是可能性不同。诸如 Policy Gradient。
基于价值:输出所有动作的价值,相比基于概率的方法,基于价值的决策部分更为铁定,即选择价值最高的。诸如 Q Learning, Sarsa 等算法。
同时也有结合这俩种方式的算法,诸如Actor-Critic,在Actor-Critic 基础上扩展的 DDPN (Deep Deterministic Policy Gradient)、A3C (Asynchronous Advantage Actor-Critic)、DPPO (Distributed Proximal Policy Optimization)。
3.回合更新(Monte-Carlo update,蒙特卡洛更新)和单步更新(Temporal-Difference update)
回合更新:指游戏开始到结束整一个过程,只有等到结束后,才能够总结这个回合的所有转折点,再更新我们的行为准则。诸如Monte-carlo Learning 和 基础版的 policy gradient等。
单步更新:在游戏中的每一步都可以更新其行为准则(例如如何选择action等),不用等到整个过程都结束。诸如Qlearning、Sarsa 和升级版的 policy gradient 等都是单步更新的。
4.在线学习(On-Policy)和 离线学习(Off-Policy)
在线学习(On-Policy):在当前时间当前采取的动作紧接着通过得到的反馈下进行学习。诸如 Sarsa 算法 和 Sarsa lambda 算法。
离线学习(Off-Policy):可以根据过往的经验及数据进行学习,举个例子,就是白天收集的数据可以在晚上通过离线学习进行。诸如 Q-Learning,Deep-Q-Network 等算法。
二. Q-learning
1.基本概念
a.假设我们现在处于状态s1(在写作业),有俩个行为,分别是a1(看电视),a2(写作业)。根据经验,在这种状态下,选择a2(写作业)的值(value,可理解为分数)要比选择a1(看电视)要高。这里的state(状态)、action(动作)、值(value)都可以用一个有关s、a和value的Q表格代替。
b.在这个例子中,在状态s1下选择a1的值为 Q(s1,a1)=-2, 选择a2的值为 Q(s2,a2)=2, 所以我们选择a2这个动作然后到达状态s2。重复上面的过程,我们可以得到Q(s2,a1), Q(s2,a2) 的值(value),并比较他们的大小,从而确定下一个action(动作)达到状态 s3,并不断的重复这个过程,这就是Q表,如下图所示。 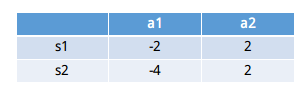
2.Q-learning 的更新
如何去更新Q表中的值?
根据Q表的估计,因为在状态s1中,a2的值比较大,通过之前的决策方法,我们在s1采取了a2,并达到了s2状态,这时候我们开始更新用于决策的Q表。在s2状态下,我们通过某种手段得到了在s2状态下采取某种action的值,分别是Q(s2,a1) 和 Q(s2,a2), 这时候对于 Q(s1,a2),我们可用如下公式更新Q(s1,a2)的值:
Q(s1,a2)=Q(s1,a2)+α[R+γ∗max Qa(s2,a)−Q(s,a)]
其中R为达到s2状态是所获得的奖励,γ
为衰减因子, α为学习效率。在这里值得注意的是,我们用maxQ(s2,a) 估算了s2的状态,但是还没有做出任何的action(动作),需要等到更新完后再做出action。
这就是off-policy 的 Q learning 是如何决策和学习优化决策过程的。
3.伪代码
Initialize Q(s,a) arbitrarily
Repeat(for each episode):
Initialize s
Repeat (for each step of episode):
Choose a from s using policy derived from Q (e.g., greedy) (上面的更新过程我们就是用了贪婪算法)
Take action a,observe r,s'
Q(s,a)<-Q(s,a)+ \alpha[r+ \gamma* \underset{a'}{max} Q(s',a') - Q(s,a)] (该公式为latex语言)
s<-s';
until s is terminal- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
伪代码概括了Q-learning中的所有内容,每次更新都用到了Q(s’,a’) 和 Q(s,a)。在choose a from s using policy derived from Q中,我们还有时会用到 ϵ−greedy
是对未来 reward 的衰减值。
4.Q-Learning 中的 γ
对于单纯考虑状态s的Q而言(不考虑在某一个状态下采取了什么动作),我们可以重写Q(s1)公式:
Q(s1)=r2+γQ(s2)=r2+γ[r3+γQ(s3)]=r2+γ[r3+γ[r4+γQ(Q4)]]=...
考虑下不同情况的 γ
值:1. γ=1情况下, Q(s1)=r2+1∗r3+1∗r4+1∗r5...
2. 0<γ<1 情况下, Q(s1)=r2+γ∗r3+γ2∗r4+γ3∗r5+...
3. γ=0情况下, Q(s1)=r2
具体代码实现请见:莫烦PYTHON Q-learning算法更新和思维决策
三. Sarsa
1.基本概念
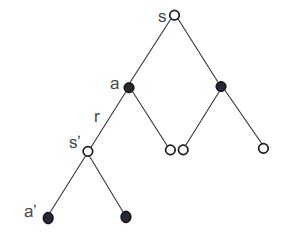
由于在前面已经介绍了Q-learning,所以将Sarsa与Q-learning做对比,如下图所示,Q-learning 在从状态s−>s′
2.伪代码
Initialize Q(s,a) arbitrarily
Repeat(for each episode):
Initialize s
Repeat (for each step of episode):
Choose a from s using policy derived from Q (e.g., greedy) (这里也可以是 \epsilon-greedy)
Take action a,observe r,s'
Choose a' from s' using policy derived from Q(e.g., greedy)
Q(s,a)<-Q(s,a)+ \alpha[r+\gamma*Q(s',a')-Q(s,a)]
s<-s';a<-a';
until s is terminal- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
3.Sarsa- lambda
从上面可知lambda是一种 on-policy算法,而lambda则代表Sarsa算法走几步更新一次自己的行为准则。例如 Sarsa(0) 指的是走完这一步以后直接更新行为准则。Sarsa(1) 指的是走完这一步,再走一步,然后再更新。Sarsa (n) 指的就是走完这一步,再走n步了,实际上已经跟回合更新差不多了。
具体代码实现请见:莫烦PATHON Sarsa算法更新和思维决策
四. DQN (Deep Q Network)
DQN 论文:Playing Atari with Deep Reinforcement Learning
1.基本概念
对比于Q-Learning 和 Sarsa 等算法,DQN 融合了深度学习的算法。具体的说,在Q-Learning中,我们提到了用Q表来存储当前状态s1下采取的动作action的值(value,在Q表中也称为Q值)。但是在实际过程中,一个状态s1到下一状态s2,这里的s2可能有很多不同的情况,这将会导致Q表存储的值会很多,不仅占内存,且在搜索的时候也是十分耗时的。 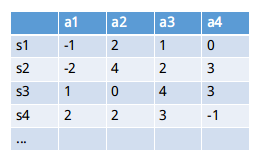
由于神经网络是个回归过程,当经过大量数据训练后,我们可以通过神经网络来预测我们Q值。即输入为状态s和动作a,得到所有的动作值(Q值)。还有另外一种形式是,只输入状态值,然后输出所有的动作值,然后按照Q-Learning的原则,直接选择拥有最大值的动作当做要采取的动作。
2. 更新神经网络
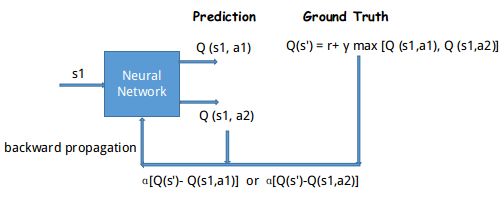
对于输入状态s1,在神经网络中通过正向传播 (forward propagation) ,输出动作的值Q(s1,a)(预测值, 可能有多个)。了解深度学习的都清楚,神经网络是需要训练的,即需要更新其网络参数,所以需要真实值与预测值来构建代价函数,实现反向传播(backward propagation)。
在强化学习训练神经网络过程中,我们需要a1,a2,…正确的Q值,这个Q值可以用Q-Learning 中的Q现实来代替, 即
Q(s′)=R+γ∗max Qa(s1,a)
。
如上图所示,我们通过NN预测Q(s1,a1)
和 Q(s1,a2), 为估计值。然后我们用上面提到的 Q(s′) 作为真值,用来更新网络参数。所以神经网络的参数就是老的NN参数 加上 学习率 α 乘以Q现实( Q(s′))和Q( Q(s1,a1)和Q(s1,a2))估计的差距。
3.Experiment replay and Fixed Q-targets
a. Experiment replay: DQN 有一个记忆库用于学习之前的经历。Q-Learning 是一种 off-policy 离线方法,可以学习当前经历的,也能学习过去的,甚至学习别人经历的。每次DQN更新的时候,都会从之前的经历进行学习。随机抽取的做法打乱了经历的之间的相关性,使得神经网络的更新更有效率。
b. Fixed Q-targets: 在DQN中,会用到俩个网络结构相同但是参数不同的神经网络,预测Q估计的神经网络具备最新的参数,而预测Q现实的神经网络则使用的参数则是很久之前的。
4.DQN的俩个神经网络
为了使用Tensorflow来实现DQN,需要构建俩个神经网络,其中target_net 用于预测q_target值,不会及时更新。而eval_net 用于预测q_eval, 这个神经网络拥有最新的神经网络参数,但是这个神经网络结构是完全一样的,这就是Fixed Q-targets。 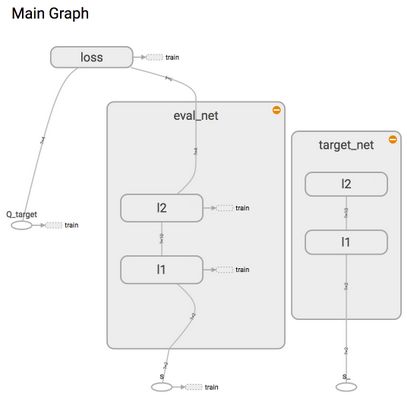
通过创建俩个神经网络,其架构一样,其中target_net 是eval_net 的一个历史版本,拥有eval_net 很久之前的一组参数,而且这组参数被固定一段时间,然后再被eval_net 新参数所替换。而eval_net 中的参数是不断的更新的,是一个可被训练的网络。
具体代码见:莫烦PYTHON DQN 神经网络 及 思维决策
手动编环境是一件耗时间的事情,而OpenAI gym 为我们提供了很多优秀的模拟环境,各种RL算法都能使用这些环境,安装gym的命令如下:
$ apt-get install -y python-numpy python-dev cmake zlib1g-dev libjpeg-dev xvfb libav-tools xorg-dev python-opengl libboost-all-dev libsdl2-dev swig
# python 2.7, 复制下面
$ pip install gym[all]
# python 3.5, 复制下面
$ pip3 install gym[all]- 1
- 2
- 3
- 4
- 5
- 6
- 7
除了传统的DQN外,还有Double DQN, Dueling DQN 等。
网络结构的代码如下所示:
def _build_net(self):
# ------------------ all inputs ------------------------
self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s') # input State
self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_') # input Next State
self.r = tf.placeholder(tf.float32, [None, ], name='r') # input Reward
self.a = tf.placeholder(tf.int32, [None, ], name='a') # input Action
w_initializer, b_initializer = tf.random_normal_initializer(0., 0.3), tf.constant_initializer(0.1)
# ------------------ build evaluate_net ------------------
with tf.variable_scope('eval_net'):
e1 = tf.layers.dense(self.s, 20, tf.nn.relu, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='e1')
self.q_eval = tf.layers.dense(e1, self.n_actions, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='q')
# ------------------ build target_net ------------------
with tf.variable_scope('target_net'):
t1 = tf.layers.dense(self.s_, 20, tf.nn.relu, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='t1')
self.q_next = tf.layers.dense(t1, self.n_actions, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='t2')
with tf.variable_scope('q_target'):
q_target = self.r + self.gamma * tf.reduce_max(self.q_next, axis=1, name='Qmax_s_') # shape=(None, )
self.q_target = tf.stop_gradient(q_target)
with tf.variable_scope('q_eval'):
a_indices = tf.stack([tf.range(tf.shape(self.a)[0], dtype=tf.int32), self.a], axis=1)
self.q_eval_wrt_a = tf.gather_nd(params=self.q_eval, indices=a_indices) # shape=(None, )
with tf.variable_scope('loss'):
self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval_wrt_a, name='TD_error'))
with tf.variable_scope('train'):
self._train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
五. Policy Gradients
强化学习是一个通过奖惩来学习正确行为的机制,有学习奖惩值,根据自己认为的高价值选择行为的,如Q Learning、Deep Q Network 等。也有不通过分析奖励值,直接输出行为的方法,如Policy Gradient。Policy Gradient 直接输出动作的最大好处就是,能够在一个连续区间内挑选动作,而基于值的,往往是在所有动作中计算值,然后选择值最高的那个行为。
由于我们可以用神经网络来输出预测的动作,在Policy Gradient 中,可以通过reward 来进行反向传播。当Policy Gradient 输出挑选的动作的时候,根据reward的大小来调整判断该网络是否。即当Policy Gradient网络输出动作为reward 最高的时候,会使Policy Gradient输出该动作概率增大。而当Policy Gradient 网络输出的动作的reward不是那么高的时候,则相应使Policy Gradient输出该动作的概率减小。 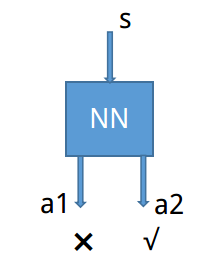
Policy Gradient 可以通过神经网络来输出一系列动作,并从中挑选,紧接着根据奖赏(reward)来调整网络的参数构。如上图所示,该网络会偏向于输出动作a2。
具体代码见 莫烦PYTHON 算法更新和思维决策