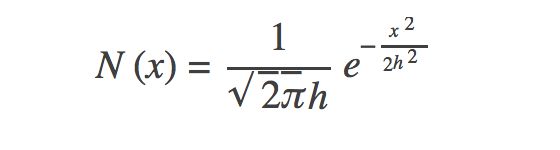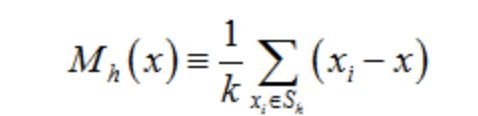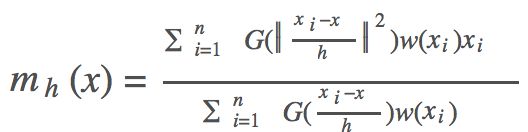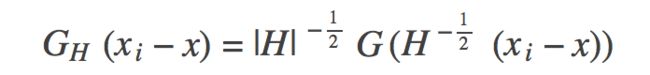MeanShift 均值漂移算法
前面说了K-Means聚类算法,这里我们介绍一种新的聚类算法:MeanShift, 它常被用在图像识别中的目标跟踪,数据聚类、分类等场景,前者的核函数使用了Epannechnikov核函数,后者使用了Gaussian(高斯核函数)
一 算法的原理理解:
1 核函数
在Mean Shift算法中引入核函数的目的是使得随着样本与被偏移点的距离的不同,其偏移量对均值偏移向量的贡献也不同,下面看下核函数的定义
我的理解:这里的K(x)相当于一个球型的剖面,它确定了一个区域
下面我们来介绍两种核函数,高斯核函数:
这里的分母中的h,被称为带宽,不同带宽的核函数如下图所示:计算与画图代码如下:
import matplotlib.pyplot as plt
import math
def cal_Gaussian(x, h=1):
molecule = x * x #分子
denominator = 2 * h * h #分母
left = 1 / (math.sqrt(2 * math.pi) * h) # math.sqrt开根号,math.pi派
return left * math.exp(-molecule / denominator) # math.exp 对应 底数e
def basicPrinciple():
x = []
for i in range(-50, 50):
x.append(i * 0.5)
score_1 = []
scroe_2 = []
score_3 = []
score_4 = []
for i in x:
score_1.append(cal_Gaussian(i, 1))
scroe_2.append(cal_Gaussian(i, 2))
score_3.append(cal_Gaussian(i, 3))
score_4.append(cal_Gaussian(i, 4))
'''
print('score_1=', score_1)
print('scroe_2=', scroe_2)
print('score_3=', score_3)
print('score_4=', score_4)
'''
plt.figure()
plt.plot(x, score_1, color = 'blue', linestyle = '--', label = 'h = 1')
plt.plot(x, scroe_2, color = 'red', linestyle = '--', label = 'h = 2')
plt.plot(x, score_3, color = 'orange', linestyle = '--', label = 'h = 3')
plt.plot(x, score_4, color = 'yellow', linestyle = '--', label = 'h = 4')
plt.legend(loc="upper right")
plt.xlabel('x')
plt.ylabel('N')
plt.show()
return
def workSpace():
basicPrinciple()
return
workSpace()
可以看到h越大x的宽度越大
2 Mean Shift算法的核心算法原理与思想
Mean Shift算法和k-means相似,都是一个迭代的过程,即先算出当前点的偏移均值,将该点移动到该偏移均值,以此为新的起始点,继续移动,直到满足最终的条件。
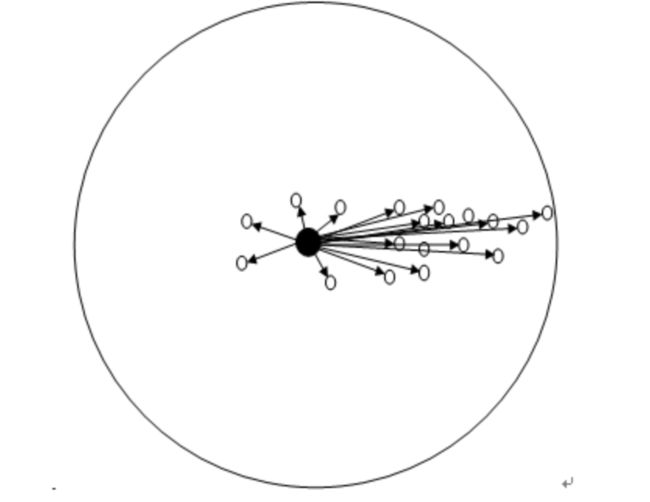
下面给了张物理方面的图示,来理解下:
这里的S(h)是一个半径为h的高维球区域,满足以下等式关系的y点的集合:
上面等式中的k值表示在这n个样本点x(i)中,有k个点落入S(h)区域,在上式中,我们可以看到(x(i) - x)是样本x(i)相对于点x的偏移向量,上面式子做的就是落入区域S(h)中的k个样本点相对于点x偏移向量求和然后再平均,那么如果样本点x(i)从一个概率密度函
数f(x)中采样得到,由于非零的概率密度梯度指向概率密度增大的最大的方向,因此从平均上来说,S(h)的样本点更多的是落在沿着概率密度梯度的方向,因此,对应的,
Mean Shift向量M(x)应该指向概率密度梯度的方向。
如上图所示,大圆圈所圈住的是S区域,小圆圈表示落入S区域的样本点x(i), 黑色的点就是Mean Shift的基准点x,箭头表示样本点相对于基准点x的偏移向量,很明显我们可以看出,平均的偏移M(x)会指向样本分布最多的区域,也就是概率密度函数梯度的方向。
注:这里,在上面式子中看到,只要是落入S区域的采样点,无论其离中心点x的远近,对最终M(x)的计算的贡献是一样的。然而在这个迭代的过程中,每个x(i)对于求解均值时的贡献是不同的,所以这里引入了其他类型的核函数。下面将下高斯核函数的方式。
3 用高斯核函数改进Mean Shift算法
把高斯核函数和样本权重加入M(x)的式子中,得到Mean Shift向量的新的形式:
把mh代入Mh则可以得到下列公式,正好印证了梯度上升的过程:
下面我们来看下高斯核函数是什么样子的:
式子中的H如上面这个矩阵。
二 以下是个应用的例子,demo
参考博客:http://blog.csdn.net/google19890102/article/details/51030884
https://www.cnblogs.com/ywsoftware/p/4434595.html