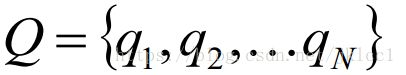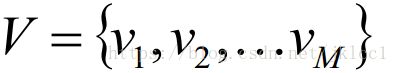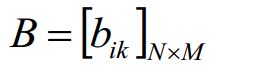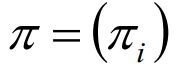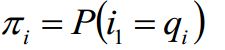隐马尔科夫模型HMM（一）HMM模型

隐马尔科夫模型HMM（一）HMM模型

一、概述

隐马尔可夫模型(HiddenMarkovModel，HMM)是统计模型，包含观察状态和帮助确定观察状态的隐藏状态。它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。（1）

一种HMM可以呈现为最简单的动态贝叶斯网络。在简单的马尔可夫模型(如马尔可夫链)，所述状态是直接可见的观察者，因此状态转移概率是唯一的参数。在隐马尔可夫模型中，状态是不直接可见的，但输出依赖于该状态下，是可见的。每个状态通过可能的输出记号有了可能的概率分布。因此，通过一个HMM产生标记序列提供了有关状态的一些序列的信息。（1）

二、使用范围

使用HMM模型时我们的问题一般有这两个特征：

１）我们的问题是基于序列的，比如时间序列，或者状态序列。（2）

２）问题中拥有可观测到的（观测序列）和不可观测到的（隐藏状态序列）两类数据。

三、HMM模型定义及两个重要假设

1.隐藏状态和观测状态

，所有可能的隐藏状态的集合，NN是可能的隐藏状态数

，是所有可能的观测状态的集合，MM是所有的可能的观察状态数

对于一个长度为TT的序列，II对应的状态序列, OO是对应的观察序列，即：

　　　　

其中，任意一个隐藏状态it∈Qit∈Q,任意一个观察状态ot∈V

2.两个重要假设

1）齐次马尔科夫链假设。即任意时刻的隐藏状态只依赖于它前一个隐藏状态。这样假设的好处就是模型简单，便于求解。

如果在时刻t的隐藏状态是it=qi,在时刻t+1的隐藏状态是it+1=qj,则从时刻t到时刻t+1的HMM状态转移概率aij可以表示为：

 　　　　

这样aij可以组成马尔科夫链的状态转移矩阵A:

所以，

2）观测独立性假设。即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态，这也是一个为了简化模型的假设。如果在时刻tt的隐藏状态是it=qj,而对应的观察状态为Ot=Vk,则该时刻观察状态Vk在隐藏状态qj下生成的概率为bj(K),满足：

　　　　

这样bj(k)bj(k)可以组成观测状态生成的概率矩阵BB:

　　　　

除此之外，我们需要一组在时t=1的隐藏状态概率分布Π:

所以：

3.HMM模型定义：

由于Π可由A、B决定，Π和A又可以决定B，所以HMM的模型可表示为：

四、三个基本问题

1、评估问题：前向-后向算法----动态规划

给定模型 λ = (A, B,π)和观测序列 O={o1,o2, o3 ...}，计算模型 λ下观测 O出现的概率 P(O| λ)

2、解码问题：Viterbi算法----动态规划

已知模型 λ = (A, B,π)和观测序列 O={o1,o2, o3 ...}，求给定观测序列条件概率 P(I| O， λ)最大的状态序列 I

3、学习问题：Baum-Welch算法----EM算法

已知观测序列O={o1, o2, o3...}，估计模型λ =(A, B, π)的参数，使得在该参数下该模型的观测序列P(O| λ)最大

五、参考资料

部分参考资料

1.https://baike.so.com/doc/5592314-5804914.html

2.http://www.cnblogs.com/pinard/p/6945257.html

3.https://blog.csdn.net/u012771351/article/details/53112280

ps：剩下的内容之后补充。