通俗易懂的KMP算法详解
1.BF算法
首先,简单介绍BF(简单的模式匹配法);
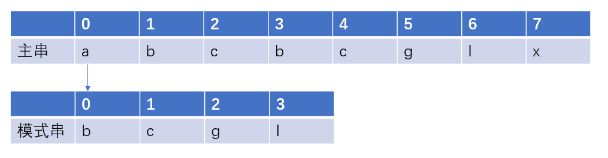
假设主串为“abcbcglx”长度为m, 模式串为"bcgl"长度为n。
通常先从主串的下标0开始与子串的下标0开始匹配,如果匹配失败,则从主串的第二个元素开始与子串的第一个元素进行匹配。
例如:第一次匹配:刚开始先用主串下标0‘a’与子串下标0‘a’开始匹配。匹配失败。
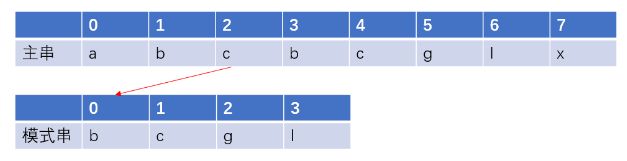
第二次匹配:从主串下标1‘b’开始与子串的下标0‘a’开始匹配。在红箭头处匹配失败。
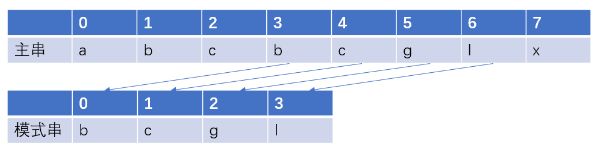
第三次匹配:接着从主串第三个元素即从主串下标2开始又重新从模式串下标0开始匹配。匹配失败。
第四次匹配:匹配成功。当子串完全匹配时,返回主串下标3。
当子串与主串匹配失败,即主串里无此子串,子串匹配失败,结果就会返回异常。在最不理想的情况下,时间复杂度为O(m*n),过高。
KMP是改进的BF。将时间复杂度从O(n*m)降到了O(n+m);
2.PTM
想要了解KMP,首先需要了解部分匹配表(PTM),这是KMP思想的核心。
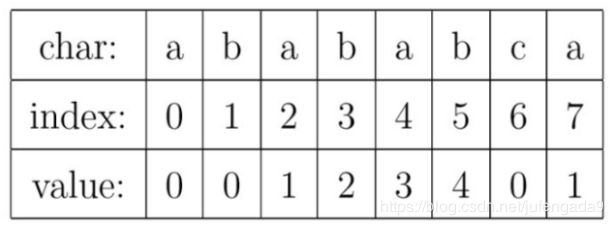
对于字串“abababca”表示如下:
首先,需要弄清前缀和后缀的意思。如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那么B就是A的前缀。例如,”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”},我们把所有前缀组成的集合,称为字符串的前缀集合。同样可以定义后缀A=SB, 其中S是任意的非空字符串,那就称B为A的后缀,例如,”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”},然后把所有后缀组成的集合,称为字符串的后缀集合。要注意的是,字符串本身并不是自己的后缀。
PTM中的值就是字符串的前缀集合与后缀集合的交集中最长元素的长度。
3.KMP
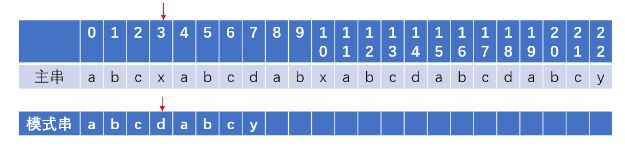
KMP算法的目的,主串无需从头重新匹配,需要判断的是,在子串中不匹配的字符串里面,是否有相同的前缀和后缀。例如:看下图,我们需要看的是在子串中d之前的字符串里是否有相同的前缀与后缀。‘abc’没有相同的前缀和后缀,所以下一次匹配时,子串需要回到开头,用‘a’于‘x’匹配。
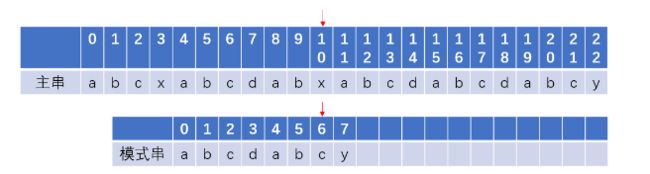
‘a’和‘x’不匹配,所以主串移动至下一字符‘a’开始与子串‘a’匹配。然而在主串下标10‘x’与模式串下标6‘c’的地方不匹配。回头看看是否存在前缀和后缀相等的情况。‘ab’即是前缀又是后缀,这意味着,既然x与c之前的字符串都是匹配的,所以在主串中x之前的字符串也一定是‘ab’。在下一次对比中主串可以跳过‘ab’,让主串‘x’和子串‘c’进行匹配,这样主串这无需从子串的开头开始匹配。
4.构建next数组
如果高效的判断子串是否有相同的前后缀呢:利用了ptm的思想,构建临时数组next。
需要构建临时数组next,用于记录后缀和前缀相同数。KMP算法的主要目的就是当不匹配时,主串无需从头重新匹配。在不匹配的地方看子串的前缀和后缀交集的最长长度,这样在主串不匹配的地方前面也有这样长度与子串开头相同的地方,这样就可以跳过相同部分,无需从头开始进行匹配。从子串前缀的下一个元素开始匹配就好,节省了复杂度。
KMP假设在模式串位置k上于主串位置m不匹配,假设前缀和后缀相同数目为n,k前面有n个与对应于m前面n个相同的字符,所以不用再比较它们。这样就能节省搜索。
KMP的时间复杂度为O(n+m)。因为假设主串长度为m,模式串长度为n,主串搜索的复杂度为O(m),模式串的临时数组next的复杂度为O(n);所以把他们相加就好。
参考:知乎文章:https://www.zhihu.com/question/21923021/answer/281346746
b站视频(超好视频!!一定要看!!看了就懂!!)https://www.bilibili.com/video/av3246487?from=search&seid=15687092047919541287