Unity3D引擎之渲染技术系列四

笔者介绍：姜雪伟，IT公司技术合伙人，IT高级讲师，CSDN社区专家，特邀编辑，畅销书作者，国家专利发明人;已出版书籍：《手把手教你架构3D游戏引擎》电子工业出版社和《Unity3D实战核心技术详解》电子工业出版社等。

CSDN视频网址：http://edu.csdn.net/lecturer/144

前面介绍了透视投影的矩阵计算，讲这些的目的是为了让读者真正领会各个空间的矩阵变换。我们自己在开发时，如果需要外在的矩阵传入，需要自己手动进行换算，这些就需要开发者对矩阵变换了解，接下来继续正交投影矩阵的计算。

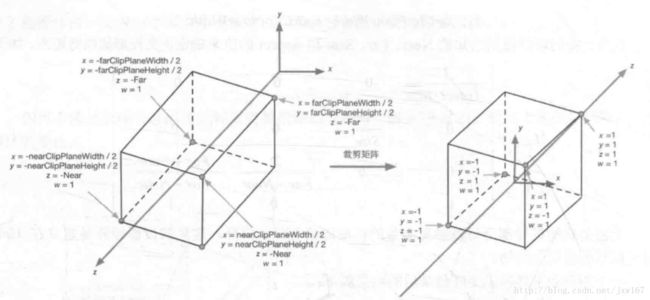
在Unity中功能正交投影中的6个裁剪面定义和透视投影类似，它们是由Camara组件中的参数和Game视图的横纵比共同决定的，如图所示：

正交投影的视锥体是一个长方体，因此计算上相比透视投影来说更加简单。由上图可以看出，通过Camera组件的Size属性来改变视锥体竖直方向上的高度的一半，而Clipping Planes中功能的Near和Far参数可以控制视锥体的近裁剪平面和远裁剪平面距离摄像机的远近。我们可以求出视锥体近裁剪面和远裁剪平面的高度，公式如下：

nearClipPlaneHeight=2*Size

farClipPlaneHeight=nearClipPlaneHeight

同样，我们还缺乏横向数据，我们可以通过摄像机的横纵比得到。假设当前摄像机的横纵比为Aspect，那么：

nearClipPlaneWidth＝Aspect*nearClipPlaneHeight.

farClipPlaneWidth=nearClipPlaneWidth

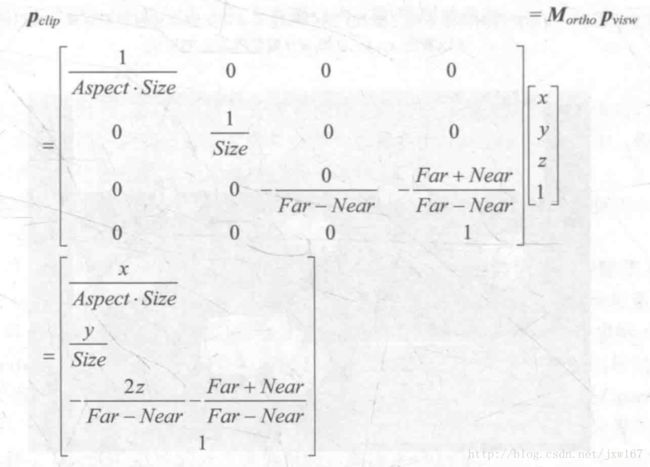
现在，我们可以通过已知的Near、Far、Size和Aspect的值来确定正交投影的裁剪矩阵。如下：

这里的投影矩阵时建立在Unity对坐标系的假定上面的，一个顶点和上述投影矩阵相乘后的结果如下：

细心的读者会注意到，和透视投影不同的是，使用正交投影的投影矩阵对顶点进行变换后，其w分量仍然为1，本质上是因为投影矩阵最后一行的不同，透视投影的投影矩阵最后一行是［0 0 －1 0］，而正交投影的投影矩阵的最后一行是［0 0 0 1］。这样的选择是有原因的，主要是为了齐次除法做准备，将在后面给读者介绍。

判断一个变换后的顶点时否位于视锥体内使用的不等式和透视投影中的一样，同样裁剪矩阵改变了空间的旋向性，经过正交投影变换后的顶点实际已经位于一个立方体内了。在前面博客中确定了模型的孩子在观察空间中的位置－（9，8.84，－27.31）。现在，我们要计算它在裁剪空间中的位置。

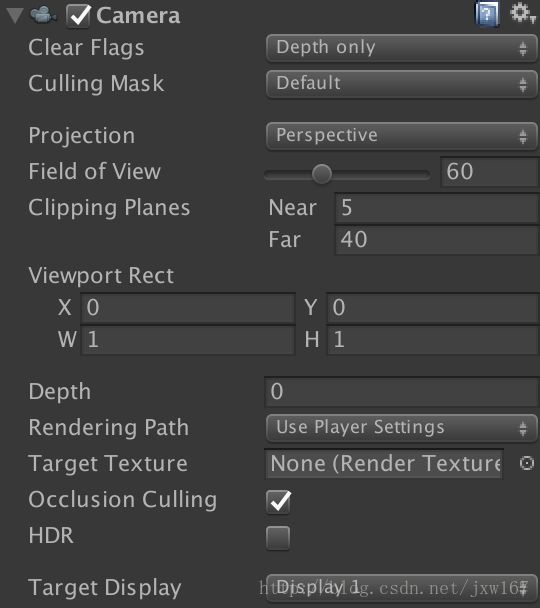
首先我们要确认使用的摄像机类型，场景中显示的是一个3D模型，因此使用透视摄像机，摄像机效果如下所示：

根据Unity提供的参数效果图如下所示：

我们可以通过透视投影参数：FOV为 60度，Near为5，Far为40，Aspect为4/3=1.333。对应的投影矩阵就是：

然后，我们用这个投影矩阵把模型的孩子从观察空间转换到裁剪空间中。如下：

这样，我们就求出了孩子在裁剪空间中的位置－（11.691，15.311，23.692，27.31）。最后，Unity会判断孩子是否需要裁剪。必须满足下面的不等式：

通过不等式可以看出，该孩子节点没有被裁减掉，在可视范围内。

给读者介绍矩阵实现原理的目的也是告诉读者，Unity3D引擎内部也是这样实现的，我们在开发产品时也会遇到这些运算，比如我们跟C＋＋封装的库接口进行对接，库函数提供矩阵给我们，那么我们必须用矩阵去运算，然后再将其转化成Transform组件下 的参数赋值给对象，让场景中的对象做出改变。后面给读者介绍屏幕空间。。。。。。。