2019第十届蓝桥杯省赛C/C++B组题解

作为很久很久没有写过算法题的考研狗 OvO（是这样的，卑微考研），我于今年再次参加了蓝桥杯...

大家都说这次蓝桥杯简单，我也是这么觉得的（或者说是我运气好），或者说是考细节吧（虽然我也没怎么考虑细节qwq），反正整个比赛的过程中心情感觉是放飞了自我（超级轻松）....

考完最开始在知乎上对了一波答案感觉凉的透彻，想着这次省三能不能拿到qwq，结果当成绩出来的时候是省一...名次貌似也还不错...这次抽空，想着马上就要国赛了，多多练习一下题目，也把这次的吃面包之旅好好总结一哈~~~~

爱心是卑微的博主的成绩（羞涩）

、

 

好了废话不多说，各位扁桃体同学，下面看博主开始发炎了（来看看题目有多水）~~~

一、组队

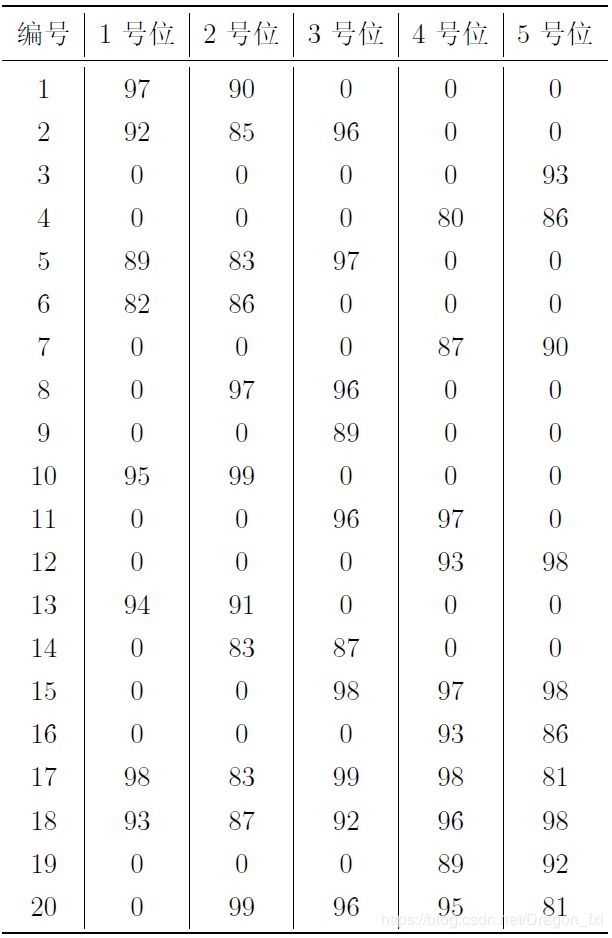
作为篮球队教练，你需要从以下名单中选出 1 号位至 5 号位各一名球员，组成球队的首发阵容。
每位球员担任 1 号位至 5 号位时的评分如下表所示。请你计算首发阵容 1 号位至 5 号位的评分之和最大可能是多少？

 

解答：最开始看到这题没看清楚题意差点坑了，直接把所有的最大值加起来了...还好感觉后来不对劲想了我去...这个只能出5名同学，我一看，应该是dfs，但是感觉第一题简单题啊我去，用啥dfs，直接目测一波。嗯，我就目测了一波。在纸上算了下，得出正确答案490。

答案: 490（注意不要算重复了）

 

二、年号字串

小明用字母A 对应数字1，B 对应2，以此类推，用Z 对应26。对于27以上的数字，小明用两位或更长位的字符串来对应，例如AA 对应27，AB 对应28，AZ 对应52，LQ 对应329。
请问2019 对应的字符串是什么？

解答：这题脑子都不想动....最开始我以为字符串要求是升序字符串才合法，但是从题意验证了一下发现BA这种也可以存在....然后疯狂暴力，直接用笔算（不就是找个规律么，代码都不想敲），10分钟左右算出结果为BYQ。

但是为了大家方便看过程，附上代码：

#include 
using namespace std;
//702 --> ZZ
//703 --> AAA
//18278 --> ZZZ
//18279 --> AAAA
void dfs(int N) {
    //并不是26进制哟
    if (N > 26) dfs((N - 1) / 26);
    putchar('A' + (N - 1) % 26);
}
int main() {
    int N;
    while (cin >> N) {
        dfs(N); cout << endl;
    }
    return 0;
}

答案: BYQ（注意...没啥注意的有问题验证题意就完事儿了）

 

三、数列求值

给定数列1, 1, 1, 3, 5, 9, 17, …，从第4 项开始，每项都是前3 项的和。求
第20190324 项的最后4 位数字。

解答：看到这个，很明显如果暴力直接加肯定会爆掉，注意是最后4位数字，也就是说前面无论怎么骚，关最后4位数啥事儿呢？比如148665468797436465+4678646456465465465求最后4位数，前面再怎么花里胡哨也没用吧qwq，我们只要求最后最后4位数相加就可以了，注意时刻对10000取模就完事儿了吧。

方法：打表取模。

#include
#include
using namespace std;
int main()
{
	int a=1,b=1,c=1;
	int ans;
	for(int i=4;i<=20190324;i++)
	{
		ans=(a+b+c)%10000;
		a=b%10000;
		b=c%10000;
		c=ans%10000;
	}
	cout<

答案：4659（注意取模）

 

四、数的分解

把2019 分解成3 个各不相同的正整数之和，并且要求每个正整数都不包含数字 2 和 4，一共有多少种不同的分解方法？
注意交换3个整数的顺序被视为同一种方法，例如1000+1001+18 和 1001+1000+18 被视为同一种。

解答：直接三重循环打表判断。

#include 
using namespace std;
bool isOK(int x) {
    for (/* */; x > 0; x /= 10)
        if (x % 10 == 2 || x % 10 == 4) return false;
    return true;
}
int main() {
    int N = 2019;
    int cnt = 0;
    for (int i = 1; i < N / 3; ++i)
        if (isOK(i))
            //k = N - i - j > j
            for (int j = i + 1; N - i - j > j; ++j)
                if (isOK(j) && isOK(N - i - j)) ++cnt;
    cout << cnt << endl;
    return 0;
}

答案: 40785

 

五、 迷宫

前面4题对了，第5题最后一点时间没dfs出来....最短路径长度很熟练了，标记我硬是不知道用dfs怎么去标记（好了我太菜我已经知道了）。

下图给出了一个迷宫的平面图，其中标记为1 的为障碍，标记为0 的为可以通行的地方。

010000
000100
001001
110000

迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这个它的上、下、左、右四个方向之一。
对于上面的迷宫，从入口开始，可以按DRRURRDDDR 的顺序通过迷宫，一共10 步。其中D、U、L、R 分别表示向下、向上、向左、向右走。对于下面这个更复杂的迷宫（30 行50 列），请找出一种通过迷宫的方式，其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。请注意在字典序中D

01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000

等我抽空敲一下再上代码。

 

六、特别数的和

小明对数位中含有 2、0、1、9 的数字很感兴趣（不包括前导0），在1 到 40 中这样的数包括1、2、9、10 至 32、39 和 40，共 28 个，他们的和是 574。请问，在 1 到n 中，所有这样的数的和是多少？

【输入格式】
输入一行包含两个整数n。

【输出格式】
输出一行，包含一个整数，表示满足条件的数的和。

【样例输入】
40

【样例输出】
574

【评测用例规模与约定】
对于20% 的评测用例，1≤n≤10 1 \leq n \leq 101≤n≤10。
对于50% 的评测用例，1≤n≤100 1 \leq n \leq 1001≤n≤100。
对于80% 的评测用例，1≤n≤1000 1 \leq n \leq 10001≤n≤1000。
对于所有评测用例，1≤n≤10000 1 \leq n \leq 100001≤n≤10000。

解答：无脑暴力枚举。

#include
#include
using namespace std;
bool judge(int n)
{
	while(n!=0)
	{
		int k=n%10;
		if(k==2||k==0||k==1||k==9)
		return true;
		
		n=n/10;
	}
	return false;
}
int main()
{
	int n;
	cin>>n;
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		if(judge(i))
		{
			ans+=i;
		}
	}
	cout<

 

明天继续更新