远心光学成像系统原理详解

目录

1 预备知识

1.1 光阑的概念

1.2 孔径光阑、入射光瞳、出射光瞳

1.3 主光线

1.4 光学系统的景深

1.5 远心光学系统

2 远心镜头详解

2.1 远心镜头分类

2.2 远心镜头的特点

2.2.1 放大倍率稳定性

2.2.2 远心度（远心斜率）

2.2.3 透视误差限制

2.3 远心镜头优缺点

参考资料

---

1 预备知识

1.1 光阑的概念

如下图所示，透镜的大小限制了A点发出的成像光束的孔径角，像面的大小限制成像范围，它们都是对光束的限制，称为光阑。

光阑：起限制成像光束作用的透光孔。

孔径光阑	限制轴上点成像光束中边缘光线的最大倾角（孔径角）
视场光阑	限制物平面或物空间能被系统成像的最大范围（视场）
渐晕光阑	限制物空间轴外点发出的、本来能通过上述两种光孔的成像光束
消杂光光阑	限制杂散光（从视场外射入系统，或由镜头内部的光学表面、金属表面及镜座内壁的反射和散射所产生）

光阑的位置

孔径光阑	随系统而异，目视光学系统要求孔阑或孔阑的像一定要在外面，以与眼瞳重合；远心光学系统要求孔阑在焦面上。其他无特殊要求的可以选择。
视场光阑	一般是在实像面或中间实像面上，也可以没有
渐晕光阑	位置可选择，以改善成像质量，与视场光阑二者必有其一
消杂光光阑	位置可选择，以达到限制杂散光的目的，也可以没有

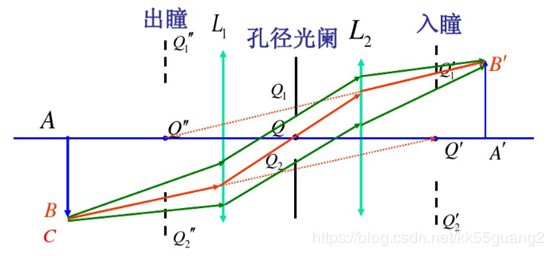
1.2 孔径光阑、入射光瞳、出射光瞳

孔径光阑：光学系统中，限制轴上点发出光束的孔径角的元件，简称孔阑，它决定了物体上各点有多大的光束可以进去光学系统。孔阑大小会影响成像亮度、景深等等

入射光瞳：孔阑通过其前面的透镜成像到物空间，这个像称为入射光瞳，简称入瞳。由光路的可逆性原理，物方光线直接被入瞳所限制，可以方便地画出物体能进入光线系统的光束，从而求得物方孔径角。

出射光瞳：孔阑通过其后面的透镜成像到像空间，这个像称为出射光瞳，简称出瞳。像方光线直接被出瞳所限制，可以方便地求得像方孔径角。

如何求孔阑：将所有光学系统中的所有元件通过其前面的元件成像到物空间，这些像对物面中心张角最小的那一个像为入瞳，对应的元件为孔阑，通过后面的元件成像到像空间，这个像为出瞳。

联系实际：

（1）相机中的光圈就是孔阑

（2）有很多目视光学系统在设计时，一般使出瞳与眼睛的瞳孔重合，如伽利略望远镜等

1.3 主光线

主光线：物点发出的通过孔阑中心的光线。

补充：其为参与成像的物光束的中心光线，故起名主光线。所有主光线均通过入瞳、孔阑、出瞳中心。

 

注：图中红线即为主光线。

1.4 光学系统的景深

景深：在景像平面上所获得的成清晰像的物空间深度。

                                     

理论上，只有共轭的物平面才能在像平面上成清晰像，其他物点所成的像均为弥散斑。但当此斑对眼睛的张角小于眼睛的最小分辨角1’ 时，人眼看起来仍为一点。此时，该弥散斑可认为是空间点在平面上的像。

如图，当Z1’和Z2’小到可以看成一点时，我们认为从B1到B2的空间深度范围内的物，都能在像平面上得到清晰像，这个空间深度叫景深。

注：图中A、A’平面分别为对准平面，景像平面。

1.5 远心光学系统

问题的提出：

 通过光学系统对AB成像测AB的长度，精确调焦可以精确测量。但如调焦不准（景深的影响），像面与分划板不重合，产生视差。

图(a)：调焦不准，如调焦于A1B1，在分划板上得弥散斑。量得的长度y1’比y’略短。反之若调焦于AB后，测得的长度略长。

 

图(b)：将孔径光阑放在像方焦面，物方主光线平行于光轴，调焦不准时只是看起来模糊些，弥散斑的中心不变，量得h准确。

远心光学系统：孔阑设于焦平面上的光学系统。

孔阑设于像方焦面，物方主光线平行于光轴，称物方远心光学系统。孔阑设于物方焦面，像方主光线平行于光轴，称像方远心光学系统。

命名由来：以物方远心光学系统为例，由于孔阑在物方焦平面处，其入瞳在物方无穷远处，入射光线看似来自无限远处，而心可能指入瞳中心，故称作“物方远心”。

2 远心镜头详解

2.1 远心镜头分类

远心镜头主要分为物方远心镜头、像方远心镜头和两侧远心镜头。

物方远心镜头

物方远心镜头是将孔径光阑放置在光学系统的像方焦平面上，当孔径光阑放在像方焦平面上时，即使物距发生改变，像距也发生改变，但像高并没有发生改变，即测得的物体尺寸不会变化。 物方远心镜头用于工业精密测量，畸变极小，高性能的可以达到无畸变。

像方远心镜头

像方远心镜头，通过在物方焦平面上放置孔径光阑，使像方主光线平行于光轴，从而虽然 CCD 芯片的安装位置有改变，在CCD 芯片上投影成像大小不变。

双远心镜头

双远心镜头兼于上面两种远心镜头的优点。在工业图像处理中，一般只使用物方远心镜头。偶尔也有使用两侧远心镜头的，（当然价格更高）。

2.2 远心镜头的特点

近年来，机器视觉技术在尺寸测量中的应用已经愈加流行：相机、软件和照明组件的进步使得达到甚至超越直接接触法和激光方法的精度成为可能。

除了图像处理问题之外，视觉系统设计者还必须考虑到常见的近心光学器件引起的几个限制测量应用精度和可重复性的因素：

• 物体位移导致的放大倍率变化
• 图像畸变
• 透视误差
• 较差的图像分辨率
• 光源几何形状导致的物体边缘位置的不确定性

远心镜头可以减少甚至消除以上大部分问题，因此它成为开发高精度测量应用的一个关键部件。

2.2.1 放大倍率稳定性

在测量应用中，经常需要用到物体的正交视图（即没有物侧成像），以便执行正确的线性测量。

此外，许多机械部件无法精确定位（例如，由于振动），或者必须在不同的深度或甚至更糟的情况下进行测量时，物体的厚度（进而物体表面的位置）可能会发生变化；然而即便如此，软件工程师依然需要成像尺寸与实际尺寸之间的完美对应。

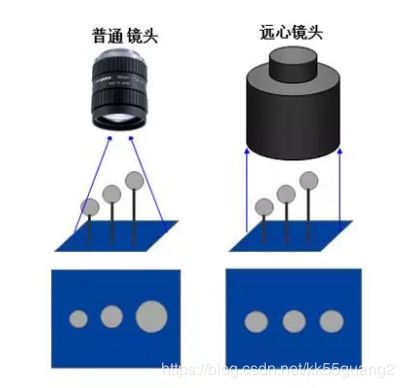
普通镜头在不同的共轭位置呈现不同的放大倍率：因此，当物体移动时，其图像大小的变化与物体到镜头的距离几乎成正比。任何人都可以在日常生活中轻松体验到这一点，例如使用配备有标准摄影镜头的相机拍照时。

 

当改变物体到镜头的距离 s 时，标准镜头会产生不同大小的图像。
另一方面，当具有相同视角时，不同大小的物体看起来具有相同的尺寸。

 

 

左：分别使用标准镜头（顶部）和远心镜头（底部）拍摄的圆柱形物体的内花键。
右：分别使用标准镜头（顶部）和远心镜头（底部）拍摄的两个完全相同的机器螺丝（间隔 100 mm ）。

2.2.2 远心度（远心斜率）

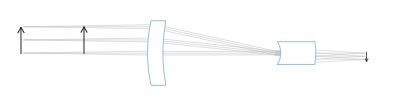
当物体保持在一定的范围内时，远心镜头获得的图像尺寸不会随物体位移而发生变化，这一范围通常被称为“景深”或“远心范围”。这是由于光线在光学系统内的特定路径而产生的：只有主光线平行于光轴时，才能被物镜捕获到。因此，前端镜头的直径至少要与物方视场对角线一样大。

这种光学行为通过将孔径光阑精确定位于前方光学组的焦平面上而获得：入射光瞄准看似来自于无限远处的入射光瞳。“telecentric”（远心的）这个词语来源于“tele”（古希腊语中的意思是“远的”）和“centre”（中心）（指的是瞳孔孔径——光学系统的实际中心）。​​​​​​​

在远心光学系统中，光线只能通过平行于光轴的路径进入光学器件。

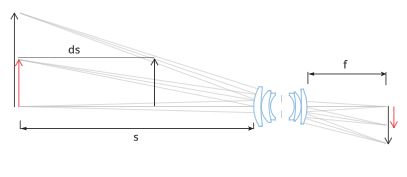
为了感受两种不同物镜的区别，我们设想一个标准镜头，焦距f = 12 mm，衔接一个1/3"的探测器，面对一个高度H = 20 mm、距离s = 200 mm的物体。

假设物体位移ds = 1mm，其尺寸的变化将大约为：

dH = (ds/s) · H = (1/200) · 20 mm = 0.1 mm

对于一个远心镜头，放大倍率的变化取决于“远心斜率”：好的远心镜头具有约为0.1°（0.0017弧度）的有效远心斜率θ；这意味着，物体位移ds为 1 mm时，其尺寸只会改变

dH = ds · theta= 1 · 0.0017 mm = 0.0017 mm

因此，相比于标准镜头，远心镜头放大倍率的误差减少到1/10至1/100。

远心斜率决定放大倍率的变化。

 

 

2.2.3 透视误差限制

当使用普通的光学器件对三维物体（非完全平坦的物体）成像时，远处物体看起来会比近处物体更小。因此，对一个圆柱空腔成像时，其顶冠和底冠边缘会呈现为两个同心圆，尽管实际上这两个圆是完全相同的。

相反，在使用远心镜头时，两个冠边缘是完全重叠的，底冠边缘因而被完全遮挡。

这种效应取决于光线的特定路径：在使用普通光学器件时，“平行”于主光轴的各种几何信息在探测器平面方向上也会具有分量，而使用远心镜头时完全没有这种垂直分量。

可以将一个普通镜头描述为一个数学函数，该函数建立起一个三维物体空间与二维探测器（图像）空间之间的对应关系，而远心镜头则建立一个二维——二维的对应关系，它不会展示被测物体的第三维度，因此成为剖面成像和尺寸测量的完美组件。

普通光学器件（左）将纵向几何信息投射到探测器上，而远心镜头没有。

2..2.4 不存在边缘位置不确定性

逆光拍摄物体时，往往很难确定其边缘的确切位置。因为在黑暗的背景下，物体边缘的亮像素往往会与暗像素重叠。此外，如果物体具有高度的三维形状，边界效应也会进一步限制测量精度；如下图所示，光线以一定的入射角掠过物体边缘，被其表面反射后依然会被镜头捕获。镜头由此会认为这些光线来自物体后方；结果部分图像片段可能消失，使得测量非常不精确且不稳定。

如果使用远心镜头，则会大大减少普通成像镜头存在的边界效应。

 

使用远心镜头可以有效限制这种效应：如果瞳孔孔径足够小，那么可以进入镜头的唯一反射光将是那些近于平行主光轴的光线。

由于这些光线受到非常小的偏差影响，因此物体表面对其的反射不会损害测量精度。

想要完全解决这些问题，可以将准直（也称为“远心”）照明器连接到远心镜头，并利用平行光源发散度处理好镜头孔径与视场的匹配。这样一来，来自照明器的所有光均由镜头收集并传送给探测器，同时可实现极高的信噪比和难以置信的低曝光时间。另一方面，只有“预期的”光线进入成像镜头，这样就不会出现边界问题了。

准直（远心）照明仅将预期光线投射到成像系统中。

2.3 远心镜头优缺点

优点：

• 消除透视误差
• 远心镜头畸变一般都很小
• 远心镜头的照明较好

缺点：

• 体积大，价格高
  • 为了收集远心光线，远心镜头前方的光学组件必须至少与物体的最大尺寸一样大，故相比于普通光学镜头，远心镜头更大、更重，也更昂贵。
• 孔阑较小，要达到好的成像亮度，曝光时间更长

参考资料

1. 张以谟. 应用光学(第3版)[M]. 电子工业出版社, 2008.
2. 《应用光学》网上课件. 浙江大学.
3. 光圈. 维基百科.
4. 光学系统中的光阑. 百度文库
5. 光学系统中的光阑和光束限制. 百度文库
6. 远心光学基础. 维视图像
7. 远心镜头教程. OPTO Engineering
8. BI-TELECENTRIC LENSES TUTORIAL Full Version. OPTO Engineering. youtube.
9. 远心镜头相关视频. OPTO Engineering. youku