SPH算法的理论和实践(1)
前段时间做了一个有关于SPH算法的项目,现在正好抽空把它写出来。SPH(Smoothed Particle Hydrodynamics)是光滑粒子流体动力学方法的意思,说白了就是用粒子模拟流体的流动效果。由于项目当中涉及到利用SPH算法实现多流体混溶模拟,所以下面我会写针对单流体模拟和多流体混溶模拟分别进行介绍,在介绍之前还是先看看做出来的最终效果吧。
效果预览
单流体模拟的效果:
多流体混溶模拟的效果:
针对上述多流体混溶模型,利用marching cube算法进行液面绘制之后的效果:
1单流体理论部分
SPH (Smoothed Particle Hydrodynamics)是光滑粒子流体动力学方法的缩写,是在近20多年来逐步发展起来的一种无网格方法。该方法的基本思想是将连续的流体用相互作用的粒子来描述,各个粒子上承载各种物理量,包括质量、速度等,通过求解粒子的动力学方程和跟踪每个粒子的运动轨道,求得整个系统的力学行为。
1.1粒子受力分析
SPH方法具体的数学公式可以看这篇文章,里面介绍的很详细,我当时也是看这篇文章入门的。不过在这里我还是简单介绍一下里面的几个基本公式:
SPH算法的基本思想,就是将连续的流体想象成一个个相互作用的粒子,这些粒子相互影响,共同形成了复杂的流体运动。
所以,该算法最关键的就是如何求解粒子的运动?我们通过对粒子进行受力分析,利用牛顿第二定理![]() ,只要知道了粒子的受力,粒子的加速度自然就知道了,这样就可以跟踪粒子的运动,进而模拟出整个流体的动态效果。 那如何求解粒子的力F 呢?
,只要知道了粒子的受力,粒子的加速度自然就知道了,这样就可以跟踪粒子的运动,进而模拟出整个流体的动态效果。 那如何求解粒子的力F 呢?
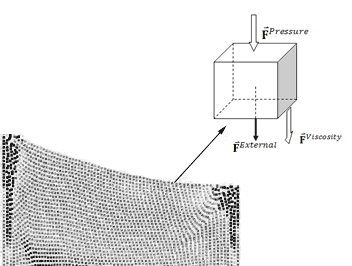
根据流体动力学,作用在粒子上的力由三部分组成:
其中,![]() 表示外力,一般就是重力
表示外力,一般就是重力
注意:这里的力F的量纲发生了变化,正常情况下,F=m*g。但在SPH算法里,流体的质量是由流体单元的密度决定的,所以一般用密度代替质量,后面的分析都是用这个量纲的“作用力”
![]() 表示压力,是由流体内部的压力差产生的作用力,试想一下在水管中流动的液体,进水口区域的压力一定会比出水口区域大,所以液体才会源源不断的流动,数值上,它等于压力场的梯度,方向由压力高的区域指向压力低的区域
表示压力,是由流体内部的压力差产生的作用力,试想一下在水管中流动的液体,进水口区域的压力一定会比出水口区域大,所以液体才会源源不断的流动,数值上,它等于压力场的梯度,方向由压力高的区域指向压力低的区域
![]() 表示粘滞力,是由粒子之间的速度差引起的,设想在流动的液体内部,快速流动的部分会施加类似于剪切力的作用力到速度慢的部分,这个力的大小跟流体的粘度系数μ以及速度差有关
表示粘滞力,是由粒子之间的速度差引起的,设想在流动的液体内部,快速流动的部分会施加类似于剪切力的作用力到速度慢的部分,这个力的大小跟流体的粘度系数μ以及速度差有关
所以,最后得到粒子的受力公式
加速度形式:
至此,我们基本搞清楚了粒子的运动学计算方法。下面介绍SPH算法的关键部分,如何通过光滑核函数求解上述公式
1.2光滑核函数
和其他流体力学中的数学方法类似,SPH算法同样涉及到“光滑核”的概念,可以这样理解这个概念,粒子的属性都会“扩散”到周围,并且随着距离的增加影响逐渐变小,这种随着距离而衰减的函数被称为“光滑核”函数,最大影响半径为“光滑核半径”。
反过来不难理解,尽管我们将流体视为一个个分散的粒子,但流体毕竟是连续充满整个空间的,流体中每个位置参与运算的值都是由周围一组粒子累加起来的。
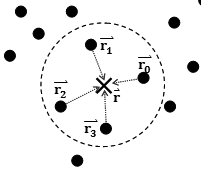
设想流体中某点 r⃗ r → (此处不一定有粒子),在光滑核半径h范围内有数个粒子,位置分别是 r⃗ 0,r⃗ 1,r⃗ 2,...,r⃗ j r → 0 , r → 1 , r → 2 , . . . , r → j ,则该处某项属性A的累加公式为:
其中 A⃗ j A → j 是要累加的某种属性, mj m j 和 ρj ρ j 是周围粒子的质量和密度, r⃗ r → 是该粒子的位置, h h 是光滑核半径。函数 W W 就是光滑核函数。
光滑核函数两个重要属性,首先一定是偶函数,也就是 W(−r)=W(r) W ( − r ) = W ( r ) ,第二,是“规整函数”,也就是 ∫W(r)dr=1 ∫ W ( r ) d r = 1
SPH推导过程
假设流体中的一个粒子 r⃗ i r → i ,假设它的压力为 ρ(ri) ρ ( r i ) ,密度为 p(ri) p ( r i ) ,速度为 u⃗ (ri) u → ( r i ) ,name我们可以根据上一节公式,得到该粒子的加速度 a⃗ (ri) a → ( r i ) :
对于SPH算法来说,基本流程就是这样,根据光滑核函数逐个推出流体中某点的密度,压力,速度相关的累加函数,进而推导出此处的加速度,从而模拟流体的运动趋势。
下面我们直接利用光滑核函数求解某点的密度,压力,速度的公式,具体的数学推导可以看这里。
密度
根据光滑核函数,用密度 ρ ρ 代替 A A ,可以得到
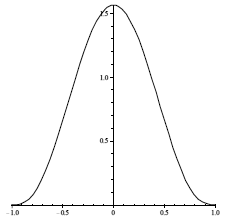
利用Poly6函数得到
压强
对于单个粒子的压力 p p 可以利用理想气体状态方程计算
其中 ρ0 ρ 0 是流体的静态密度, K K 是和流体相关的常数,只跟温度有关。
压力
根据光滑核函数,用压力 p p 代替 A A ,可以得到
利用Spiky函数,得到
其中 r=|r⃗ i−r⃗ j| r = | r → i − r → j |
粘滞力
根据光滑核函数,可以得到
根据viscosity函数,得到
其中 r=|r⃗ i−r⃗ j| r = | r → i − r → j |
其中 r=|r⃗ i−r⃗ j| r = | r → i − r → j |
OK,我们终于推导除了粒子加速度 a⃗ (ri) a → ( r i ) 的计算公式。那如何让这些公式在代码里跑起来呢?不用担心,这就是下一章我们要解决的问题了。